2022-2023学年江苏省苏州市高新实验初级中学八年级（下）月考数学试卷（3月份）（含解析）

这是一份2022-2023学年江苏省苏州市高新实验初级中学八年级（下）月考数学试卷（3月份）（含解析），共28页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。

2022-2023学年江苏省苏州市高新实验初级中学八年级（下）月考数学试卷（3月份）
一、选择题（本大题共10小题，共20.0分。在每小题列出的选项中，选出符合题目的一项）
1. 下列电视台标志中，是中心对称图形的是(    )
A. B. C. D.
2. 下列调查适合做普查的是(    )
A. 了解全国九年级学生身高的现状
B. 了解一批灯泡的平均使用寿命
C. 了解全球人类男女比例情况
D. 对患新型冠状病毒患者同一车厢的乘客进行医学检查
3. 一个不透明的袋子中只有4个黑球和2个白球，这些球除颜色外无其他差别，随机从袋子中一次摸出3个球，下列事件是必然事件的是(    )
A. 3个球都是黑球 B. 3个球都是白球 C. 3个球中有黑球 D. 3个球中有白球
4. 在如图4×4的正方形网格中，△MNP绕某点旋转一定的角度，得到△M1N1P1，则其旋转中心可能是(    )

A. 点A B. 点B C. 点C D. 点D
5. 平行四边形的对角线长为x，y，一边长为12，则x，y的值可能是(    )
A. 8和14 B. 10和14 C. 18和20 D. 10和34
6. 矩形具有而菱形不具有的性质是(    )
A. 对边平行且相等 B. 对角线互相平分 C. 对角线互相垂直 D. 对角线相等
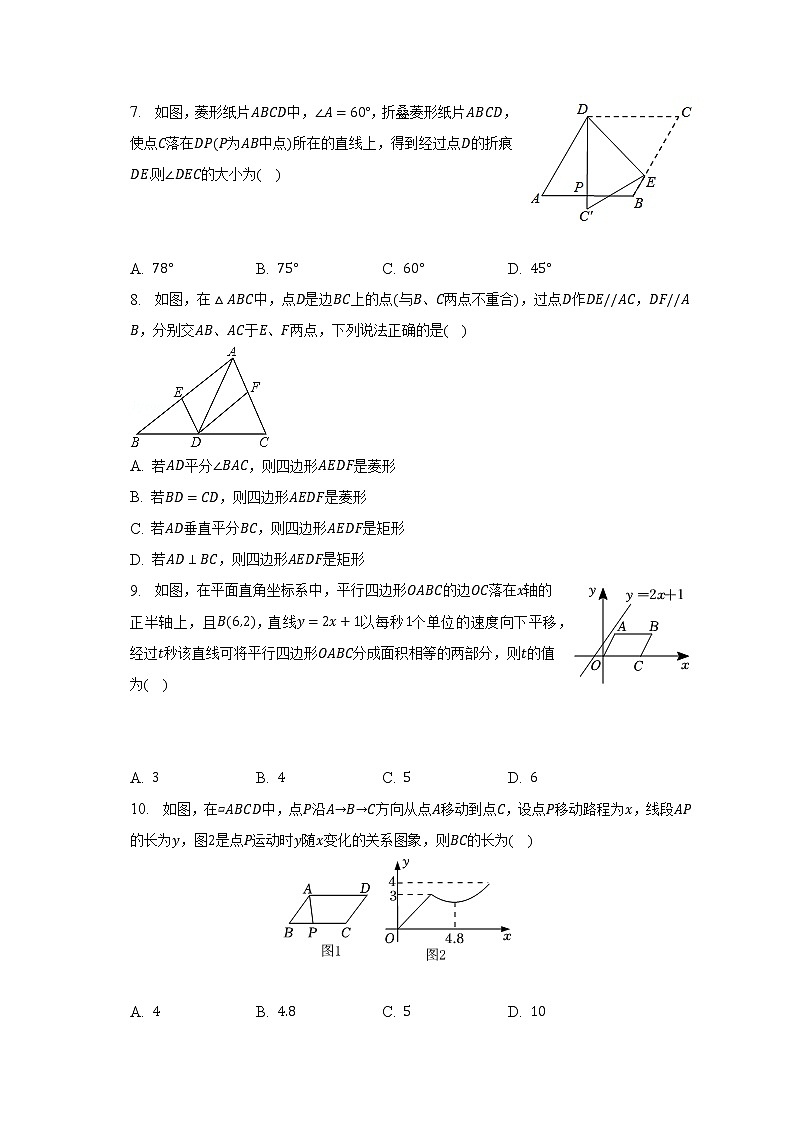
7. 如图，菱形纸片ABCD中，∠A=60°，折叠菱形纸片ABCD，使点C落在DP(P为AB中点)所在的直线上，得到经过点D的折痕DE.则∠DEC的大小为(    )


A. 78° B. 75° C. 60° D. 45°
8. 如图，在△ABC中，点D是边BC上的点(与B、C两点不重合)，过点D作DE//AC，DF//AB，分别交AB、AC于E、F两点，下列说法正确的是(    )

A. 若AD平分∠BAC，则四边形AEDF是菱形
B. 若BD=CD，则四边形AEDF是菱形
C. 若AD垂直平分BC，则四边形AEDF是矩形
D. 若AD⊥BC，则四边形AEDF是矩形
9. 如图，在平面直角坐标系中，平行四边形OABC的边OC落在x轴的正半轴上，且B(6,2)，直线y=2x+1以每秒1个单位的速度向下平移，经过t秒该直线可将平行四边形OABC分成面积相等的两部分，则t的值为(    )


A. 3 B. 4 C. 5 D. 6
10. 如图，在▱ABCD中，点P沿A→B→C方向从点A移动到点C，设点P移动路程为x，线段AP的长为y，图2是点P运动时y随x变化的关系图象，则BC的长为(    )

A. 4 B. 4.8 C. 5 D. 10
二、填空题（本大题共8小题，共24.0分）
11. 平行四边形ABCD中，∠A+∠C=100°，则∠B=______度．
12. 为了了解某校2022年960名学生中考数学学科学科各分数段成绩分布情况，从中抽取120名考生的数学成绩进行统计分析，本次调查的样本是：        ．
13. 某校有40人参加全国数学竞赛，把他们的成绩分为6组，第一至第四组的频数分别为10，5，7，6，第五组的频率是0.20.则第六组的频率是______．
14. 菱形的边长为5，一条对角线长为8，则其面积为______ ．
15. 如图，平行四边形ABCD中，对角线AC，BD相交于点O，OE⊥BD交AD于点E，连接BE，若平行四边形ABCD的周长为28，则△ABE的周长为______．

16. 如图，矩形ABCD绕点A逆时针旋转α(0°<α<90°)得到矩形AB′C′D′，此时点B′恰好在DC边上，若∠CBB′=15°，则α的大小为        ．


17. 如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，P为AB边上不与A、B重合的一动点，过点P分别作PE⊥AC于点E，PF⊥BC于点F，则线段EF的最小值是          ．



18. 在矩形纸片ABCD中，AB=8，BC=20，F为BC的中点，沿过点F的直线翻折，使点B落在边AD上，折痕交矩形的一边于G，则折痕FG= ______ ．
三、计算题（本大题共1小题，共6.0分）
19. 某工人为一客户制作一长方形防盗窗，为了牢固和美观，设计如图所示，中间为三个菱形，其中左右为两个全等的大菱形，中间为一个小菱形，竖着的铁棍的间距是相等的，尺寸如图所示(单位：m)，工人师傅要做这样的一个防盗窗，总共需要多长的铁棍．(不计损耗)



四、解答题（本大题共9小题，共50.0分。解答应写出文字说明，证明过程或演算步骤）
20. (本小题4.0分)
在一个不透明的盒子里装有黑、白两种颜色的球共100只，这些球除颜色外其余完全相同．小颖做摸球实验，搅匀后，她从盒子里随机摸出一只球记下颜色后，再把球放回盒子中，不断重复上述过程，如表是实验中的一组统计数据：
摸球的次数n
100
200
300
500
800
1000
3000
摸到白球的次数m
70
124
190
325
538
670
2004
摸到白球的频率mn
0.70
0.62
0.633
0.65
0.6725
0.670
0.668
(1)若从盒子里随机摸岀一只球，则摸到白球的概率的估计值为______；(精确到0.01)
(2)试估算盒子里黑球有______只；
(3)某小组在“用频率估计概率”的试验中，符合这一结果的试验最有可能的是______.A.从一副扑克牌中任意抽取一张，这张牌是“红色的”B.掷一枚质地均匀的硬币，落地时结果是“正面朝上”C.掷一个质地均匀的正六面体骰子(面的点数标记分别为1到6)，落地时面朝上的点数小于5．
21. (本小题4.0分)
某单位食堂为全体960名职工提供了A，B，C，D四种套餐，为了解职工对这四种套餐的喜好情况，单位随机抽取240名职工进行“你最喜欢哪一种套餐(必选且只选一种)”问卷调查，根据调查结果绘制了条形统计图和扇形统计图，部分信息如下：

(1)在抽取的240人中最喜欢A套餐的人数为        ；扇形统计图中“C”对应扇形的圆心角的大小为        ．
(2)依据本次调查的结果，估计全体960名职工中最喜欢B套餐的人数．
22. (本小题6.0分)
如图，在边长为1个单位长度的小正方形组成的网格中，△ABC的顶点均在格点上，点A的坐标为(2,3)，点B的坐标为(3,0)，点C的坐标为(0,2)．
(1)以点C为旋转中心，将△ABC旋转180°后得到△A1B1C1，请画出△A1B1C1；
(2)平移△ABC，使点A的对应点A2的坐标为(0,−1)，请画出△A2B2C2．
(3)若将△A1B1C1绕点P旋转可得到△A2B2C2，则点P的坐标为

23. (本小题6.0分)
如图，平行四边形ABCD的周长为36cm，由钝角顶点D向AB、BC引两条高DE、DF，且DE=4cm，DF=5cm．
(1)猜想：∠1与∠B的大小关系，并说明理由；
(2)求这个平行四边形的面积．

24. (本小题6.0分)
如图，在正方形ABCD中，E为AB上一点，仅用无刻度的直尺作图，保留作图痕迹．
(1)在AD上找点M，使AM=AE；
(2)在CD上找点F，使BF=DE．

25. (本小题6.0分)
如图，在矩形ABCD中，对角线AC的垂直平分线EF分别交AD、AC、BC于点E、O、F，连接CE和AF．
(1)求证：四边形AECF为菱形；
(2)若AB=4，BC=8，求菱形AECF的周长．

26. (本小题6.0分)
如图，四边形ABCD是边长为4的正方形，点E、F依次为AD、CD边上的动点，且分别从A、D出发，以相同的速度同时向终点D、C运动，连接BE、AF相交于H．
(1)试问：在整个运动过程中，BE、AF之间的关系是否保持不变，并请说明理由；
(2)AB的中点为G，在整个运动过程中，是否存在某一时刻.使DH+HG=2+22，若存在，请举例说明；若不存在，请说明理由理由．

27. (本小题6.0分)
如图，Rt△ABC中，∠ACB=90°，AC=BC，D为CA上一动点，E为BC延长线上的动点，始终保持CE=CD，连接BD和AE，再将AE绕A点逆时针旋转90°到AF，再连接DF．

(1)求证：△BCD≌△ACE；
(2)判断四边形ABDF的形状并证明；
(3)如图2，连接EF，G为EF中点，BC=4，当D从C运动到A点的过程中，EF的中点G也随之运动，请直接写出G点所经过的路径长．
28. (本小题6.0分)
已知矩形ABCD，AB=6，BC=10，以BC所在直线为x轴，AB所在直线为y轴，建立如图所示的平面直角坐标系，在CD边上取一点E，将△ADE沿AE翻折，点D恰好落在BC边上的点F处．
(1)求线段EF长；
(2)在平面内找一点G，
①使得以A、B、F、G为顶点的四边形是平行四边形，请直接写出点G的坐标；
②如图2，将图1翻折后的矩形沿y轴正半轴向上平移m个单位，若四边形AOGF为菱形，请求出m的值并写出点G的坐标．

答案和解析

1.【答案】B 
【解析】解：A、不是中心对称图形，故本选项错误；
B、是中心对称图形，故本选项正确；
C、不是中心对称图形，故本选项错误；
D、不是中心对称图形，故本选项错误．
故选：B．
根据中心对称图形的概念对各选项分析判断即可得解．
本题考查了中心对称图形的概念，中心对称图形是要寻找对称中心，旋转180度后两部分重合．

2.【答案】D 
【解析】解：A、了解全国九年级学生身高的现状，适合抽样调查，故本选项不合题意；
B、了解一批灯泡的平均使用寿命，适合抽样调查，故本选项不合题意；
C、了解全球人类男女比例情况，适合抽样调查，故本选项不合题意；
D、对患新型冠状病毒患者同一车厢的乘客进行医学检查，适合普查，故本选项符合题意；
故选：D．
由普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果比较近似．
本题考查了抽样调查和全面调查的区别，选择普查还是抽样调查要根据所要考查的对象的特征灵活选用，一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查．

3.【答案】C 
【解析】解：一个不透明的袋子中只有4个黑球和2个白球，这些球除颜色外无其他差别，随机从袋子中一次摸出3个球，
A、3个球都是黑球，是随机事件，故本选项不符合题意；
B、3个球都是白球，是不可能事件，故本选项不符合题意；
C、3个球中有黑球，是必然事件，故本选项符合题意；
D、3个球中有白球，是随机事件，故本选项不符合题意；
故选：C．
根据事件发生的可能性大小判断相应事件的类型即可．
本题考查的是必然事件、不可能事件、随机事件的概念．必然事件指在一定条件下，一定发生的事件．不可能事件是指在一定条件下，一定不发生的事件，不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．

4.【答案】B 
【解析】
【分析】
本题考查了学生的理解能力和观察图形的能力，重点掌握旋转的性质，注意：旋转时，对应顶点到旋转中心的距离应相等且旋转角也相等，对称中心在连接对应点线段的垂直平分线上．
连接PP1、NN1、MM1，分别作PP1、NN1、MM1的垂直平分线，看看三线都过哪个点，那个点就是旋转中心．
【解答】
解：∵△MNP绕某点旋转一定的角度，得到△M1N1P1，
∴连接PP1、NN1、MM1，

作PP1的垂直平分线过B、D、C，
作NN1的垂直平分线过B、A，
作MM1的垂直平分线过B，
∴三条线段的垂直平分线正好都过B，
即旋转中心是B．
故选：B．  
5.【答案】C 
【解析】解：A、82+142=4+7=11<12，所以不可能；
B、102+142=5+7=12=12，所以不可能；
D、34−10=24，所以不可能；
故选：C．
如图：因为平行四边形的对角线互相平分，所OB=y2，OC=x2，在△OBC中任意两边之和大于第三边，任意两边之差小于第三边，将各答案代入验证即可求得．
即x+y>24，y−x<24．
本题考查平行四边形的性质以及三角形的三边关系定理．

6.【答案】D 
【解析】解：∵矩形的性质为对边平行且相等，对角线相等且互相平分，菱形的性质为对边平行且相等，对角线互相垂直平分，
∴矩形具有而菱形不具有的性质是对角线相等，
故选：D．
利用矩形的性质和菱形的性质可直接求解．
本题考查了矩形的性质，菱形的性质，掌握特殊四边形的性质是解题的关键．

7.【答案】B 
【解析】解：连接BD，
∵四边形ABCD为菱形，∠A=60°，
∴△ABD为等边三角形，∠ADC=120°，∠C=60°，
∵P为AB的中点，
∴DP为∠ADB的平分线，即∠ADP=∠BDP=30°，
∴∠PDC=90°，
∴由折叠的性质得到∠CDE=∠PDE=45°，
在△DEC中，∠DEC=180°−(∠CDE+∠C)=75°．
故选：B．
连接BD，由菱形的性质及∠A=60°，得到三角形ABD为等边三角形，P为AB的中点，利用三线合一得到DP为角平分线，得到∠ADP=30°，∠ADC=120°，∠C=60°，进而求出∠PDC=90°，由折叠的性质得到∠CDE=∠PDE=45°，利用三角形的内角和定理即可求出所求角的度数．
此题考查了翻折变换(折叠问题)，菱形的性质，等边三角形的性质，以及内角和定理，熟练掌握折叠的性质是解本题的关键．

8.【答案】A 
【解析】解：A、若AD平分∠BAC，则四边形AEDF是菱形；正确；
B、若BD=CD，则四边形AEDF是平行四边形，不一定是菱形；错误；
C、若AD垂直平分BC，则四边形AEDF是菱形，不一定是矩形；错误；
D、若AD⊥BC，则四边形AEDF是平行四边形，不一定是矩形；错误；
故选：A．
由矩形的判定和菱形的判定即可得出结论．
本题考查了矩形的判定、菱形的判定；熟记菱形和矩形的判定方法是解决问题的关键．

9.【答案】D 
【解析】解：连接AC、BO，交于点D，当y=2x+1经过D点时，该直线可将▱OABC的面积平分；
∵四边形AOCB是平行四边形，
∴BD=OD，
∵B(6,2)，点C(4,0)，
∴D(3,1)，
设DE的解析式为y=kx+b，
∵平行于y=2x+1，
∴k=2，
∵过D(3,1)，
∴DE的解析式为y=2x−5，
∴直线y=2x+1要向下平移6个单位，
∴时间为6秒，
故选：D．
依题意，直线经过平行四边形对角线的交点时，平分平行四边形的面积，求出对角线交点坐标，进而根据一次函数平移的性质即可求解．
本题考查了一次函数的平移，平行四边形的性质，掌握平行四边形的中心对称性质，直线经过对角线的交点是解题的关键．

10.【答案】C 
【解析】解：如图：

根据图2知：当点P与点B重合时，AP=AB=3，
当AP⊥BC时，AB+BP=4.8，
∴BP=BE=1.8，
∴AE=AB2−BE2=32−1．82=125，
当点P到达点C时，AP=AC=4，
∴EC=AC2−AE2=42−(125)2=165，
∴BC=BE+EC=1.8+165=5．
故选：C．
根据平行四边形的性质，再结合P运动时y随x的变化的关系图象，通过勾股定理即可求解．
本题主要考查动点问题的函数图象，平行四边形的性质，勾股定理，掌握平行四边形的性质，根据点P运动规律，结合函数图象解题是解题关键．

11.【答案】130 
【解析】解：∵四边形ABCD为平行四边形，
∴∠A=∠C，又∠A+∠C=100°，
∴∠A=∠C=50°，
又∵AD//BC，
∴∠B+∠A=180°，
∴∠B=180°−∠A=180°−50°=130°．
故答案为130
根据平行四边形的性质可得∠A=∠C，又有∠A+∠C=100°，可求∠A=∠C=50°.又因为平行四边形的邻角互补，所以，∠B+∠A=180°，可求∠B．
此题主要考查：平行四边形的两组对角分别相等，平行四边形的邻角互补．

12.【答案】抽取的120名考生的数学成绩 
【解析】解：为了了解某校2022年960名学生中考数学学科学科各分数段成绩分布情况，从中抽取120名考生的数学成绩进行统计分析，
在这个问题中，样本是指从中抽取的120名考生的数学成绩．
故答案为：抽取的120名考生的数学成绩．
根据样本的定义：在抽样调查中，被抽取的那些个体组成了一个样本，即可得出答案．
本题考查了样本的定义．准确理解总体、个体、样本、样本容量是解题的关键．

13.【答案】0.1 
【解析】解：由题意得：
40×0.2=8，
∴第五组的频数是8，
∴40−10−5−7−6−8=4，
∴4÷40=0.1，
∴第六组的频率是：0.1，
故答案为：0.1．
先求出第五组的频数是8，从而求出第六组的频数，最后求出第六组的频率即可解答．
本题考查了频率与频数，熟练掌握频率等于频数÷总次数是解题的关键．

14.【答案】24 
【解析】解：：∵菱形的边长为5，一条对角线长为8，
∴另一条对角线的长为：252−42=6，
面积为12×6×8=24，
故答案为：24．
菱形的对角线互相垂直平分，四边相等，可求出另一条对角线的长，菱形的面积等于对角线乘积的一半．
本题考查菱形的性质，属于基础题，关键是掌握菱形的四边相等，对角线互相垂直平分，以及菱形面积等于对角线乘积的一半等知识点．

15.【答案】14 
【解析】解：∵四边形ABCD是平行四边形，
∴OB=OD，AB=CD，AD=BC，
∵▱ABCD的周长为28，
∴AB+AD=14
∵OE⊥BD，
∴OE是线段BD的中垂线，
∴BE=ED，
∴△ABE的周长=AB+BE+AE=AB+AD=14，
故答案为：14．
先判断出EO是BD的中垂线，得出BE=ED，从而可得出△ABE的周长=AB+AD，再由▱ABCD的周长为28，即可得出答案．
此题考查了平行四边形的性质及线段的中垂线的性质，解答本题的关键是判断出OE是线段BD的中垂线．

16.【答案】30° 
【解析】解：如图所示，连接BB′．

∵四边形ABCD是矩形，
∴∠ABC=90°，
∵∠CBB′=15°，
∴∠ABB′=90°−15°=75°，
∵AB=AB′，
∴∠ABB′=∠AB′B=75°，
∴∠BAB′=180°−2×75°=30°，
即α=30°，
故答案为：30°．
由矩形的性质，可知∠ABC=90°，再由旋转，可知△ABB′为等腰三角形，根据内角和求解即可．
本题考查旋转的性质，矩形的性质，等腰三角形的性质等知识，掌握性质的性质是解题的关键．

17.【答案】4.8 
【解析】解：如图，连接CP，
∵∠C=90°，AC=6，BC=8，
∴AB=AC2+BC2=62+82=10，
∵PE⊥AC，PF⊥BC，∠C=90°，
∴四边形CFPE是矩形，
∴EF=CP，
由垂线段最短可得CP⊥AB时，线段CP的值最小，即线段EF的值最小，
此时S△ABC=12BC·AC=12AB·CP，
∴12×8×6=12×10·CP，
解得CP=4.8，即EF的最小值为4.8．
故答案为4.8．
本题考查矩形的判定与性质，垂线段最短，以及勾股定理．
连接CP，利用勾股定理求出AB，判断出四边形CFPE是矩形，根据矩形的对角线相等可得EF=CP，再根据垂线段最短可得CP⊥AB时，线段EF的值最小，然后根据三角形的面积公式列出方程求解即可．

18.【答案】55或45 
【解析】解：分两种情况考虑：
(i)如图1所示，过F作FE⊥AD于E，G在AB上，B′落在AE上，可得四边形ABFE为矩形，
∴EF=AB=8，AE=BF，
又BC=20，F为BC的中点，
∴由折叠可得：B′F=BF=12BC=10，
在Rt△EFB′中，根据勾股定理得：B′E=B′F2−EF2=6，
∴AB′=AE−B′E=10−6=4，
设AG=x，则有GB′=GB=8−x，
在Rt△AGB′中，根据勾股定理得：GB′2=AG2+AB′2，
即(8−x)2=x2+42，
解得：x=3，
∴GB=8−3=5，
在Rt△GBF中，根据勾股定理得：GF=GB2+BF2=55；


(ii)如图2所示，过F作FE⊥AD于E，G在AE上，B′落在ED上，可得四边形ABFE为矩形，
∴EF=AB=8，AE=BF，
又BC=20，F为BC的中点，
∴由折叠可得：B′F=BF=12BC=10，
在Rt△EFB′中，根据勾股定理得：B′E=B′F2−EF2=6，
∴AB′=AE+B′E=10+6=16，
设AG=A′G=y，则GB′=AB′−AG=AE+EB′−AG=16−y，A′B′=AB=8，
在Rt△A′B′G中，根据勾股定理得：A′G2+A′B′2=GB′2，
即y2+82=(16−y)2，
解得：y=6，
∴AG=6，
∴GE=AE−AG=10−6=4，
在Rt△GEF中，根据勾股定理得：GF=GE2+EF2=45，
综上，折痕FG=55或45．
故答案为：55或45．
过F作FE⊥AD于E，可得出四边形ABFE为矩形，利用矩形的性质得到AE=BF，AB=EF，分两种情况考虑：(i)当G在AB上，B′落在AE上时，如图1所示，由折叠的性质得到B′F=BF，BG=B′G，在直角三角形EFB′中，利用勾股定理求出B′E的长，由AE−B′E求出AB′的长，设AG=x，由AB−AG表示出BG，即为B′G，在直角三角形AB′G中，利用勾股定理列出关于x的方程，求出方程的解得到x的值，确定出AG的长，进而求出BG的长，在直角三角形GBF中，利用勾股定理即可求出折痕FG的长；(ii)当G在AE上，B′落在ED上，如图2所示，同理求出B′E的长，设A′G=AG=y，由AE+B′E−AG表示出GB′，在直角三角形A′B′G中，利用勾股定理列出关于y的方程，求出方程的解得到y的值，求出AG的长，由AE−AG求出GE的长，在直角三角形GEF中，利用勾股定理即可求出折痕FG的长，综上，得到所有满足题意的折痕FG的长．
此题考查了翻折变换−折叠问题，涉及的知识有：矩形的判定与性质，勾股定理，利用了方程、转化及分类讨论的思想，是一道综合性较强的试题．

19.【答案】解：由题意，知两个大菱形的边长为：0.62+0.22=1510(m)．
小菱形的边长为：0.32+0.12=11010(m)．
所以三个菱形的周长的和为：1510×8+11010×4=210(m)．
所以所需铁棍的总长为：1.8×9+2.4×2+210=(21+210)m.
答：需要(21+210)m的铁棍． 
【解析】由勾股定理易求两个大菱形的边长以及小菱形的边长，则三个菱形的周长的和可求出，进而可求出所需铁棍的总长．
本题考查了菱形的性质以及勾股定理的应用，熟记菱形的各种性质是解题的关键．

20.【答案】0.67  33  C 
【解析】解：(1)由表可知，若从盒子里随机摸岀一只球，则摸到白球的概率的估计值为0.67，
故答案为：0.67；

(2)根据题意得：
100×(1−0.67)=33(只)，
答：盒子里黑球有33只；
故答案为：33；

(3)A.从一副扑克牌中任意抽取一张，这张牌是“红色的”的概率为=2754=0.5<0.67，故此选项不符合题意；
B.掷一枚质地均匀的硬币，落地时结果是“正面朝上”的概率为12=0.5，不符合题意；
C.掷一个质地均匀的正六面体骰子(面的点数标记分别为1到6)，落地时面朝上的点数小于5的概率为46≈0.67，符合题意；
所以某小组在“用频率估计概率”的试验中，符合这一结果的试验最有可能的是C，
故答案为：C．
(1)由表中n的最大值所对应的频率即为所求；
(2)根据黑球个数=球的总数×得到的黑球的概率，即可得出答案；
(3)试验结果在0.67附近波动，即其概率P≈0.67，计算三个选项的概率，约为0.67者即为正确答案．
此题考查利用频率估计概率．大量反复试验下频率稳定值即概率．用到的知识点为：部分的具体数目=总体数目×相应频率．

21.【答案】60人  108° 
【解析】解：(1)在抽取的240人中最喜欢A套餐的人数为：240×25%=60(人)，
C套餐人数为240−60−84−24=72(人)，
“C”对应扇形的圆心角的大小为：360°×72240=108°；
故答案为：60人；108°．
(2)960×84240=336(人)，
答：最喜欢B套餐的人数为336人．
(1)根据A套餐的百分比乘以样本容量即可得到人数．用360°乘以C套餐的百分比即可；
(2)用总人数乘以样本中B套餐的百分比即可．
本题主要考查条形统计图和扇形统计图之间的对应关系、熟练掌握各项对应的百分比与总数之间的关系是解题的关键．

22.【答案】解：(1)如图，△A1B1C1为所作；
(2)如图，△A2B2C2为所作．

(3)△A1B1C1绕点P旋转可得到△A2B2C2，则点P点坐标为(−1,0)． 
【解析】(1)利用网格特点和旋转的性质画出A、B、C的对应点A1、B1、C1即可；
(2)根据点A和A2的坐标特征确定平移的方向和距离，利用次平移规律写出点B2、C2的坐标，然后描点即可；、
(3)连接A1A2、C1C2、B1B2，它们都经过点(−1,0)，从而得到旋转中心点P．
本题考查了作图−旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．也考查了平移变换．

23.【答案】解：(1)∠1<∠B；理由如下：
∵四边形ABCD为平行四边形，
∴∠ADC=∠B，
∵D为平行四边形ABCD的钝角顶点，
∴∠1<∠ADC，
∴∠1<∠B；
(2)∵DE、DF为平行四边形的两条高线，
∴S平行四边形ABCD=AB⋅DE=BC⋅DF，
∴ABBC=DFDE=5cm4cm=54，
∴设AB=5xcm，则BC=4xcm，
∵平行四边形ABCD的周长为36cm，
∴2(4x+5x)=36，
解得：x=2，
∴AB=5×2=10(cm)，
∴S平行四边形ABCD=AB⋅DE=10×4=40(cm2)． 
【解析】(1)根据平行四边形的性质进行判断即可；
(2)根据等积法和平行四边形的周长，求出平行四边形的边长，然后再求出平行四边形的面积即可．
本题主要考查了平行四边形的性质，一元一次方程的应用，解题的关键是熟练掌握平行四边形的性质．

24.【答案】解：(1)连接AC，DE交于点N，连接BN并延长，交AD于点M，则点M即为所求作的点，如图所示：

∵四边形ABCD为正方形，
∴∠BAN=∠DAN，AB=AD，
∵AN=AN，
∴△ABN≌△ADN(SAS)，
∴∠ABM=∠ADE，
∵∠BAM=∠DAE，AB=AD，
∴△ABM≌△ADE(ASA)，
∴AM=AE．
(2)连接AC、BD交于点O，连接EO并延长交CD于点F，则点F为所求作的点，如图所示：

连接ED，BF，
∵四边形ABCD为正方形，
∴AB//CD，BO=DO，
∴∠OEB=∠OFD，∠OBE=∠ODF，
∴△OBE≌△ODF(AAS)，
∴BE=DF，
∵BE//DF，
∴四边形BEDF为平行四边形，
∴BF=DE． 
【解析】(1)连接AC，DE交于点N，连接BN并延长，交AD于点M，则点M即为所求作的点；
(2)连接AC、BD交于点O，连接EO并延长交CD于点F，则点F为所求作的点．
本题主要考查了正方形的性质，平行四边形的判定和性质，全等三角形的判定和性质，平行线的性质，解题的关键是熟练掌握三角形全等的判定方法，正方形的性质．

25.【答案】(1)证明：∵EF是AC的垂直平分线，
∴AO=OC，∠AOE=∠COF=90°，
∵四边形ABCD是矩形，
∴AD//BC，
∴∠EAO=∠FCO，
在△AEO和△CFO中，
∠EAO=∠FCOAO=CO∠AOE=∠COF，
∴△AEO≌△CFO(ASA)；
∴OE=OF
又∵OA=OC，
∴四边形AECF是平行四边形，
又∵EF⊥AC
∴平行四边形AECF是菱形；

(2)解：设AF=x，
∵EF是AC的垂直平分线，
∴AF=CF=x，BF=8−x，
在Rt△ABF中，由勾股定理得：AB2+BF2=AF2，
42+(8−x)2=x2，
解得x=5．
∴AF=5，
∴菱形AECF的周长为20． 
【解析】(1)根据ASA推出：△AEO≌△CFO；根据全等得出OE=OF，推出四边形是平行四边形，再根据EF⊥AC即可推出四边形是菱形；
(2)根据线段垂直平分线性质得出AF=CF，设AF=x，推出AF=CF=x，BF=3−x，在Rt△ABF中，由勾股定理得出方程62+(8−x)2=x2，求出即可．
本题考查了勾股定理，矩形性质，平行四边形的判定，菱形的判定，全等三角形的性质和判定，平行线的性质等知识点的综合运用，用了方程思想．

26.【答案】解：(1)BE=AF且BE⊥AF；理由如下：
∵四边形ABCD为正方形，
∴AB=AD，∠BAD=∠ADC=90°，
∵点E、F以相同的速度同时向终点D、C运动，
∴AE=DF，
在△BAE与△ADF中，
AE=DF∠BAE=∠ADFAB=AD，
∴△BAE≌△ADF(SAS)，
∴BE=AF，∠ABE=∠DAF，
∵∠DAF+∠BAH=∠BAD=90°，
∴∠ABH+∠BAH=90°，
∴∠AHB=180°−90°=90°，
∴BE⊥AF；
(2)存在；例如当点E运动到点D，点F运动到点C时，DH+HG=2+22；
∵∠AHB=90°，
∴△ABH为直角三角形，
∵G为AB的中点，
∴GH=12AB=2，
即GH始终等于2，
当点E运动到点D，点F运动到点C时，BE，AF正好为正方形ABCD的对角线，点H正好为对角线的交点，
∵BD=42+42=42，
∴DH=12BD=22，
∴此时DH+HG=2+22．
 
【解析】(1)根据SAS证明△BAE≌△ADF，得出BE=AF，∠ABE=∠DAF，证明∠AHB=180°−90°=90°，即可得出BE⊥AF；
(2)根据直角三角形斜边上中线等于斜边的一半，得出GH始终等于2，当点E运动到点D，点F运动到点C时，BE，AF正好为正方形ABCD的对角线，点H正好为对角线的交点，根据勾股定理求出BD=42+42=42，得出DH=12BD=22，从而得出此时DH+HG=2+22．
本题主要考查了正方形的性质，三角形全等的判定和性质，垂直的定义，直角三角形的性质，勾股定理，解题的关键是熟练掌握正方形的性质，证明△BAE≌△ADF．

27.【答案】(1)证明：∵∠ACB=90°，
∴∠ACE=180°−∠ACB=90°，
∴∠ACB=∠ACE，
在△BCD和△ACE中，
BC=AC∠BCD=∠ACECD=CE，
∴△BCD≌△ACE(SAS)；
(2)解：结论：四边形ABDF是平行四边形，
理由：延长BD交AE于点H，

∵将AE绕A点逆时针旋转90°到AF，
∴AE=AF，∠EAF=90°，
∵△BCD≌△ACE，
∴BD=AE，∠CAE=∠CBD，
∴AF=BD，
∵∠E+∠CAE=90°，
∴∠E+∠CBD=90°，
∴∠AHB=90°=∠FAE，
∴AF//BH，
∴AF//BD，
∵AF=BD，
∴四边形ABDF是平行四边形；
(3)解：连接AG、CG，过点G作GH⊥CE交CE延长线于H，GN⊥AC于N，

∵∠ACB=90°，AC=BC，
∴BC=AC=4，
∵GH⊥CE，GN⊥AC，∠ACH=90°，
∴四边形CHGN是矩形，
∵AF=AE，∠EAF=90°，G是EF中点，
∴AG=GE，AG⊥EF，
∵∠CAG+∠ACH+∠CEG+∠AGE=360°，
∴∠CAG+∠CEG=180°，
∵∠CEG+∠GEH=180°，
∴∠CAG=∠GEH，
又∵∠ANG=∠GHE=90°，
∴△ANG≌△EHG(AAS)，
∴NG=GH，
∴四边形CHGN是正方形，
∴CG平分∠ACH，
∴点G在∠ACH的角平分线上运动，
∴当D从C运动到A点，G点所经过的路径长是以AC为边的正方形的对角线长度的一半，
即为22AC=22×4=22． 
【解析】(1)由题意可得∠BCD=∠ACE，继而利用SAS进行证明即可；
(2)延长BD交AE于点H，由旋转的性质和全等三角形的性质可得BD=AE=AF，∠CAE=∠CBD，∠EAF=90°，由余角的性质可得∠AHB=90°=∠FAE，从而可得AF//BH，由此即可求得结论；
(3)求出点G在∠ACH的解平分线上运动即可求得答案．
本题考查了正方形的判定与性质，全等三角形的判定与性质，等腰直角三角形的判定与性质，旋转的性质等，正确添加辅助线，熟练运用相关知识是解题的关键．

28.【答案】解：(1)∵四边形ABCD是矩形，
∴AD=BC=OC=10，CD=AB=OA=6，∠AOC=∠ECF=90°，
由折叠性质得：EF=DE，AF=AD=10，
∴CE=CD−DE=CD−EF=6−EF，
由勾股定理得：BF=OF=AF2−OA2=102−62=8，
∴FC=OC−OF=10−8=2，
在Rt△ECF中，由勾股定理得：EF2=CE2+FC2，
即：EF2=(6−EF)2+22，
解得：EF=103；
(2)①如图1所示：
当AB为平行四边形的对角线时，AG=BF=8，AG//BF，
∴点G的坐标为：(−8,6)；
当AF为平行四边形的对角线时，AG=BF=8，AG//BF，
∴点G的坐标为：(8,6)；
当BF为平行四边形的对角线时，FG=AB，=6，FG//AB，
∴点G的坐标为：(8,−6)；
综上所述，点G的坐标为(−8,6)或(8,6)或(8,−6)；
②∵四边形AOGF为菱形，
∴OA=AF=10，
∴矩形ABCD平移距离m=OA−AB=10−6=4，
即OB=4，
设FG交x轴于H，如图2所示：
∵OA//FG，BC//x轴，
∴∠FBO=∠BOH=∠OHF=90°，
∴四边形OBFH是矩形，
∴FH=OB=4，OH=BF=8，
∴HG=10−4=6，
∴点G的坐标为：(8,−6)． 
【解析】(1)由矩形的性质得AD=BC=OC=10，CD=AB=OA=6，∠AOC=∠ECF=90°，由折叠性质得EF=DE，AF=AD=10，则CE=6−EF，由勾股定理求出BF=OF=8，则FC=OC−OF=2在Rt△ECF中，由勾股定理得出方程，解方程即可；
(2)①分三种情况，当AB为平行四边形的对角线时；当AF为平行四边形的对角线时；当BF为平行四边形的对角线时，分别去点G的坐标即可；
②由菱形的性质得OA=AF=10，则矩形ABCD平移距离m=OA−AB=4，即OB=4，设FG交x轴于H，证出四边形OBFH是矩形，得FH=OB=4，OH=BF=8，则HG=6，即可得出答案．
本题是四边形综合题目，考查了矩形的判定与性质、坐标与图形性质、平行四边形的性质、勾股定理、折叠变换的性质、平移的性质等知识；本题综合性强，熟练掌握矩形的性质和折叠的性质是解题的关键．