三角函数图像及性质专题讲义-2023二轮复习.docx

这是一份三角函数图像及性质专题讲义-2023二轮复习.docx，共31页。

【课前诊断】
成绩（满分10）： 完成情况： 优/中/差
1．若点在角的终边上，则
A． B．C． D．
2．如图，角以为始边，它的终边与单位圆O相交于点，且点的横坐标为，则的值为
A． B． Ｃ． Ｄ．
3.若角的终边经过点，则的值为
4.若为任意角，则满足的一个值为
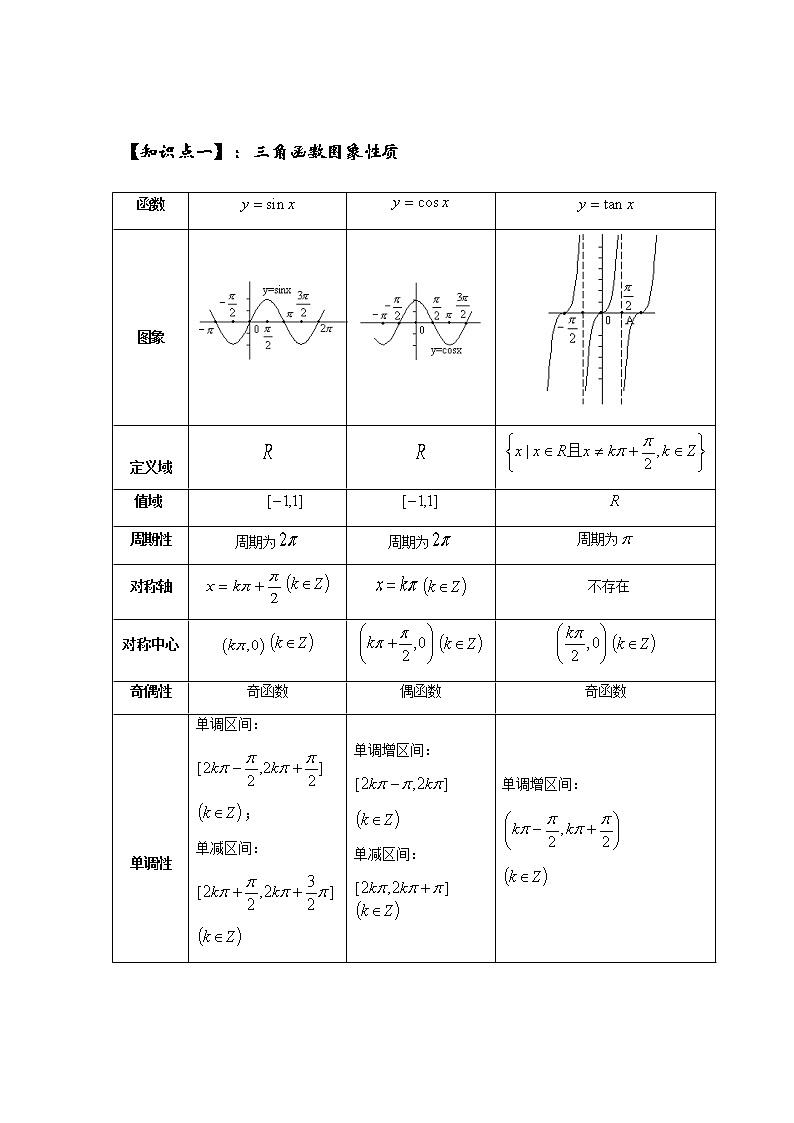
【知识点一】：三角函数图象性质
【典型例题】
考点一： 由三角函数解析式求性质
例1.函数图像的两条相邻对称轴之间的距离是
（A）（B）（C）（D）
例2.函数的最小正周期是__________,最小值是__________.
函数的单调递增区间是.
例4.函数的图像记为曲线,则“”是“曲线关于直线对称”的
（A）充分而不必要条件（B）必要而不充分条件
（C）充分必要条件（D）既不充分也不必要条
例5.设函数,若函数恰有三个零点,,,则的取值范围是
（A）（B）（C）（D）
练习1.已知函数的最小正周期为，则
（A）函数的图象关于原点对称
（B）函数的图象关于直线对称
（C）函数图象上的所有点向右平移个单位长度后，所得图象关于原点对称
（D）函数在区间上单调递增
练习2. “”是“函数的图象关于直线对称”的
（A）充分而不必要条件（B）必要而不充分条件
（C）充分必要条件（D）既不充分也不必要条件
练习3.函数图像的两条相邻对称轴之间的距离是
（A）（B）（C）（D）
考点二：由三角函数图象及性质求解析式
例1.函数,的部分图象如图所示,则的值分别是
O
2
-2
（A）
（B）
（C）
（D）
例2.已知函数,若函数的部分
图象如图所示,则,的最小值是.
例3.若函数(,)的部分图象如图所示,则,.
例4．已知函数（其中,）的部分图象如图所示,则,．
例5.已知函数,若,则函数的单调增区间为________.
例6.已知函数，点，都在曲线上，且线段与曲线有五个公共点，则的值是
（A）4（B）2（C）（D）
例7.已知函数在一个周期内的图象如图所示,其中分别是这段图象的最高点和最低点,是图象与轴的交点,且,则的值为
（A）
（B）
（C）
（D）
例8.设函数是常数,).若在区间上具有单调性,且,则的最小正周期为.

练习1.函数(,,)的部分图象如图所示,则函数表达式为
（A）
（B）
（C）
（D）
练习2.设函数.若对任意的实数都成立,则的最小值为.
练习3.已知点A,B,C,若这三个点中有且仅有两个点在函数的图像上,则正数的最小值为.
考点三：三角恒等变换与图象性质综合
例1.已知函数．
（Ⅰ）求的最小正周期;
（Ⅱ）求在上的最大值．

例2.已知函数的最小正周期为.
（Ⅰ）求的值;
（Ⅱ）求的单调递增区间.
例3.已知函数.
（Ⅰ）求的定义域及的值;
（Ⅱ）求在上的单调递增区间.
例4.已知函数,.
（Ⅰ）若,求的单调递增区间;
（Ⅱ）若,求的最小正周期的表达式并指出的最大值.
例5.已知函数
（Ⅰ）求的最小正周期;
（Ⅱ）若在区间上的最大值为,求的最小值.
例6.已知函数,.
（Ⅰ）求的最小正周期和单调递增区间;
（Ⅱ）设,若函数为奇函数,求的最小值.
例7.函数的部分图象如图所示.
（Ⅰ）写出的最小正周期及图中,的值;
（Ⅱ）求在区间上的最大值和最小值.
例8.如图,已知函数在一个周期内的图象经过 三点.
（Ⅰ）写出的值;
（Ⅱ）若且 求的值.
练习1. 已知.
（Ⅰ）的最小正周期及单调增区间;
（Ⅱ）若时,求的值域.
练习2.已知函数.
（Ⅰ）求的最小正周期;
（Ⅱ）当时,求函数的单调递减区间.
练习3.函数的部分图象如图所示．
（Ⅰ）求的值;
（Ⅱ）求的值．
考点四：三角函数应用题
例1.如图,一个半径为米的水轮按逆时针方向每分钟转圈,记水轮上的点到水面的距离为米（在水面
下则为负数）,如果（米）与时间（秒）之间满足关系,
且当点从上面上浮现时开始计算时间,那么以下结论中:
②③④
正确结论的序号是.
例2.去年某地的月平均气温与月份（月）近似地满足函数（为常数）.若月份的月平均气温约为℃,月份的月平均气温约为℃,则该地月份的月平均
气温约为℃.
练习1.如图，弹簧挂着一个小球作上下运动，小球在秒时相对于平衡位置的高度（厘米）由如下关系式确定：，则小球在开始振动（即）时的值为_________，小球振动过程中最大的高度差为__________厘米.
考点五：三角函数与其他函数结合
例1.已知函数是偶函数,则下列结论可能成立的是 （ ）
（A）（B）
（C）（D）
例2.已知函数 ,下列结论中错误的是（ ）
（A）是偶函数 （B）函数最小值为
（C） 是函数的一个周期（D）函数在内是减函数
例3.“”是“函数在上单调递增”的 （ ）
（A）充分不必要条件（B）必要不充分条件
（C）充分必要条件（D）既不充分也不必要条件
练习1.设函数,则的最小正周期 （ ）
（A）与有关,且与有关（B）与有关,但与无关
（C）与无关,且与无关（D）与无关,但与有关
练习2.设（）,则下列说法不正确的是 （ ）
（A）为上偶函数 （B）为的一个周期
（C）为的一个极小值点（D）在区间上单调递减
【知识点二】：三角函数图象变换（函数图像变换的本质是点的变换）
一.函数图象平移基本结论小结如下：
设为左移个单位后所得图象上的任意一点，则将Ｐ右移个单位得到的必在的图象上，故，又点任意，故的图象左移个单位得到的新的函数的解析式为：．
函数变换可以用下图表示：

考点一： 三角函数伸缩平移变换
例1.将的图象向左平移个单位,则所得图象的函数解析式为
（A）（B）
（C）（D）
例2.要得到函数的图象,只需将函数的图象上所有的点
（A）先向右平移个单位长度,再将横坐标伸长为原来的倍,纵坐标不变
（B）先向右平移个单位长度,横坐标缩短为原来的倍,纵坐标不变
（C）横坐标缩短为原来的倍,纵坐标不变,再向右平移个单位长度
（D）横坐标变伸长原来的倍,纵坐标不变,再向右平移个单位长度
例3.将函数的图象向左平移个单位后与函数的图象重合,则函数为
（A）（B）
（C）（D）
例4.已知函数.若的图像向左平移个单位所得的图像与的图像重合,则的最小值为.
例5.将函数的图象向左平移个单位长度,得到函数图象在区间上单调递减,则的最小值为
（A）（B）（C）（D）
练习1.已知函数的最小正周期为,则
（A）函数的图象关于原点对称
（B）函数的图象关于直线对称
（C）函数图象上的所有点向右平移个单位长度后,所得的图象关于原点对称
（D）函数在区间上单调递增
练习2.已知函数.若的图像向左平移个单位所得的图像与的图像重合,则的最小值为.
练习3. 已知函数的最小正周期为,为了得到函数的图象,只要将的图象
（A）向左平移个单位长度（B）向右平移个单位长度
（C）向左平移个单位长度（D）向右平移个单位长度
【小试牛刀】
1.若函数(,)的部分图象如图所示,则.

2.设,若函数的最小正周期为,则______
3.函数的一条对称轴方程为
（A）（B）（C）（D）

4.函数的图像记为曲线,则“”是“曲线关于直线对称”的
（A）充分而不必要条件（B）必要而不充分条件
（C）充分必要条件（D）既不充分也不必要条件
5.已知函数是偶函数,则下列结论可能成立的是
（A）（B）
（C）（D）
6.设函数，，则“”是“函数为奇函数”的
（A）充分而不必要条件（B）必要而不充分条件
（C）充分必要条件（D）既不充分也不必要条件
7.函数是
（A）最小正周期为的偶函数（B）最小正周期为的奇函数
（C）最小正周期为的偶函数（D）最小正周期为的奇函数
8.已知函数(其中)的部分图象,如图所示.那么的解析式为
（A）
（B）
（C）
（D）
9.函数y=Asinωx+φ（ω>0,φ<π2,x∈R）的部分图像如图所示，则函数表达式为
（A）y=-4sin(π8x-π4)（B）y=-4sin(π8x+π4)
（C）y=4sin(π8x-π4)（D）y=4sin(π8x+π4)
10.设函数的图象为,下面结论中正确的是
（A）函数的最小正周期是
（B）图象关于点对称
（C）图象可由函数的图象向右平移个单位得到
（D）函数在区间上是增函数
11.关于函数有下列三个结论:
= 1 \* GB3 ①函数的最小正周期为
= 2 \* GB3 ②函数的最大值为
= 3 \* GB3 ③函数在区间单调递减
其中,正确结论的序号是
（A） = 1 \* GB3 ① = 2 \* GB3 ②（B） = 1 \* GB3 ① = 3 \* GB3 ③（C） = 2 \* GB3 ② = 3 \* GB3 ③（D） = 1 \* GB3 ① = 2 \* GB3 ② = 3 \* GB3 ③
12.已知函数,是的导函数,则下列结论中正确的是
（A）函数的值域与的值域不同
（B）存在,使得函数和都在处取得最值
（C）把函数的图象向左平移个单位,就可以得到函数的图象
（D）函数和在区间上都是增函数
13.已知函数,下列结论中错误的是
（A）的图像关于中心对称
（B）的图像关于直线对称
（C）的最大值为
（D）既奇函数，又是周期函数
14.将函数的图象向右平移个单位后,图象经过点,则的最小值为
（A）（B）（C）（D）
15.已知函数在一个周期内的部分对应值如下表:
（Ⅰ）求的解析式;
（Ⅱ）求函数的最大值和最小值.
16.已知函数.
（Ⅰ）求函数的最小正周期;
（Ⅱ）求函数在区间上的最大值与最小值的和.
【巩固练习——基础篇】
1.函数的图象
A．关于对称B．关于y轴对称
C．关于原点对称D．关于对称
2.函数的最大值是3，则它的最小值_____________________.
3.函数的部分图象是
A.B.C.D.
4.函数的部分图象如图所示,则
5.将函数的图象上所有的点向右平行移动个单位长度,再把所得各点的横坐标缩短到原来的（纵坐标不变）,所得图象的函数解析式是
（A）（B）
（C）（D）
6.如果函数的图象过点且,那么____;____.
7.已知函数.
（Ⅰ）求的最小正周期和在上的单调递减区间;
（Ⅱ）若为第四象限角,且,求的值.
【巩固练习——提高篇】
1．若函数在区间上有且只有一个零点,则实数.
2.将函数的图象向左平移个单位长度后,所得到的图像关于原点对称,则的最小值是.
3.如果函数的两个相邻零点间的距离为,那么的值为 （ ）
（A）1(B)-1(C) （D）
4.已知函数,在曲线与直线的交点中,若相邻交点距离的最小值为,则的最小正周期为.
5.已知函数,若关于的方程在内有唯一实根,则实数的最小值是
6.已知函数,.
（Ⅰ）求函数的最小正周期;
（Ⅱ）若,求函数的单调增区间.
7.已知函数.
（Ⅰ）求的最小正周期和对称轴方程;
（Ⅱ）求在区间上的最小值.
8.已知函数.
(Ⅰ)若，求的值；
(Ⅱ)若在上单调递减，求的最大值.
9.已知函数.
（Ⅰ）求的定义域及最小正周期;
（Ⅱ）求的单调递减区间.
10.已知函数.
（Ⅰ）求的定义域;
（Ⅱ）求的取值范围.
11.函数(,)的部分图像如图所示,其中是函数的一个零点.
（Ⅰ）写出,及的值;
（Ⅱ）求函数在区间上的最大值和最小值.
12.已知函数.
（Ⅰ）求曲线的相邻两条对称轴的距离;
（Ⅱ）若函数在区间上单调递增,求的最大值.
A．
B．
C．
D．
A．
B．
C．
D．
函数
图象
定义域
值域


周期性
周期为
周期为
周期为
对称轴
不存在
对称中心
奇偶性
奇函数
偶函数
奇函数
单调性
单调区间：
；
单减区间：
单调增区间：
单减区间：
单调增区间：