2022-2023学年湖南省衡阳市衡南县高二上学期期末数学试题（解析版）

2022-2023学年湖南省衡阳市衡南县高二上学期期末数学试题

一、单选题

1．设复数满足，是虚数单位，则

A． B． C． D．

【答案】A

【详解】，故选A.

2．已知集合，则集合的所有非空真子集的个数是（    ）

A．6 B．7 C．14 D．15

【答案】A

【分析】根据自然数集的特征，结合子集的个数公式进行求解即可.

【详解】因为，

所以集合的元素个数为，

因此集合的所有非空真子集的个数是，

故选：A

3．点关于轴的对称点的坐标为（    ）

A． B． C． D．

【答案】C

【分析】根据关于坐标轴对称的点的坐标特征可直接求得结果.

【详解】两个关于轴对称的点的坐标特征为：坐标相同，坐标互为相反数，

点关于轴对称的点的坐标为.

故选：C.

4．数列中，，，若，则（    ）

A．10 B．9 C．11 D．8

【答案】B

【分析】根据递推关系求得，由此列方程求得.

【详解】，

令，则，

所以是首项为，公比为的等比数列，

所以，

由得.

故选：B

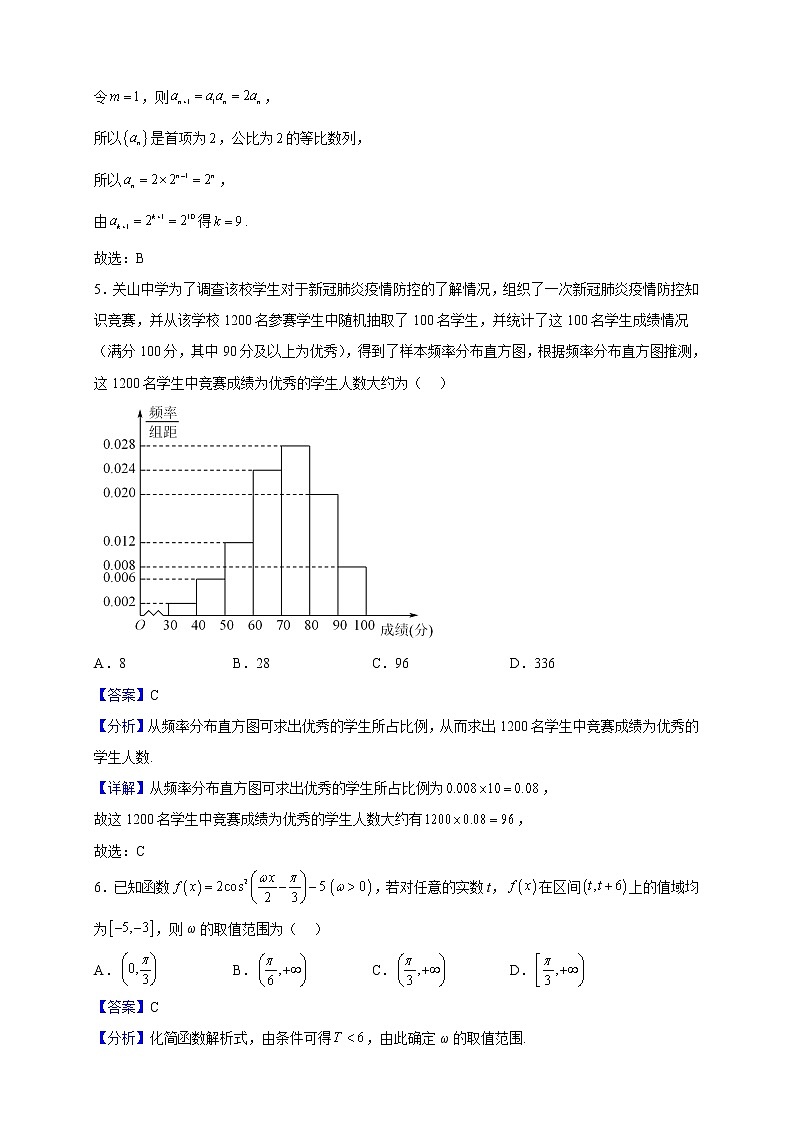
5．关山中学为了调查该校学生对于新冠肺炎疫情防控的了解情况，组织了一次新冠肺炎疫情防控知识竞赛，并从该学校1200名参赛学生中随机抽取了100名学生，并统计了这100名学生成绩情况（满分100分，其中90分及以上为优秀），得到了样本频率分布直方图，根据频率分布直方图推测，这1200名学生中竞赛成绩为优秀的学生人数大约为（    ）

A．8 B．28 C．96 D．336

【答案】C

【分析】从频率分布直方图可求出优秀的学生所占比例，从而求出1200名学生中竞赛成绩为优秀的学生人数.

【详解】从频率分布直方图可求出优秀的学生所占比例为，

故这1200名学生中竞赛成绩为优秀的学生人数大约有，

故选：C

6．已知函数，若对任意的实数t，在区间上的值域均为，则ω的取值范围为（    ）

A． B． C． D．

【答案】C

【分析】化简函数解析式，由条件可得，由此确定ω的取值范围.

【详解】，又

则的最小正周期，函数在上的最大值为-3，最小值为-5，

因为对任意的实数t，在区间上的值域均为，

所以在区间上既能取得最大值-3，也能取得最小值-5，

所以，解得．

所以ω的取值范围为，

故选：C．

7．如图是来自古希腊数学家希波克拉底所研究的几何图形，此图由三个半圆构成，三个半圆的直径分别为直角的斜边，直角边，．若，，E为半圆弧的中点，F为半圆弧上的任一点，则的最大值为（    ）

A． B． C． D．4

【答案】B

【分析】如图，以为轴建立平面直角坐标系，则，，求出点坐标，写出半圆弧的方程，设出点坐标，用坐标法计算，利用三角函数性质求得最大值．

【详解】如图，以为轴建立平面直角坐标系，则，，

，，，

半圆弧的方程为，

设（），

，

，

，则，时取得最小值是，

所以取得最大值．

故选：B.

8．《九章算术·商功》：“斜解立方，得两堑堵，其一为阳马，一为鳖臑，阳马居二，鳖臑居一.”下图解释了这段话中由一个长方体得到堑堵、阳马、鳖臑的过程.在一个长方体截得的堑堵和鳖臑中，若堑堵的内切球（与各面均相切）半径为1，则鳖臑体积的最小值为（    ）

A． B． C． D．

【答案】C

【分析】根据堑堵的内切球半径列方程，求得鳖臑体积的表达式，结合基本不等式求得鳖臑体积的最小值.

【详解】依题意，堑堵的内切球（与各面均相切）半径为，

所以直角三角形的内切圆半径为，，

设，则，

所以，

，

当且仅当时等号成立，

则，

所以鳖臑体积.

故选：C

二、多选题

9．下列说法正确的是（    ）

A．若不等式的解集为，则

B．若命题p：，，则p的否定为，

C．已知函数在上是增函数，则实数a的取值范围是

D．已知.若的值域为R，则实数m的取值范围

【答案】AB

【分析】对于A，不等式解集的端点即对应方程的根，可求出，判断正误；

对于B，使用含有一个量词的命题的否定的知识进行判断；

对于C，结合函数单调性的定义，结合分段函数单调性知识进行判断；

对于D，可使用复合函数的值域知识进行判断.

【详解】对于A，不等式的解集为，

则和是方程的两个根，故，

解得，所以，故A正确；

对于B，全称量词命题“，”的否定为存在量词命题“，”

因此命题，则其否定为，故B正确；

对于C，因为是增函数，需满足当时，为增函数，当时，为增函数，且当时，，所以，解得，故C不正确；

对于D，令，，的值域为R，则的值域为R，即为值域的子集，当时，，值域为R，满足题意，当时，需，即，解得，综上所述，实数的取值范围是，故D不正确.

故选：AB.

10．已知圆C：及点，则下列说法正确的是（    ）

A．直线与圆C始终有两个交点

B．圆C与轴不相切

C．若点在圆C上，则直线PQ的斜率为

D．若M是圆C上任一点，则|MQ|的取值范围为

【答案】BD

【分析】求出圆C的圆心坐标和半径，求出直线过的定点判断A；求出点C到x轴距离判断B；求出m值，再计算斜率判断C；求出长并求出范围判断D作答.

【详解】依题意，圆C：，圆心，半径，

对于A，直线恒过定点，而点在圆C外，则过点的直线与圆C可能相离，A不正确；

对于B，点到x轴距离为7，大于圆C的半径，则圆C与轴相离，即圆C与x轴不相切，B正确；

对于C，点在圆C上，则，解得，而点，

则直线PQ的斜率为，C不正确；

对于D，，点Q在圆C外，由得：，D正确.

故选：BD

11．已知a，b，c为三条不同的直线，，，为三个不同的平面，则下列说法错误的是（    ）

A．若，，则

B．若，，，，则

C．若，，，，则

D．若，，，则

【答案】ACD

【分析】由线面平行的判定定理与性质定理，线面垂直的判定定理，面面平行的判定定理判断各选项．

【详解】选项A中，需要加条件才能得线面平行，A错；

选项B，，，，则，，，则，所以，B正确；

选项C，需要加条件相交，才能得出线面垂直，C错；

选项D，三棱柱的三条侧棱两两平行，但它们所在的平面是相交的不平行，D错．

故选：ACD．

12．已知抛物线：的焦点为，准线为，经过点的直线与抛物线相交，两点，，在上的射影分别为，，与轴相交于点，则下列说法正确的是（    ）

A． B．

C．若，则 D．若，，则

【答案】ACD

【分析】设，联立直线和抛物线方程得到韦达定理，得到，即得选项A正确；，所以选项B错误；求出即得选项C正确；由题得,求出，即得选项D正确.

【详解】解：设，则，

当直线斜率显然不能为零，设其方程为，联立抛物线方程得，所以 .

所以，所以，所以选项A正确；

所以，所以选项B错误；

如图，设 过点作 ，则，

由题得直线的斜率为,

所以，

所以，所以选项C正确；

由题得,

所以 ，

所以.

所以.

所以选项D正确.

故选：ACD

三、填空题

13．一组数据21，30，53，41，35，76，37，18，29，10，第80百分位数是________．

【答案】47

【分析】根据百分位的定义可得第80百分位数是第8个和第9个数据的平均数，计算即可得解.

【详解】把21，30，53，41，35，76，37，18，29，10，进行从小到大排序可得：

10，18，21，29，30，35，37，41，53，76，

共10个数据，，

故第80百分位数是第8个和第9个数据的平均数，

即，

故答案为：

14．若数列第二项起，每一项与前一项的差构成等差数列，则称数列为二阶等差数列，已知数列是一个二阶等差数列，且，，，则_______________．

【答案】

【分析】利用已知条件求出二阶等差数列的首项和公差，再求出二阶等差数列的通项公式，最后利用累加法即可得到数列的通项公式.

【详解】，，且数列是一个二阶等差数列，

由累加法得

．而a1=3也符合，

故答案为：

15．如图，在三棱锥中，已知，，，，平面平面，三棱锥的体积为，若点，，，都在球的球面上，则球的表面积为____________．

【答案】

【分析】根据条件分析出球心并求出球的半径，进而即得．

【详解】因为在三棱锥中，，，，，

所以和均为直角三角形，且斜边均为，

所以为球的直径， 的中点为球心，

设，则，，，，且的边高为，

因为平面平面，

根据面面垂直的性质定理可知的边上的高即为三棱锥的高，

因为三棱锥的体积为

，

所以球半径，

所以球的表面积为．

故答案为：．

16．如图，已知梯形中，，点在线段上且，双曲线过三点，且以为焦点．当时，双曲线离心率的取值范围是_________．

【答案】

【分析】建立平面直角坐标系，写出对应点的坐标，根据点满足双曲线方程，建立双曲线离心率与参数之间的函数关系，进而求其值域即可.

【详解】以所在直线为轴、线段的中点为原点建立平面直角坐标系，如下所示：

设过点三点的双曲线方程为：，

根据题意可得：，设两点坐标分别为，

则，

由可得：，解得，

因为点的坐标都满足双曲线方程，故可得：

，则，将其代入，

整理化简可得：，即，

整理得：，又因为，

故可得，则.

故答案为：.

【点睛】关键点睛：本题考查双曲线离心率的求解，解决问题的关键是根据题意，建立离心率与参数之间的关系，同时要注意计算的准确度，属中档题.

四、解答题

17．已知为坐标原点， 倾斜角为的直线与轴的正半轴分别相交于点的面积为.

(1)求直线的方程;

(2)直线， 点在上， 求的最小值.

【答案】(1)

(2)

【分析】(1)根据斜率假设出直线方程，再求出坐标即可求解；(2)求出关于直线对称的点坐标为，将问题转化为求的最小值即可.

【详解】（1）因为,所以设直线的方程为，且，

所以，

所以，解得或（舍）.

所以直线的方程为

（2）由(1)得，

设关于直线对称的点坐标为，

则有 ，解得，所以，

所以.

所以的最小值为.

18．在中，角A，B，C所对的边分别是a，b，c．已知．

(1)求A；

(2)若，且，求的取值范围．

【答案】(1)

(2)

【分析】（1）由正弦定理得，结合，求出；

（2）由正弦定理得到，从而得到，结合，求出，得到的取值范围.

【详解】（1）由，得：

由正弦定理得：

又，所以，

故，即，则；

（2）由正弦定理得：

所以

又因为，所以，又，故，

故，则，所以

故的取值范围为．

19．如图，长方体中，、与底面所成的角分别为60°和45°，且，点P为线段上一点．

(1)求长方体的体积；

(2)求最小值．

【答案】(1)

(2)

【分析】（1）根据长方体边长和体对角线的关系，求出边长得到体积.

（2）利用向量法找到最小值时的位置，求得最小值.

【详解】（1）因为平面，且、与底面所成的角分别为60°和45°，

所以，，因此设，

又，所以，因此，

因为，所以，解得，

故长方体的体积为；

（2）由题意，，

当时，取得最小值，最小值为，

因此的最小值为，故的最小值为．

20．已知数列各项均为正数，且，.

(1)求的通项公式；

(2)设，求是数列的前项和，求.

【答案】(1)

(2)

【分析】（1）化简已知等式可求得，知数列为等差数列，由等差数列通项公式可求得结果；

（2）由（1）可得，分别在为偶数和为奇数的情况下，采用并项求和方法和求得，综合两种情况可得结果.

【详解】（1）由得：，

又，，

，数列是以为首项，为公差的等差数列，

.

（2）由（1）得：；

当为偶数时，；

当为奇数时，；

综上所述：.

21．在四棱锥中，面面ABCD，，，，，，，M是棱PA上一点且．

(1)求证： 平面PCD；

(2)求直线BM与平面PBC所成角的正弦值．

【答案】(1)见详解

(2)

【分析】（1）取AD中点为O点，连结PO、CO，易证PO、CO、OA两两垂直.建立空间直角坐标系，利用空间坐标求得平面的法向量，由，可得，进而证得；

（2）求得平面的法向量，由即可得解.

【详解】（1）取AD中点为O点，连结PO、CO，则.

由已知，，，则有，.

又，在平面ABCD中，有，

由已知可得，为直角三角形，则.

又面面ABCD，面面ABCD=AD，

则面ABCD ，面ABCD ，.

所以，PO、CO、OA两两垂直.

如图建立空间直角坐标系，由题意得，

，，，，.

，，，，故.

设平面的法向量为，则

，即

令，则.

∴.

∴，

∴，又平面，

∴平面.

（2）由（1），， .

则，

设平面的法向量为，则

，即，

令，则.

所以.由（1）知.

所以直线BM与平面PBC所成角的正弦值.

22．已知双曲线的右焦点为，渐近线与抛物线交于点.

(1)求的方程；

(2)设是与在第一象限的公共点，作直线与的两支分别交于点，便得.

（i）求证：直线过定点；

（ii）过作于.是否存在定点，使得为定值？如果有，请求出点的坐标；如果没有，请说明理由.

【答案】(1)，；

(2)（i）答案见解析；（ii）答案见解析.

【分析】（1）利用待定系数法求出的方程；

（2）（i）设方程为.令,利用“设而不求法”得到.表示出,整理可得： .可以判断出直线MN的方程为,即可证明过定点.（ⅱ）由为直角，判断出D在以AB为直径的圆上，得到为AB的中点,使得为定值.

【详解】（1）因为，渐近线经过点，

所以，解得：，所以

抛物线经过点

所以，所以

（2）（i）因为在不同支,所以直线的斜率存在,设方程为.

令,联立得， ，则.

联立可得，解得：.

因为,所以，

代入直线方程及韦达结构整理可得：，

整理化简得：.

因为不在直线MN上,所以.

直线MN的方程为,过定点.

（ⅱ）因为为定点,且为直角，

所以D在以AB为直径的圆上,AB的中点即为圆心,半径为定值.

故存在点,使得为定值.