【备考2023徐州中考】备战2023年江苏徐州中考数学仿真卷（五）

备战2023年江苏徐州中考数学仿真卷（五）

一．选择题（共8小题，满分24分，每小题3分）

1．（3分）的相反数是　　

A．2 B． C． D．

【答案】

【详解】解：的相反数是：，

故选：．

2．（3分）下列图形中，是轴对称图形，但不是中心对称图形的是　　

A． B． 

C． D．

【答案】

【详解】解：、是轴对称图形，但不是中心对称图形；

、既是轴对称图形，又是中心对称图形；

、不是轴对称图形，是中心对称图形；

、既是轴对称图形，又是中心对称图形．

故选：．

3．（3分）下列运算中，结果正确的是　　

A． B． C． D．

【答案】

【详解】解：、由于同底数的幂相除底数不变指数相减，故当时，，故本选项错误；

、，故本选项错误；

、依据幂的乘方运算法则可以得出，故本选项错误；

、，正确．

故选：．

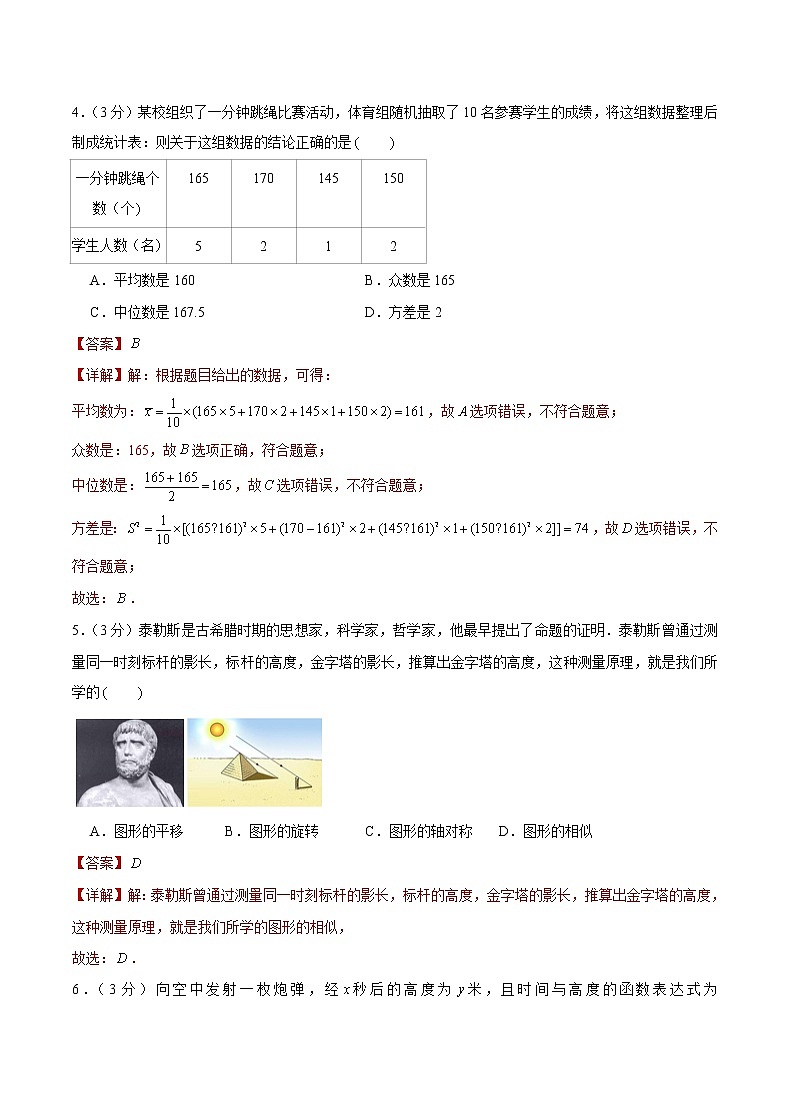
4．（3分）某校组织了一分钟跳绳比赛活动，体育组随机抽取了10名参赛学生的成绩，将这组数据整理后制成统计表：则关于这组数据的结论正确的是　　

A．平均数是160 B．众数是165 

C．中位数是167.5 D．方差是2

【答案】

【详解】解：根据题目给出的数据，可得：

平均数为：，故选项错误，不符合题意；

众数是：165，故选项正确，符合题意；

中位数是：，故选项错误，不符合题意；

方差是：，故选项错误，不符合题意；

故选：．

5．（3分）泰勒斯是古希腊时期的思想家，科学家，哲学家，他最早提出了命题的证明．泰勒斯曾通过测量同一时刻标杆的影长，标杆的高度，金字塔的影长，推算出金字塔的高度，这种测量原理，就是我们所学的　　

A．图形的平移 B．图形的旋转 C．图形的轴对称 D．图形的相似

【答案】

【详解】解：泰勒斯曾通过测量同一时刻标杆的影长，标杆的高度，金字塔的影长，推算出金字塔的高度，这种测量原理，就是我们所学的图形的相似，

故选：．

6．（3分）向空中发射一枚炮弹，经秒后的高度为米，且时间与高度的函数表达式为，若此炮弹在第6秒与第13秒时的高度相等，则下列时间中炮弹所在高度最高的是　　

A．第7秒 B．第9秒 C．第11秒 D．第13秒

【答案】

【详解】解：此炮弹在第6与第13秒时的高度相等，

抛物线的对称轴是：，

炮弹所在高度最高是9.5秒，

在四个选项中炮弹所在高度最高的是9秒．

故选：．

7．（3分）如图，在中，，．分别以点、为圆心，大于的长为半径画弧，两弧交于，两点，直线交于点，连接．以点为圆心，为半径画弧，交延长线于点，连接．若，则的周长为　　

A．8 B．6 C．4 D．

【答案】

【详解】解：由题意可得是线段的垂直平分线，，

则，

，

，

，

的周长为．

故选：．

8．（3分）如图，点，的坐标分别为、，点为坐标平面内的一点，且，点为线段的中点，连接，则的最大值为　　

A． B． C． D．

【答案】

【详解】解：如图，作点关于点的对称点，

则点是的中点，

又点是的中点，

是△的中位线，

，

当最大时，最大，

点为坐标平面内的一点，且，

点在以为圆心，2为半径的上运动，

当经过圆心时，最大，即点在图中位置．

．

的最大值．

故选：．

二．填空题（共10小题，满分30分，每小题3分）

9．（3分）方程组的解是 　　．

【答案】

【详解】解：，

①②得：，

解得：，

把代入②得：，

则方程组的解为，

故答案为：

10．（3分）分解因式：　　．

【答案】

【详解】解：原式．

故答案为：．

11．（3分）若与都是正比例函数图象上的点，则的值是 　　．

【答案】

【详解】解：正比例函数的图象经过点，

，解得，

，

将代入得：，

故答案为：．

12．（3分）用半径为，圆心角为的扇形纸片围成一个圆锥的侧面，则这个圆锥的底面圆半径为　

    ．

【答案】

【详解】解：设圆锥的底面圆半径为，依题意，得

，

解得．

故选：．

13．（3分）写出一个二次函数，其图象满足：①开口向下；②与轴交于点，这个二次函数的解析式可以是　　．

【答案】

【详解】解：设二次函数的解析式为．

抛物线开口向下，

．

抛物线与轴的交点坐标为，

．

取，时，二次函数的解析式为．

故答案为：（答案不唯一）．

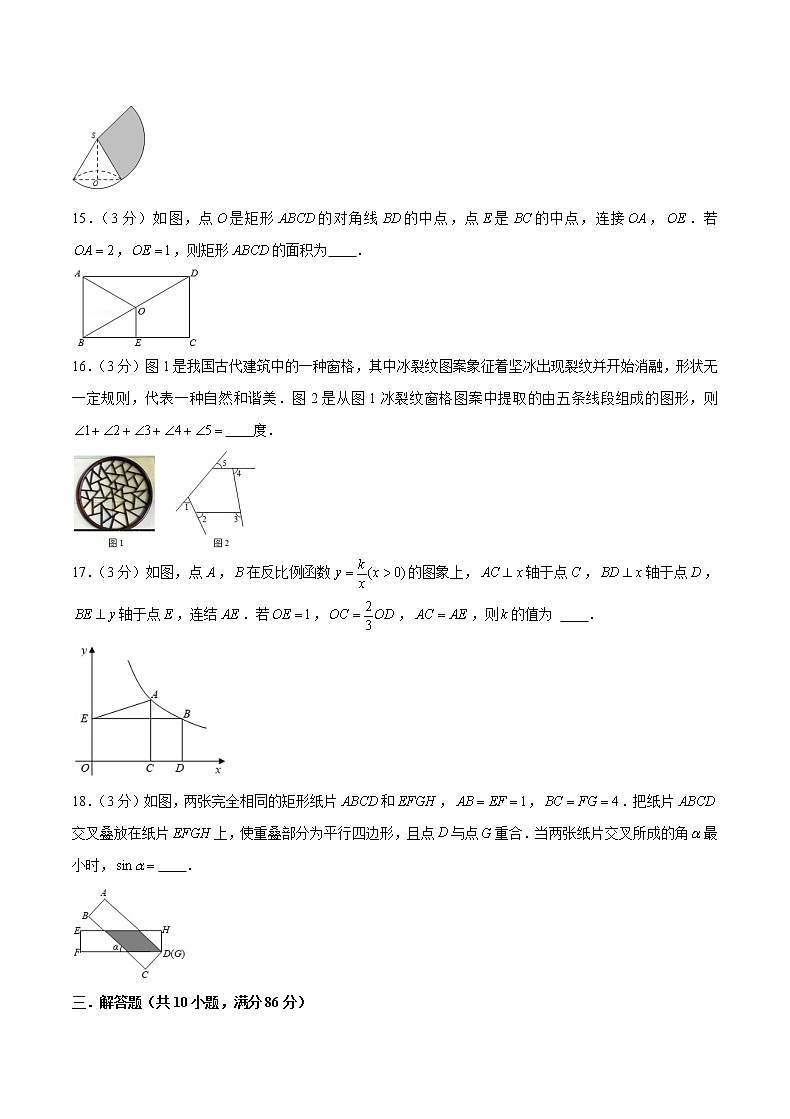
14．（3分）如图，圆锥的底面半径为，高等于，则侧面展开图扇形的圆心角为　　．

【答案】120

【详解】解：设圆锥的侧面展开图扇形的圆心角度数为，

圆锥的底面半径为1，高为，

圆锥的母线长为：，

则，

解得，，

故答案为：120

15．（3分）如图，点是矩形的对角线的中点，点是的中点，连接，．若，，则矩形的面积为　　．

【答案】

【详解】解：为的中点，是的中点，

，

，

，

四边形是矩形，

，，

，

，

，

矩形的面积．

故答案为：．

16．（3分）图1是我国古代建筑中的一种窗格，其中冰裂纹图案象征着坚冰出现裂纹并开始消融，形状无一定规则，代表一种自然和谐美．图2是从图1冰裂纹窗格图案中提取的由五条线段组成的图形，则　　度．

【答案】360

【详解】解：由多边形的外角和等于360度，

可得度．

故答案为：360．

17．（3分）如图，点，在反比例函数的图象上，轴于点，轴于点，轴于点，连结．若，，，则的值为 　　．

【答案】

【详解】解：轴于点，轴于点，

四边形是矩形，

，

把代入，求得，

，

，

，

，

轴于点，

把代入得，，

，

，，

在中，，

，解得，

在第一象限，

，

故答案为：．

18．（3分）如图，两张完全相同的矩形纸片和，，．把纸片交叉叠放在纸片上，使重叠部分为平行四边形，且点与点重合．当两张纸片交叉所成的角最小时，　　．

【答案】

【详解】解：如图，

四边形和四边形是矩形，

，，

，且，，

，

，且四边形是平行四边形，

四边形是菱形，

，

，

当点与点重合时，两张纸片交叉所成的角最小，

设，则，

，

，

，

，

故答案为：．

三．解答题（共10小题，满分86分）

19．（10分）计算：（1）；

（2）．

【答案】（1）；（2）1

【详解】解：（1）

；

（2）

．

20．（10分）（1）解方程：；

（2）解不等式组：．

【答案】（1）；（2）

【详解】解：（1）去分母得：，

解得：，

检验：把代入得：，

分式方程的解为；

（2）由①得：，

由②得：，

不等式组的解集为．

21．（7分）甲、乙两家书店规模相当，去年下半年的月盈利折线统计图如图所示．

（1）①要评价这两家书店月的月盈利的平均水平，应选择计算统计量 　　．

．中位数  ．平均数  ．众数  ．方差

②请分别求出反应这两家书店月盈利“平均水平”的统计量；

（2）根据（1）中所求的统计量，结合折线统计图，你认为去年下半年哪家书店经营状况较好？请简述理由．

【答案】（1）①；②2；（2）甲书店经营状况较好

【详解】解：（1）①要评价这两家书店月的月盈利的平均水平，应选择计算统计量平均数，

故答案为：；

②（万元），

（万元）；

（2）甲书店经营状况较好，

甲书店营业额的平均值大于乙书店，且由折线统计图可知甲书店的营业额持续稳定增长，潜力大．

22．（7分）随着“新冠肺炎”疫情防控形势日渐好转，各地开始复工复学，某校为加强学生自我防护意识，成立“防疫志愿者服务队”，设立三个“监督岗”：①教学楼监督岗，②阅览室监督岗，③就餐监督岗，小宇和小宁两位同学报名参加了志愿者服务工作，在不了解具体岗位的情况下，他们从序号①、②、③中随机填报了一个服务监督岗序号．

（1）小宇填报“③”的概率为 　　；

（2）用列表法或画树状图法，求小宇和小宁同时选到“③就餐监督岗”的概率．

【答案】（1）；（2）

【详解】解：（1）小宇填报“③”的概率为；

故答案为：；

（2）画树状图为：

共有9种等可能的结果，其中小宇和小宁同时选到“③就餐监督岗”的结果数有1种，

小宇和小宁同时选到“③就餐监督岗”的概率为．

23．（8分）我国今年成功举办了北京冬奥会和冬残奥会，吉祥物“冰墩墩”和“雪容融”深受广大民众的喜爱，小王想购买两种吉祥物毛绒玩具，已知购买1件“冰墩墩”和1件“雪容融”共需230元，购买2件“冰墩墩”和3件“雪容融”共需540元，求吉祥物玩具“冰墩墩”和“雪容融”单价分别是多少？

【答案】吉祥物玩具“冰墩墩”的单价是150元，“雪容融”的单价是80元

【详解】解：设吉祥物玩具“冰墩墩”的单价是元，“雪容融”的单价是元，

依题意得：，

解得：．

答：吉祥物玩具“冰墩墩”的单价是150元，“雪容融”的单价是80元．

24．（8分）如图，在坐标平面内，三个顶点的坐标分别为，，（正方形网格中，每个小正方形的边长为，以点为位似中心，把按相似比放大，得到对应的△．

（1）请在第一象限内画出△；

（2）若以点、、、为顶点的四边形是平行四边形，请直接写出满足条件的点的坐标．

【答案】（1）见解析；（2）满足条件的点的坐标为或或

【详解】解：（1）如图，△即为所求；

（2）如图，满足条件的点的坐标为或或．

25．（7分）如图是一防洪堤背水坡的横截面图，斜坡的长为，它的坡角为．为了提高该堤的防洪能力，现将背水坡改造成坡度为的斜坡，在方向距点处处有一座房屋．（参考数据；

（1）求的度数；

（2）在背水坡改造的施工过程中，此处房屋是否需要拆除？

【答案】（1）；（2）在背水坡改造的施工过程中，此处房屋需要拆除

【详解】解：（1）坡度为的斜坡，

，

，

，

的坡角为，

，

；

（2），，

，

，

解得：，

故（米，

，

在背水坡改造的施工过程中，此处房屋需要拆除．

26．（8分）正方形的边长为4．

（1）将正方形对折，折痕为，如图①把这个正方形展平，再将点折到折痕上的点的位置，折痕为，交于，求的长；

（2）如图②当时，在点由点移动到中点的过程中，求面积的取值范围．

【答案】（1）；（2）

【详解】解：（1）如图①，连接，

正方形对折，折痕为，

是的垂直平分线，

，

由折叠可知：，

，

是等边三角形，

，

，

，

；

（2）如图②，作正方形的外接圆，连接，，

，

当点由点移动到中点的过程中，点在上运动，

正方形的边长为4，

正方形的对角线为，

，

过点作于点，

，

当点与点（C）重合时，点到的距离最短，为，

此时，

当，，三点共线时，点到的距离最长，为，

此时，

面积的取值范围是．

27．（9分）如图，在平面直角坐标系中，二次函数的图象交轴于点、，交轴于点，其顶点为，已知，，．

（1）求二次函数的表达式及其顶点的坐标；

（2）点是线段上方抛物线上的一个动点，点是线段上一点，当的面积最大时，求：

①点的坐标，说明理由；

②的最小值 　　；

（3）在二次函数的图象上是否存在点，使得以点、、为顶点的三角形为直角三角形？若存在，求出点坐标；若不存在，请说明理由．

【答案】（1），；（2）①，，②；（3）存在，点坐标为，或，

【详解】解：（1），

，

，，

，，

，

，，，

将、、代入中，

，

解得，

，

，

；

（2）①设的解析式为，

，

解得，

，

过点作轴交于点，

设，则，

，

，

，

当时，有最大值，

此时，；

②过点作轴交于，交于，

，

，

，

，，

，

的最小值为，

故答案为：；

（3）存在点，使得以点、、为顶点的三角形为直角三角形，理由如下：

设，

如图2，当时，

过点作轴，过点作交于，过点作交于，

，

，

，

，

，

，

解得（舍或，

，；

如图3，当时，过点作轴，过点作交于，过点作交于，

，，

，

，

，

，

解得（舍或，

，；

综上所述：点坐标为，或，．

28．（12分）如图①，等边三角形纸片中，，点在上，，过点折叠该纸片，得点和折痕（点不与点、重合）．

（1）当点落在上时，依题意补全图②，求证：；

（2）设的面积为，是否存在最小值？若存在，求出的最小值；若不存在，请说明理由；

（3）当，，三点共线时，的长为 　　

【答案】（1）见解析；（2）存在最小值，（3）

【详解】（1）证明：补全图形，如图②所示，

是等边三角形，

，

过点折叠该纸片，得点和折痕，

，

，

；

（2）解：存在最小值，

如图③，过点作于，

是等边三角形，

，，

又，

，

由折叠可知，，

点在以为圆心，4为半径的圆上，

当点在上时，点到的距离最小，最小，

中，，

；

（3）解：，理由如下：

如图④，连接，过点作于点，过点作于点，

则，

设，

由翻折得：，，，

，，

，，

，

，，三点共线，

，，

，

，

即：

，

，

，

，

的长为，

故答案为：．