






还剩37页未读,
继续阅读
所属成套资源:高中数学同步课件必修第一册课件(新教材)
成套系列资料,整套一键下载
高中数学新教材必修第一册 第3章 章末复习课课件PPT
展开
这是一份高中数学新教材必修第一册 第3章 章末复习课课件PPT,共45页。
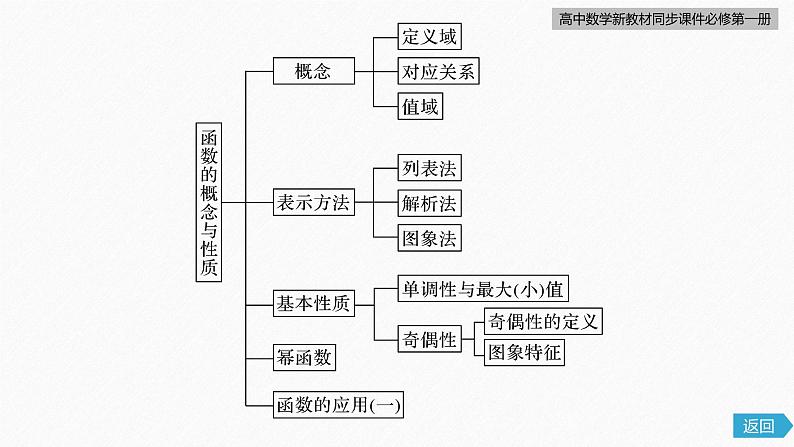
高中数学新教材 同步课件(必修第一册)章末复习课第三章 函数的概念与性质一、求函数的定义域、值域二、函数的图象三、函数的性质内容索引知识网络随堂演练四、函数的应用知识网络一、求函数的定义域、值域1.求函数定义域的常用依据是分母不为0,偶次根式中被开方数大于或等于0等,由几个式子构成的函数,其定义域是使各式子有意义的集合的交集;函数的值域是在函数的定义域下函数值的取值范围,一般是利用函数的图象或函数的单调性求值域.2.掌握集合的运算,解简单的不等式,提升逻辑推理和数学抽象素养.√√解析 由y=f(x-1)的定义域是[-1,2],得x-1∈[-2,1],即f(x)的定义域是[-2,1],令-2≤1-3x≤1,解得0≤x≤1,即y=f(1-3x)的定义域为[0,1].反思感悟 求函数定义域的类型与方法(1)已给出函数解析式:函数的定义域是使解析式有意义的自变量的取值集合.(2)常见求定义域的形式:根式,根号下非负;分式,分母不为0;0次幂,底数不为0.(3)复合函数问题:①若f(x)的定义域为[a,b],f(g(x))的定义域应由a≤g(x)≤b解出;②若f(g(x))的定义域为[a,b],则f(x)的定义域为g(x)在[a,b]上的值域.注意:①f(x)中的x与f(g(x))中的g(x)地位相同;②定义域所指永远是x的范围.跟踪训练1 (1)若函数y=f(x)的定义域是[-2,4],则函数g(x)=f(-x)的定义域是A.[-4,4] B.[-4,2] C.[-4,-2] D.[2,4]解析 由-2≤-x≤4,得-4≤x≤2.所以函数g(x)=f(-x)的定义域是[-4,2].√故函数的定义域是{x|1≤x≤5且x≠3}.{x|1≤x≤5且x≠3}二、函数的图象1.会根据函数的解析式及性质判断函数的图象,利用函数的图象可以直观观察函数值域、最值、单调性、奇偶性等,重点是一次函数、二次函数、反比例函数及幂函数图象.2.掌握简单的基本函数图象,提升直观想象和数据分析素养.例2 已知函数f(x)=|-x2+2x+3|.(1)画出函数图象并写出函数的单调区间;解 当-x2+2x+3≥0,即-1≤x≤3时,函数f(x)=-x2+2x+3=-(x-1)2+4,当-x2+2x+3<0,即x<-1或x>3时,函数f(x)=x2-2x-3=(x-1)2-4,单调递增区间为[-1,1]和[3,+∞),单调递减区间为(-∞,-1)和(1,3).(2)求集合M={m|使方程f(x)=m有四个不相等的实数根}.解 由题意可知,函数y=f(x)与y=m的图象有四个不同的交点,则0<m<4.故集合M={m|0x2,则因为x1>x2>1,所以x1-x2>0,x1x2-1>0,x1x2>0,所以f(x1)-f(x2)>0,即f(x1)>f(x2),所以函数f(x)在(1,+∞)上单调递增.(3)在(2)的条件下,若实数m满足f(3m)>f(5-2m),求m的取值范围.解 由(2)知函数f(x)在(1,+∞)上单调递增,所以3m>5-2m>1,解得11,x1x2-1>0,∴f(x1)-f(x2)<0,即f(x1)20时,年销售总收入为260万元.记该工厂生产并销售这种产品所得的年利润为y万元.(年利润=年销售总收入一年总投资)(1)求y(万元)与x(件)的函数关系式;解 由题意得,当x≤20时,y=(33x-x2)-x-100=-x2+32x-100,当x>20时,y=260-100-x=160-x,(2)当该工厂的年产量为多少件时,所得年利润最大?最大年利润是多少?解 当020时,160-x<140,故当年产量为16件时,所得年利润最大,最大年利润为156万元.反思感悟 能够将实际问题转化为熟悉的函数模型,特别注意实际问题与自变量取值范围的联系.解 当甲投入25万元时,乙投入55万元,故甲、乙两个项目的总收益为92.5万元.(2)问甲、乙两个项目各投入多少万元时,总收益最大?解 设甲投入x万元,则乙投入(80-x)万元,∴当x=36时,f(x)的最大值为92,综上,当x=25时,f(x)的最大值为92.5,故甲、乙两个项目分别投入25万元、55万元时,总收益最大.随堂演练1234√1234√1234则f(x)的定义域为R,所以函数为奇函数,排除C,D.1234√1234164.设某公司原有员工100人从事产品A的生产,平均每人每年创造产值t万元(t为正常数).公司决定从原有员工中分流x(0
高中数学新教材 同步课件(必修第一册)章末复习课第三章 函数的概念与性质一、求函数的定义域、值域二、函数的图象三、函数的性质内容索引知识网络随堂演练四、函数的应用知识网络一、求函数的定义域、值域1.求函数定义域的常用依据是分母不为0,偶次根式中被开方数大于或等于0等,由几个式子构成的函数,其定义域是使各式子有意义的集合的交集;函数的值域是在函数的定义域下函数值的取值范围,一般是利用函数的图象或函数的单调性求值域.2.掌握集合的运算,解简单的不等式,提升逻辑推理和数学抽象素养.√√解析 由y=f(x-1)的定义域是[-1,2],得x-1∈[-2,1],即f(x)的定义域是[-2,1],令-2≤1-3x≤1,解得0≤x≤1,即y=f(1-3x)的定义域为[0,1].反思感悟 求函数定义域的类型与方法(1)已给出函数解析式:函数的定义域是使解析式有意义的自变量的取值集合.(2)常见求定义域的形式:根式,根号下非负;分式,分母不为0;0次幂,底数不为0.(3)复合函数问题:①若f(x)的定义域为[a,b],f(g(x))的定义域应由a≤g(x)≤b解出;②若f(g(x))的定义域为[a,b],则f(x)的定义域为g(x)在[a,b]上的值域.注意:①f(x)中的x与f(g(x))中的g(x)地位相同;②定义域所指永远是x的范围.跟踪训练1 (1)若函数y=f(x)的定义域是[-2,4],则函数g(x)=f(-x)的定义域是A.[-4,4] B.[-4,2] C.[-4,-2] D.[2,4]解析 由-2≤-x≤4,得-4≤x≤2.所以函数g(x)=f(-x)的定义域是[-4,2].√故函数的定义域是{x|1≤x≤5且x≠3}.{x|1≤x≤5且x≠3}二、函数的图象1.会根据函数的解析式及性质判断函数的图象,利用函数的图象可以直观观察函数值域、最值、单调性、奇偶性等,重点是一次函数、二次函数、反比例函数及幂函数图象.2.掌握简单的基本函数图象,提升直观想象和数据分析素养.例2 已知函数f(x)=|-x2+2x+3|.(1)画出函数图象并写出函数的单调区间;解 当-x2+2x+3≥0,即-1≤x≤3时,函数f(x)=-x2+2x+3=-(x-1)2+4,当-x2+2x+3<0,即x<-1或x>3时,函数f(x)=x2-2x-3=(x-1)2-4,单调递增区间为[-1,1]和[3,+∞),单调递减区间为(-∞,-1)和(1,3).(2)求集合M={m|使方程f(x)=m有四个不相等的实数根}.解 由题意可知,函数y=f(x)与y=m的图象有四个不同的交点,则0<m<4.故集合M={m|0
相关资料
更多









