北师大版数学八年级上册《平行线的证明》全章复习与巩固(提高)知识讲解 (含答案)

《平行线的证明》全章复习与巩固（提高）知识讲解

【学习目标】

1．   了解定义及命题的概念与构成，并能通过证明或举反例判定命题的真假；

2. 区别平行线的判定与性质，并能灵活运用；

3. 理解并能灵活运用三角形的内角和定理及其推论.

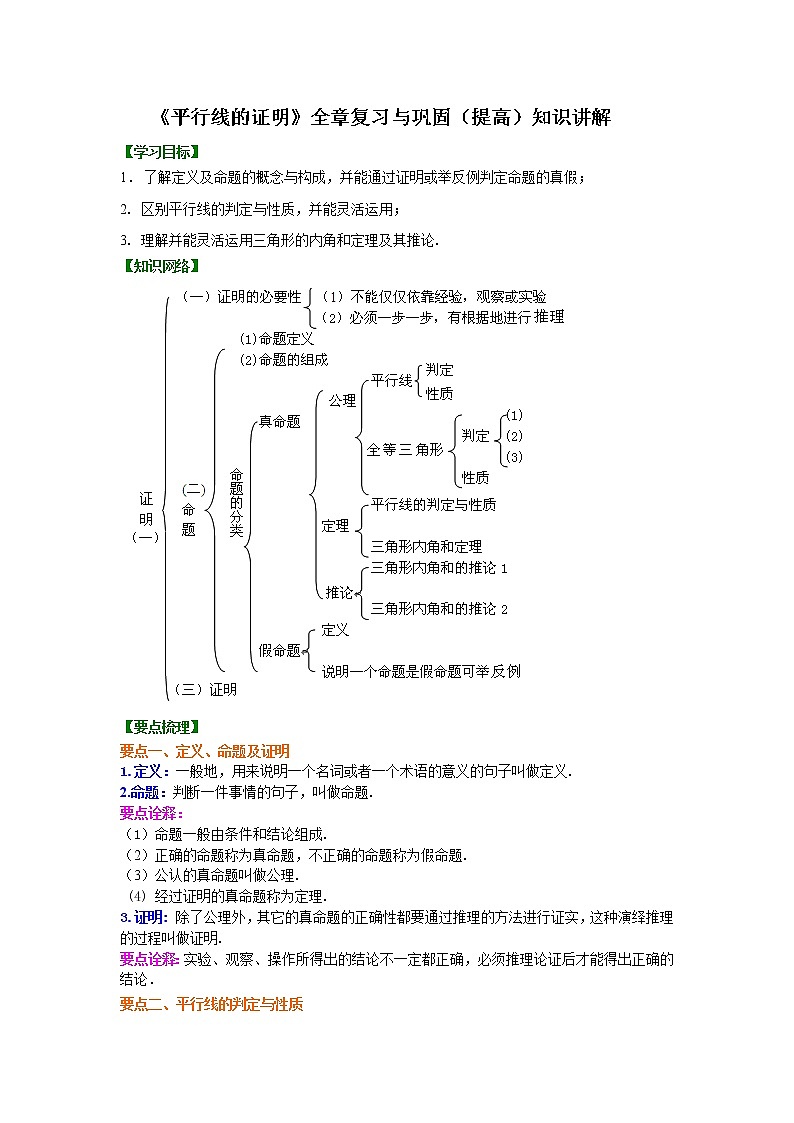
【知识网络】

【要点梳理】

要点一、定义、命题及证明

1.定义：一般地，用来说明一个名词或者一个术语的意义的句子叫做定义.

2.命题：判断一件事情的句子，叫做命题.
要点诠释：

（1）命题一般由条件和结论组成.
（2）正确的命题称为真命题，不正确的命题称为假命题.
（3）公认的真命题叫做公理.

(4) 经过证明的真命题称为定理.

3.证明: 除了公理外，其它的真命题的正确性都要通过推理的方法进行证实，这种演绎推理的过程叫做证明.
要点诠释：实验、观察、操作所得出的结论不一定都正确，必须推理论证后才能得出正确的结论．

要点二、平行线的判定与性质

1．平行线的判定

判定方法1：同位角相等，两直线平行．

判定方法2：内错角相等，两直线平行．

判定方法3：同旁内角互补，两直线平行．

要点诠释：根据平行线的定义和平行公理的推论，平行线的判定方法还有：

（1）平行线的定义：在同一平面内，如果两条直线没有交点（不相交），那么两直线平行.

（2）如果两条直线都平行于第三条直线，那么这两条直线平行（平行线的传递性）.

（3）在同一平面内，垂直于同一直线的两条直线平行.

（4）平行公理：经过直线外一点，有且只有一条直线与这条直线平行.

2．平行线的性质

性质1：两直线平行，同位角相等；

性质2：两直线平行，内错角相等；

性质3：两直线平行，同旁内角互补.

要点诠释：根据平行线的定义和平行公理的推论，平行线的性质还有：

（1）若两条直线平行，则这两条直线在同一平面内，且没有公共点．

（2）如果一条直线与两条平行线中的一条直线垂直，那么它必与另一条直线垂直．

要点三、三角形的内角和定理及推论

三角形的内角和定理：三角形的内角和等于180°．

                推论：（1）三角形的一个外角等于和它不相邻的两个内角的和．

                      （2）三角形的一个外角大于任何一个和它不相邻的内角．

要点诠释：

（1）由一个公理或定理直接推出的真命题，叫做这个公理或定理的推论.

（2）推论可以当做定理使用.

【典型例题】

类型一、定义、命题及证明

1. 我们知道任何一个命题都由条件和结论两部分组成,如果我们把一个命题的条件变结论,结论变条件,那么所得的是不是一个命题?试举例说明.

【答案与解析】

解：是一个命题,例如“对顶角相等”条件结论互换就变为“相等的角是对顶角”.

【总结升华】如果将一个命题的条件与结论互换，则得到这个命题的逆命题，但原命题正确，逆命题不一定正确.

举一反三：

【变式】下列命题中,真命题有(   ) .

①       ­若x＝a，则x2－(a+b)x+ab＝0

②       直线外一点到这条直线的垂线段，叫做这个点到这条直线的距离

③       如果 ＝0,那么x＝±2

④       如果a＝b,那么a3＝b3

­  A.1个­     B.2个­     C.3个­     D.4个

【答案】C

2.如图所示，O是直线AB上一点，射线OC、OD在AB的两侧，且∠AOC＝∠BOD，试证明∠AOC与∠BOD是对顶角．

【答案】

证明：因为∠AOC+∠COB＝180°(平角定义)，

    又因为∠AOC＝∠BOD(已知)，

    所以∠BOD+∠COB＝180°，即∠COD＝180°．

    所以C、O、D三点在一条直线上(平角定义)，

    即直线AB、CD相交于点O，

    所以∠AOC与∠BOD是对顶角(对顶角定义)．

【总结升华】证三点共线的方法，通常采用证这三点组成的角为平角，即∠COD＝180°．

类型二、平行线的性质与判定

3. （2020春•胶州市期中）将一副三角板中的两根直角顶点C叠放在一起（如图①），其中∠A=30°，∠B=60°，∠D=∠E=45°．

（1）若∠BCD=150°，求∠ACE的度数；

（2）试猜想∠BCD与∠ACE的数量关系，请说明理由；

（3）若按住三角板ABC不动，绕顶点C转动三角板DCE，试探究∠BCD等于多少度时，CD∥AB，并简要说明理由．

【思路点拨】（1）由∠BCD=150°，∠ACB=90°，可得出∠DCA的度数，进而得出∠ACE的度数；

（2）根据（1）中的结论可提出猜想，再由∠BCD=∠ACB+∠ACD，∠ACE=∠DCE﹣∠ACD可得出结论；

（3）根据平行线的判定定理，画出图形即可求解．

【答案与解析】解：（1）∵∠BCA=∠ECD=90°，∠BCD=150°，

∴∠DCA=∠BCD﹣∠BCA=150°﹣90°=60°，

∴∠ACE=∠ECD﹣∠DCA=90°﹣60°=30°；

（2）∠BCD+∠ACE=180°，理由如下：

∵∠BCD=∠ACB+∠ACD=90°+∠ACD，

∠ACE=∠DCE﹣∠ACD=90°﹣∠ACD，

∴∠BCD+∠ACE=180°；

（3）当∠BCD=120°或60°时，CD∥AB．

如图②，根据同旁内角互补，两直线平行，

当∠B+∠BCD=180°时，CD∥AB，此时∠BCD=180°﹣∠B=180°﹣60°=120°；

如图③，根据内错角相等，两直线平行，

当∠B=∠BCD=60°时，CD∥AB．

【总结升华】本题考查了平行线的判定：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行．熟练掌握定理并且能够准确识图是解题的关键．

4. （2020春•海珠区期末）如图，已知AD∥BC，∠1=∠2，求证：∠3+∠4=180°．

【思路点拨】欲证∠3+∠4=180°，需证BE∥DF，而由AD∥BC，易得∠1=∠3，又∠1=∠2，所以∠2=∠3，即可求证．

【答案与解析】

证明：∵AD∥BC，

∴∠1=∠3，

∵∠1=∠2，

∴∠2=∠3，

∴BE∥DF，

∴∠3+∠4=180°．

【总结升华】此题考查平行线的判定和性质：同位角相等，两直线平行；两直线平行，内错角相等；两直线平行，同旁内角互补．要灵活应用．

举一反三：

【变式1】（2020春•大名）如图：AD∥BC，∠DAC=60°，∠ACF=25°，∠EFC=145°，则直线EF与BC的位置关系是      　．

【答案】

解：平行．

∵AD∥BC，

∴∠ACB=∠DAC=60°，

∵∠ACF=25°，

∴∠FCB=35°，

∴∠EFC+∠FCB=145°+35°=180°，

∴EF∥BC，故答案为：平行．

【变式2】已知：如图，∠ABC＝∠ADC，BF、DE分别平分∠ABC与∠ADC，且∠1＝∠3.

求证：AB∥DC.

【答案】

证明：∵∠ABC＝∠ADC,

∴（等式性质）.

又∵BF、DE分别平分∠ABC与∠ADC,

∴∠1＝，∠2＝（角平分线的定义）.

∴∠1＝∠2　（等量代换）.

又∵∠1＝∠3（已知）,

∴∠2＝∠3（等量代换）.

∴AB∥DC(内错角相等，两直线平行).

类型三、三角形的内角和定理及推论

5.如图，P是△ABC 内一点，请用量角器量出∠ABP.∠ACP.∠A和∠BPC的大小，再计算一下，∠ABP＋∠ACP＋∠A是多少度？这三个角的和与∠BPC有什么关系？你能用学到的知识来解释其中的道理吗？你能判断∠BPC和∠A的大小吗？

【答案与解析】

解：∠ABP＋∠ACP＋∠A＝∠BPC，∠BPC＞∠A。

证明：如下图，延长BP到D，

则∠PDC＝∠A＋∠∠ABP，∠PDC>∠A.

 同理，∠BPC＝∠PDC＋∠ACP，∠BPC>∠PDC.

所以∠BPC＝∠ABP＋∠ACP＋∠A ，∠BPC＞∠A .

举一反三：

【变式1】如图,△ABC的两外角平分线交于点P,易证∠P＝90°-∠A；△ABC两内角的平分线交于点Q,易证∠BQC＝90°+∠A；那么△ABC的内角平分线BM与外角平分CM的夹角

∠M＝_____∠A.

【答案】

【变式2】如图,E是BC延长线上的点,∠1＝∠2.求证:∠BAC＞∠B.

【答案】

证明：∵∠2＝∠B+∠D

­      ∴∠B＝∠2-∠D

­    又∵∠BAC＝∠1+∠D  ∠1＝∠2

­      ∴∠BAC>∠B

类型四、实际应用

6.手工制作课上，老师先将一张长方形纸片折叠成如图所示的那样，若折痕与一条边BC的夹角∠EFB＝30°，你能说出∠EGF的度数吗？

【思路点拨】长方形的对边是平行的，所以AD∥BC，可得∠DEF＝∠EFG＝30°，又因为折后重合部分相等，所以∠GEF＝∠DEF＝30°，所以∠DEG＝2∠DEF＝60°，又因为两直线平行，同旁内角互补，所以∠EGC＝180°－∠DEG，问题可解.

【答案与解析】

解：因为AD∥BC（已知），

所以∠DEF＝∠EFG＝30°（两直线平行，内错角相等）.

因为∠GEF＝∠DEF＝30°（对折后重合部分相等），

所以∠DEG＝2∠DEF＝60°.

所以∠EGC＝180°－∠DEG＝180°－60°＝120°（两直线平行，同旁内角互补）.

【总结升华】本题利用了：（1）折叠的性质：折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等；（2）平行线的性质．