数学4.4 角说课ppt课件

教学目标

1.会比较两个角的大小.

2.理解角的和差,在操作活动中认识角的平分线.

3.通过实际观察、操作、体会角的大小,并简单说理,培养学生的观察思维能力及合情推理能力.

教学重难点

重点:角的大小比较方法以及角平分线的概念.

难点:理解角的和差以及角平分线的概念.

教学过程

导入新课

【问题】我们是如何比较两条线段的长短的?

1.测量法,分别量出两条线段的长度,然后再比较大小.

2.叠合法,把两条线段叠合在一起比较大小.

要如何比较两个角的大小呢？

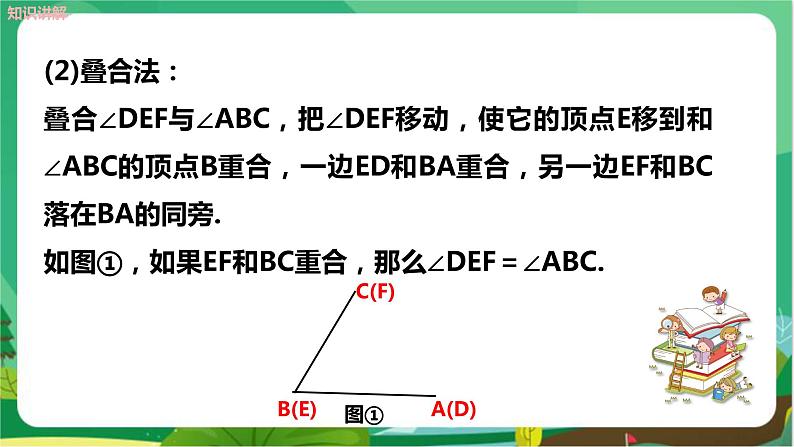
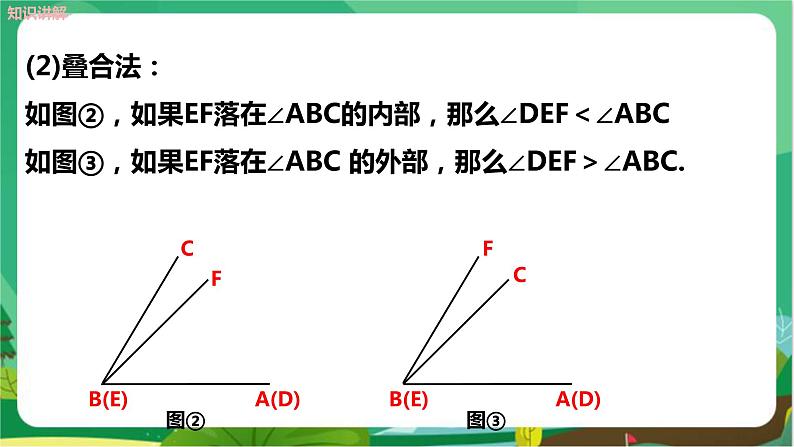
探究新知

【活动1】角的大小比较

如图,如何比较两角∠BAC与∠EDF的大小呢?

【互动】学生回答，教师引导总结角的大小比较的两种方法:

1.度量法:即用量角器量出角的度数,通过比较角的度数来比较角的大小,度数大的角大,度数小的角小.

2.叠合法:即把两个角叠合在一起(使两角的顶点和它们的一边重合在一起)进行比较.

师:用叠合法比较角的大小有哪几种情况呢?

(1)    AB在∠FED的内部，∠ABC<∠FED.

(2)    AB在∠FED的外部，∠ABC>∠FED.

(3)      AB与EF重合，∠ABC=∠FED.

【思考】按角的大小来分,还记得我们可以把角分成哪几类吗?

教师引导学生回答.

锐角:小于直角的角,如∠1.

直角:等于90°的角，如∠2.

钝角:大于直角而小于平角的角,如∠3.

【活动2】角的平分线

师:你能说出图中有几个角吗?它们有什么关系呢?

生:∠1+∠2＝∠3,∠1＝∠3-∠2,∠2＝∠3-∠1.

师:如果图中的∠1与∠2相等,它们又有什么关系?

生:∠3＝2∠1＝2∠2,∠1＝∠2＝∠3.

师:从一个角的顶点出发,把一个角分成相等的两个角的射线叫做这个角的平分线(也叫做角的二等分线).类似的,还有三等分线、四等分线等.

【例】如图所示,求解下列问题:

(1)比较∠AOC与∠BOC、∠BOD与∠COD的大小;

(2)将∠AOC写成两个角的和与两个角的差的形式.

【解】(1)由图可以看出:∠AOC>∠BOC,(OB在∠AOC内),

∠BOD>∠COD.(OC在∠BOD内)

(2)∠AOC=∠AOB+∠BOC,∠AOC=∠AOD-∠DOC.

课堂练习

1.根据图1填空：

①∠AOB＝∠AOC+∠_____；

②∠AOD＝∠AOB-∠____ ＝∠_____ -∠COD；

③∠AOC+∠BOD-∠AOB＝________.

2.如图2，∠ABC＝90°，∠CBD＝30°，BP平分∠ABD. 求∠ABP的度数.

参考答案

1.∠BOC，∠BOD，∠AOC，∠COD

2.解：∵ ∠ABC＝90°，∠CBD＝30°，

  ∴ ∠ABD＝∠ABC+∠CBD＝120°.

又∵ BP平分∠ABD，

  ∴ ∠ABP＝∠ABD＝60°.

课堂小结

通过这节课的学习，你有哪些收获？

1. 角的大小的比较方法：

(1)度量法；(2)叠合法.

2. 角平分线的定义及性质：

在角的内部，以角的顶点为端点的一条射线把这个角分成两个相等的角，这条射线叫做这个角的平分线.若OC是∠AOB的平分线，则∠AOC＝∠COB＝∠AOB，∠AOB＝2∠AOC＝2∠COB.

布置作业

课本P150习题4.5第1，2，3题.

板书设计

4.5　角的比较与补（余）角

第1课时　比较角的大小

     一、角的大小比较   

1.度量法   2.叠合法

二、角的平分线

1.角的和差 2.角的平分线

教学反思

教学反思

教学反思