初中数学人教版八年级下册18.1.1 平行四边形的性质精品ppt课件

这是一份初中数学人教版八年级下册18.1.1 平行四边形的性质精品ppt课件，共19页。PPT课件主要包含了对角相等邻角互补，对边平行且相等，平行线之间的距离，知识要点1，平行四边形的性质3，∴OEOF，对角线，对角线互相平分，线段相等，面积关系等内容，欢迎下载使用。

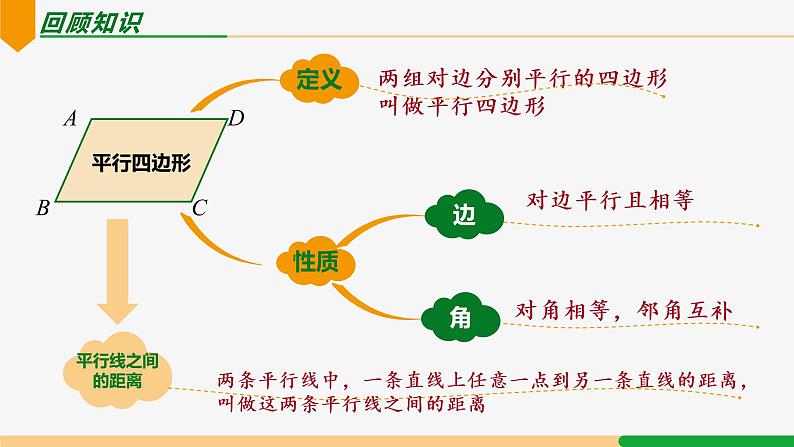
两组对边分别平行的四边形叫做平行四边形
两条平行线中，一条直线上任意一点到另一条直线的距离，叫做这两条平行线之间的距离.
1.判断题(对的在括号内填“ √ ”，错的填“×”)： (1)平行四边形两组对边分别平行且相等. ( ) (2)平行四边形的四个内角都相等. ( ) (3)平行四边形的相邻两个内角的和等于 180°. ( ) (4)如果平行四边形相邻两边长分别是 2 cm 和 3 cm，那么周长是 10 cm. ( ) (5)在平行四边形 ABCD 中，如果∠A = 42°，那么∠B = 48°. ( ) (6)在平行四边形 ABCD 中，如果∠A = 35°，那么∠C = 145°. ( )
一位饱经沧桑的老人，经过一辈子的辛勤劳动，到晚年的时候，终于拥有了一块平行四边形的土地，由于年迈体弱，他决定把这块土地分给他的四个孩子，他是这样分的：
当四个孩子看到时，争论不休，都认为自己分的地少，同学们，你认为老人这样分合理吗?为什么?
思考 第十八章 平行四边形思考下列问题.
问题1 本章平行四边将学习哪些内容？
问题2 平行四边与之前学习过的哪些知识有联系？将怎样去学习呢？
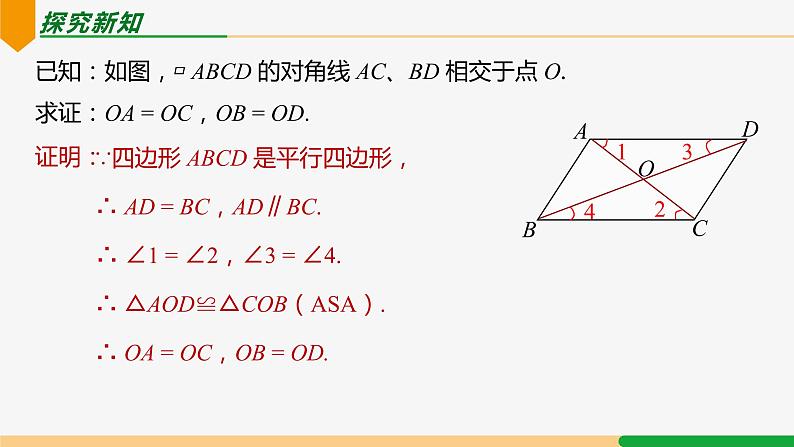
已知：如图，▱ ABCD 的对角线 AC、BD 相交于点 O.求证：OA = OC，OB = OD.
∵四边形 ABCD 是平行四边形，
∴ AD = BC，AD∥BC.
∴ ∠1 = ∠2，∠3 = ∠4.
∴ △AOD≌△COB（ASA）.
∴ OA = OC，OB = OD.
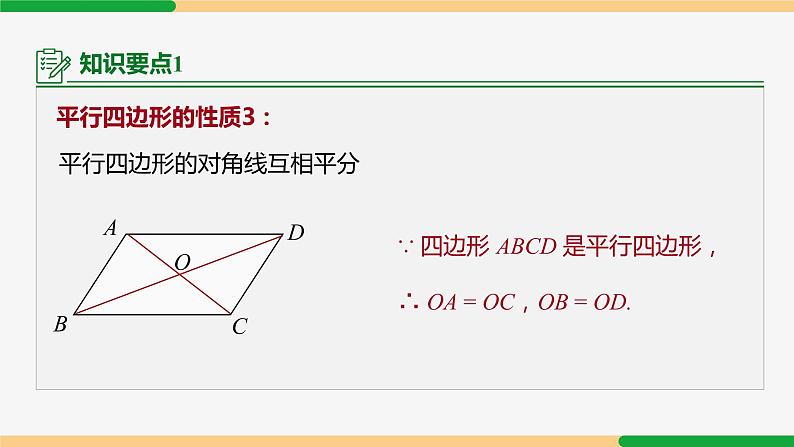
平行四边形的对角线互相平分
∵ 四边形 ABCD 是平行四边形，
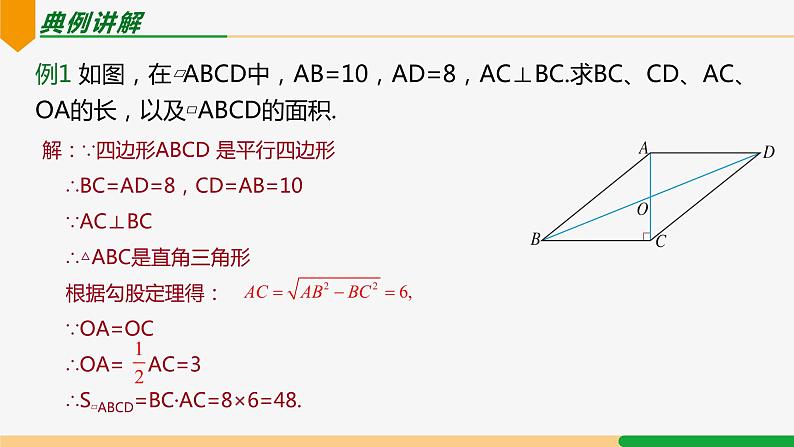
例1 如图，在▱ABCD中，AB=10，AD=8，AC⊥BC.求BC、CD、AC、OA的长，以及▱ABCD的面积.
解：∵四边形ABCD 是平行四边形 ∴BC=AD=8，CD=AB=10 ∵AC⊥BC ∴△ABC是直角三角形 根据勾股定理得： ∵OA=OC ∴OA= AC=3 ∴S▱ABCD=BC·AC=8×6=48.
解：设 AB = x，则 BC = 24 - x.根据平行四边形的面积公式可得5x = 10 ( 24 - x )，解得 x = 16．则平行四边形 ABCD 的面积为 5×16 = 80．
例2 如图，平行四边形 ABCD 中，DE⊥AB 于 E，DF⊥BC 于 F，若平行四边形 ABCD 的周长为 48，DE = 5，DF = 10，求平行四边形 ABCD 的面积.
例3 如图，▱ ABCD 的对角线 AC，BD 交于点O. 过点 O作直线 EF，分别交 AB，CD 于点 E，F. 求证：OE=OF.
证明：∵ 四边形 ABCD 是平行四边形，
∴∠ODF = ∠OBE， ∠DFO = ∠BEO，
∴△DOF≌△BOE(AAS)，
∴ AB∥CD， OD = OB，
请判断下列图中，OE = OF 还成立么？
过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交，得到的线段总相等.
∴S四边形ANMB = S△NAO+S△AOB+S△MOB = S△MCO+S△AOB+S△MOB =S△AOB + S△COB = .∴ S四边形ANMB = S四边形CMND.即平行四边形 ABCD 被 EF 所分的两个四边形面积相等.
例4 如图，AC，BD 交于点 O，EF 过点 O，平行四边形 ABCD 被 EF 所分的两个四边形面积相等吗？
解：设直线 EF 交 AD，BC 于点 N，M.
∵AD∥BC，∴∠NAO =∠MCO，∠ANO =∠CMO.
又∵ AO = CO，
∴△NAO≌△MCO.
1.如图，平行四边形 ABCD 的对角线 AC，BD 交于点 O，若AD =16，AC=24，BD=12，则△OBC的周长为(　　)A. 26 B. 34 C. 40 D. 52
2.如图，在▱ABCD 中，对角线 AC 和 BD 相交于点 O，△AOB 的周长为 15，AB = 6，则对角线 AC、BD 的长度的和是 (　　) A. 9 B. 18 C. 27 D. 36
3.在□ABCD 中，AC = 24，BD = 38，AB = m，则 m 的取值范围是 ( ) A. 24＜m＜39 B. 14＜m＜62 C. 7＜m＜31 D. 7＜m＜12
4.如图，▱ABCD 的对角线 AC，BD 相交于 O，EF 过点 O 与 AD，BC 分别相交于E，F，如果 AB = 4，BC = 5，OE = 1.5，那么四边形 EFCD 的周长为(　　) A. 16 B. 14 C. 12 D. 10
5 已知 ▱ABCD 的周长为 60 cm，对角线 AC、BD 相交于点 O，△AOB 的周长比△DOA 的周长长 5 cm，求这个平行四边形各边的长．
解：∵四边形 ABCD 是平行四边形，∴OB＝OD，AB＝CD，AD＝BC.∵△AOB 的周长比△DOA 的周长长 5 cm，∴ AB－AD＝5 cm.又∵ ▱ ABCD 的周长为 60 cm，∴ AB＋AD＝30 cm，则 AB＝CD＝17.5cm，AD＝BC＝12.5 cm.
解：BE＝DF，BE∥DF.理由如下：∵ 四边形 ABCD 是平行四边形，∴ OA＝OC，OB＝OD，∴ OE＝OF.在△OFD 和△OEB 中，OF＝OE，∠DOF＝∠BOE，OD＝OB， ∴△OFD≌△OEB (SAS)，∴∠OEB＝∠OFD，BE＝DF.∴ BE∥DF.
6. 如图，平行四边形 ABCD 中，AC、BD 交于O点，点 E、F 分别是 AO、CO 的中点，试判断线段 BE、DF 的关系并证明你的结论．
7.如图，平行四边形 ABCD 的对角线相交于点 O，且 AB ≠ AD，过 O 作 OE⊥BD，交 BC 于点 E. 若△CDE 的周长为 10，则平行四边形 ABCD 的周长是多少？
解：∵ 四边形 ABCD 是平行四边形，∴ AB = CD，BC = AD，OB = OD.∵ OE⊥BD，∴ BE = DE.∵△CDE 的周长为10，∴ DE + CE + CD = BE + CE + CD = BC + CD = 10.∴平行四边形 ABCD 的周长为 2×(BC + CD) = 20．