
《正态分布》示范课教案【高中数学苏教版】
展开第八章 概率
8.2.3 正态分布
1.认识正态分布曲线的特点和性质及曲线表示的意义。
2.会根据对称性进行简单正态分布的相关概率计算,并能解决一些简单的实际问题。
3.能用正态分布、正态曲线研究有关随机变量分布的规律,通过观察并探究规律,提高分析问题,解决问题的能力。
4.会查标准正态分布表,求满足标准正态分布的随机变量X在某一个范围内的概率。
重点:认识正态分布曲线的特点和性质及曲线表示的意义。
难点:现实生活中,什么样的随机变量服从正态分布;正态分布曲线的特点和性质以及曲线表示的意义。
一、新课导入
旧知回顾:
问题:前面我们学习了两点分布、二项分布、超几何分布,它们的随机变量有什么共同点?
答案:它们都是离散型随机变量。
师提问:生产生活当中还有其它类型的随机变量吗?举例说明。
答案:二项分布、超几何分布是刻画离散型随机变量分布的数学模型,在实际应用中,还有许多随机变量可以取某一区间中的一切值,这类随机变量就是连续型随机变量 (continuous randomvariable)。比如,某种产品的使用寿命X是一个随机变量,它可以取区间或内的所有值。
师引出本节课题:《正态分布》。
设计意图:复习回顾两点分布、二项分布、超几何分布,为引出正态分布做铺垫。
二、新知探究
思考:现给出一组金属长度的样本数据如下:
6.02 | 6.01 | 6.04 | 5.94 | 5.97 | 5.96 | 5.98 | 6.01 | 5.98 | 6.02 |
6.00 | 6.03 | 6.07 | 5.97 | 6.01 | 6.00 | 6.03 | 5.95 | 6.00 | 6.00 |
6.05 | 5.93 | 6.02 | 5.99 | 6.00 | 5.95 | 6.00 | 5.97 | 5.96 | 5.97 |
6.03 | 6.01 | 6.00 | 5.99 | 6.04 | 6.00 | 6.02 | 5.99 | 6.03 | 5.98 |
用什么数学知识能够准确直观地研究数据的分布情况?
答案:根据这些数据作出频率分布直方图。
学生尝试解决问题。
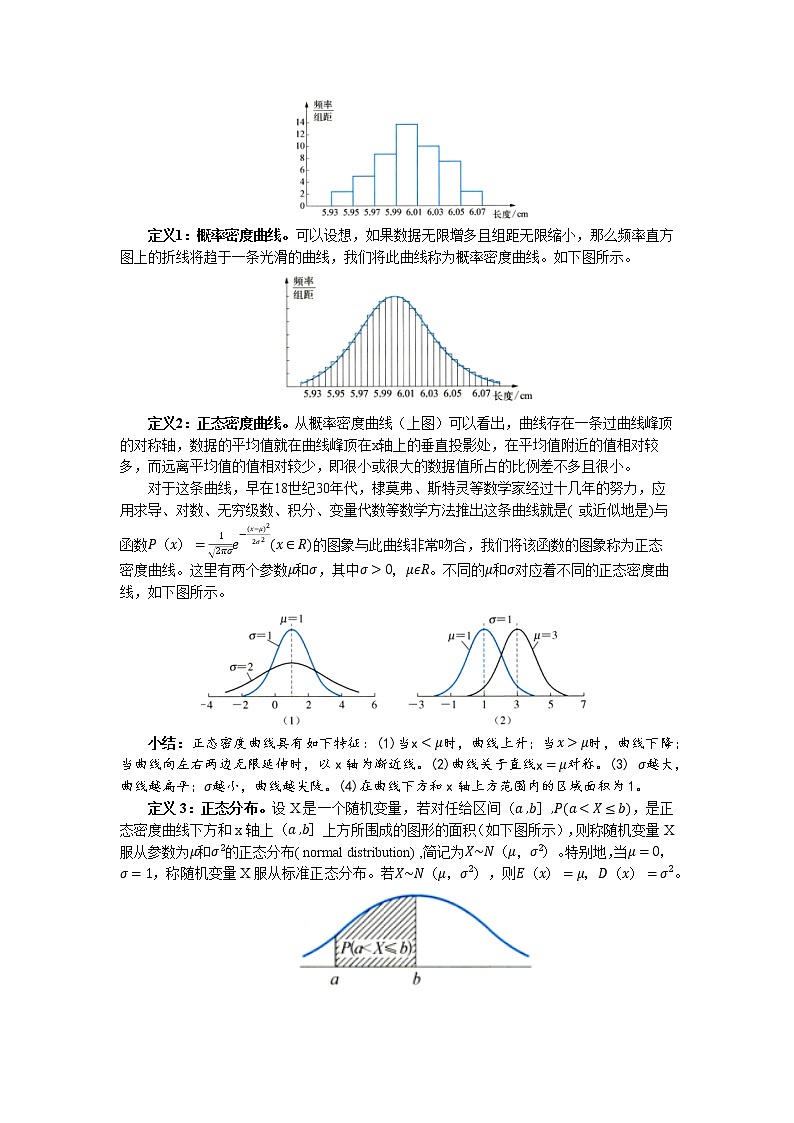
分析:第一,对数据进行分组(组距为0.02);第二,列出频数分布表;第三,作出频率分布直方图(如下图所示)。这个直方图大体呈中间高、两边低、左右大致对称的特点。如果增加更多的测量数据,那么这种趋势会更加明显。
定义1:概率密度曲线。可以设想,如果数据无限增多且组距无限缩小,那么频率直方图上的折线将趋于一条光滑的曲线,我们将此曲线称为概率密度曲线。如下图所示。
定义2:正态密度曲线。从概率密度曲线(上图)可以看出,曲线存在一条过曲线峰顶的对称轴,数据的平均值就在曲线峰顶在x轴上的垂直投影处,在平均值附近的值相对较多,而远离平均值的值相对较少,即很小或很大的数据值所占的比例差不多且很小。
对于这条曲线,早在18世纪30年代,棣莫弗、斯特灵等数学家经过十几年的努力,应
用求导、对数、无穷级数、积分、变量代数等数学方法推出这条曲线就是( 或近似地是)与
函数的图象与此曲线非常吻合,我们将该函数的图象称为正态密度曲线。这里有两个参数和,其中。不同的和对应着不同的正态密度曲线,如下图所示。
小结:正态密度曲线具有如下特征:(1)当时,曲线上升;当时,曲线下降;当曲线向左右两边无限延伸时,以x轴为渐近线。(2)曲线关于直线对称。(3) 越大,曲线越扁平;越小,曲线越尖陡。(4)在曲线下方和x轴上方范围内的区域面积为1。
定义3:正态分布。设X是一个随机变量,若对任给区间,是正态密度曲线下方和x轴上上方所围成的图形的面积(如下图所示),则称随机变量X服从参数为和的正态分布( normal distribution) ,简记为。特别地,当,称随机变量X服从标准正态分布。若,则。
思考:现实世界中哪些现象遵循正态分布?
答案:例如,反复测量某个物理量,其测量误差X通常服从正态分布;某一地区同性别同年龄组儿童的体重W近似地服从正态分布;某一地区成年人的身高近似地服从正态分布;某地每年1月份的平均气温T也可认为近似地服从正态分布。
正态分布原则:假设,则随机变量X在的附近取值的概率很大,在离很远处取值的概率很小。具体如图所示:
落在区间内的概率约为68.3%;落在区间内的概率约为95.4%;落在区间内的概率约为99.7%.
在实际应用中,通常认为服从于正态分布的随机变量X只取中的值,这在统计学中称为原则。
设计意图: 借助频率分布直方图更加准确、直观、形象地研究数据的分布规律,为正态曲线的得出作铺垫。对高中生来说,正态分布密度函数的推导是十分困难的。因此,从数学史的角度介绍正态分布密度曲线的解析式,既使学生易于接受又渗透了数学的文化价值。结合正态密度函数及曲线研究了正态分布的性质。
三、应用举例
例1:已知随机变量,查标准正态分布表,求:
(1); (2);
(3);(4) 。
解 (1)=0.9357.
(2).
(3)
(4).
例2:某批待出口的水果罐头,每罐净重X(单位:g)服从正态分布,求:(1)随机抽取1罐,其净重超过184.5 g的概率;
(2)随机抽取1罐,其净重在179g与189g之间的概率。
解(1)
(2)
答 随机抽取1罐,其净重超过184.5g的概率是0.420 7,净重在179g与189 g之间的概率为0. 954 4。
小结 在实际生活中遇到的很多随机现象,随机变量大体满足其取值以某个值为中心且左右对称这种特性,一般都可以尝试用正态分布来描述这个随机变量的取值规律。
设计意图:通过举例分析,在具体的问题中体会数学在实际生活中的应用,深化了学生对正态曲线的特点及正态分布密度函数表达式中参数与的理解。
四、课堂练习
1. 判断正误(正确的打“”,错误的打“”)
(1) 正态曲线的解析式中参数, 的意义分别是样本的均值与方差。( )
(2) 服从正态分布的随机变量是连续型随机变量。( )
(3) 正态曲线是一条钟形曲线。 ( )
(4) 离散型随机变量的概率分布规律用分布密度曲线描述,连续型随机变量的概率分布用分布列描述。( )
2. 已知随机变量若,求的值。
3. 设随机变量,若,求实数a的值。
参考答案:
1.(1)(2)(3)(4)
解析:由正态分布的定义、特征和性质得知。
2. 0.8
解析:由题意可得,=0.3.因为随机变量,故
3.
解析:由正态分布的对称性及已知得出:,解得
五、课堂小结
1. 正态曲线定义、特征及性质;
2. 正态分布定义和应用;
3.原则.
六、布置作业
教材第135页习题第1、2题,第137页思考·运用第3、5题。









