初中数学6.1.1平均数授课ppt课件

这是一份初中数学6.1.1平均数授课ppt课件，共26页。PPT课件主要包含了情境引入，加权平均数，一起来看看下面的例子，合作探究，平均数更大，典例精析，议一议，做一做，期中30%，期末60%等内容，欢迎下载使用。

超市中有各种各样的苹果，每种苹果的价格都不一样，如果小明的妈妈买了 3.5 元/千克的苹果 1 千克，买了 6 元/千克的苹果 3 千克，那么小明妈妈所买苹果的平均价格是两种单价相加除以 2 吗？为什么？
在实际问题中，一组数据里的各个数据的“重要程度”未必相同，因而，在计算这组数据的平均数时，往往给每个数据一个“权”．
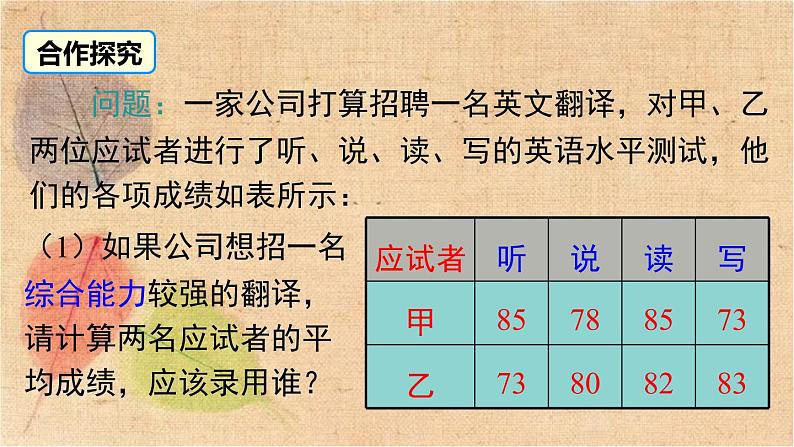
问题：一家公司打算招聘一名英文翻译，对甲、乙两位应试者进行了听、说、读、写的英语水平测试，他们的各项成绩如表所示：
（1）如果公司想招一名综合能力较强的翻译，请计算两名应试者的平均成绩，应该录用谁？
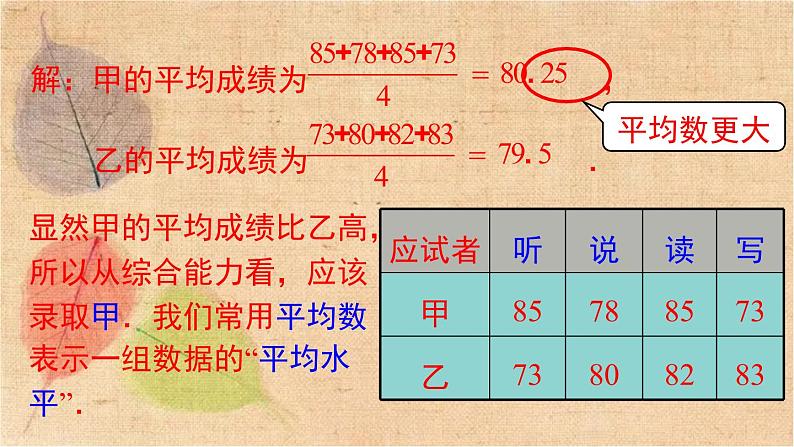
显然甲的平均成绩比乙高，所以从综合能力看，应该录取甲．我们常用平均数表示一组数据的“平均水平”．
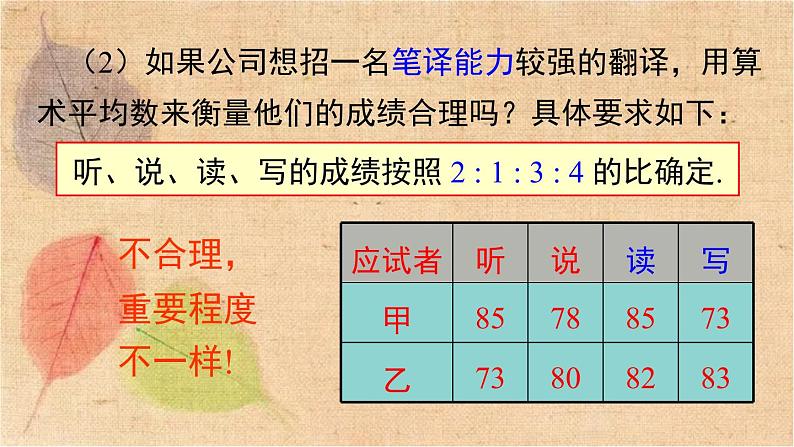
　（2）如果公司想招一名笔译能力较强的翻译，用算术平均数来衡量他们的成绩合理吗？具体要求如下：
听、说、读、写的成绩按照 2 : 1 : 3 : 4 的比确定.
不合理，重要程度不一样!
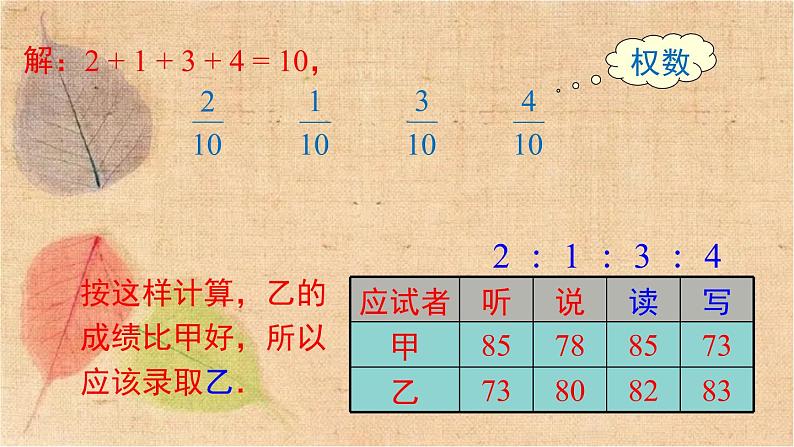
2 : 1 : 3 : 4
按这样计算，乙的成绩比甲好，所以应该录取乙．　　
先计算权数，即各数在数据组中的占比，再计算平均数，即
思考：能把这种平均数的计算方法推广到一般吗？
用这种方法求出来的平均数称为加权平均数.
（3）如果公司想招一名口语能力较强的翻译，则应该录取谁？具体要求如下：
听、说、读、写的成绩按照 3 : 3 : 2 : 2 的比确定.
同样一张应试者的应聘成绩单，由于各个数据所赋的权数不同，造成最终成绩截然不同.
（4）将问题（1）（2）（3）比较，你能体会到权的作用吗？
例1 一次演讲比赛中，评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分，各项成绩均按百分制，然后再按演讲内容占 50％、演讲能力占 40％、演讲效果占 10％的比例，计算选手的综合成绩（百分制）.
进入决赛的前两名选手的单项成绩如表所示，请决出两人的名次.
由上可知选手 B 获得第一名，选手 A 获得第二名．
你能说说平均数与加权平均数的区别和联系吗？
2. 在实际问题中，各项的权数不相等时，计算平均数时就要采用加权平均数；当各项权数相等时，直接计算算术平均数就可以了.
1. 平均数可以看做是加权平均数的一种特殊情况（它特殊在各项的权数相等）；
在 2022 年某大学数科院的研究生入学考试中，两名考生在笔试、面试中的成绩（百分制）如下图所示，你觉得谁应该被录取？
（笔试和面试的成绩分别按 60% 和 40% 计入总分）
解：根据题意，求甲、乙成绩的加权平均数，得
答：因为_____＞_____，所以_____将被录取.
小青在七年级第二学期的数学成绩如下表格，请按图示的平时、期中、期末的权重，计算小青同学该学期总评成绩.
先计算小青的平时成绩：
(89 + 78 + 85)÷3
再计算小青的总评成绩：
84×10% + 90×30% + 87×60%
例2 某跳水队为了解运动员的年龄情况，作了一次年龄调查，结果如下：13 岁 8 人，14 岁 16 人，15 岁 24 人，16 岁 2 人. 求这个跳水队运动员的平均年龄(结果取整数).
解：这个跳水队运动员的平均年龄为：　
≈_____（岁）. 答：这个跳水队运动员的平均年龄约为_____.
8 + 16 + 24 + 2
某校八年级一班有学生 50 人，八年级二班有学生 45 人，期末数学测试中，一班学生的平均分为 81.5 分，二班学生的平均分为 83.4 分，这两个班 95 名学生的平均分是多少？
解： (81.5×50 + 83.4×45)÷95 = 7828÷95 = 82.4（分）.答：这两个班 95 名学生的平均分是 82.4 分.
1. 一组数据为 10，8，9，12，13，10，8，则这组数据的平均数是_____.
3. 某公司有 15 名员工，他们所在的部门及相应每人所创的年利润（万元）如下表：
该公司每人所创年利润的平均数是_____万元.
4. 某纺织厂订购了一批棉花，棉花纤维长短不一，主要有 3 cm，5 cm，6 cm 三种长度．随意地取出 10 g 棉花并测出三种长度的棉花纤维含量，得到下面的结果：
问：这批棉花的平均纤维长度是多少？
解：这批棉花的平均纤维长度为：
分析：在取出的 10 g 棉花中，纤维长度为 3 cm，5 cm，6 cm 的棉花各占 0.25，0.4，0.35，显然含量多的棉花纤维的长度对平均长度的影响大，所以要用加权平均数的方法来求出这批棉花纤维的平均长度.
5. 某次歌唱比赛，两名选手的成绩如下：（1）若按三项平均数取第一名，则_______是第一名.
所以，此时第一名是选手 A.
（2）若三项测试得分按 3 : 6 : 1 的比例确定个人的测试成绩，此时第一名是谁？