




湘教版数学七年级下册 4.1.2 相交直线所成的角 课件
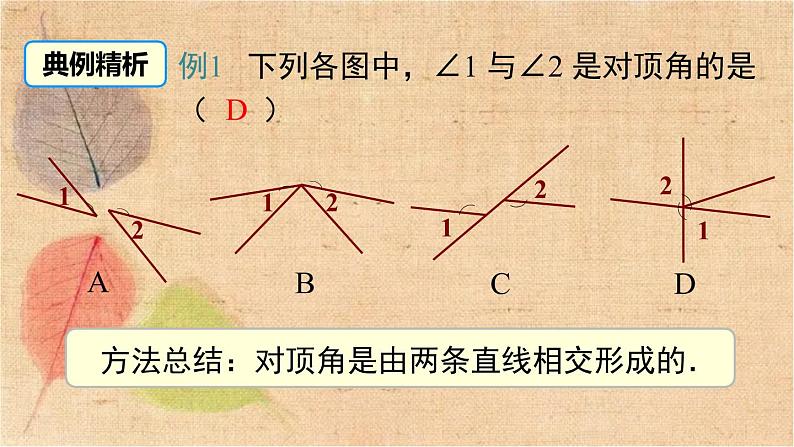
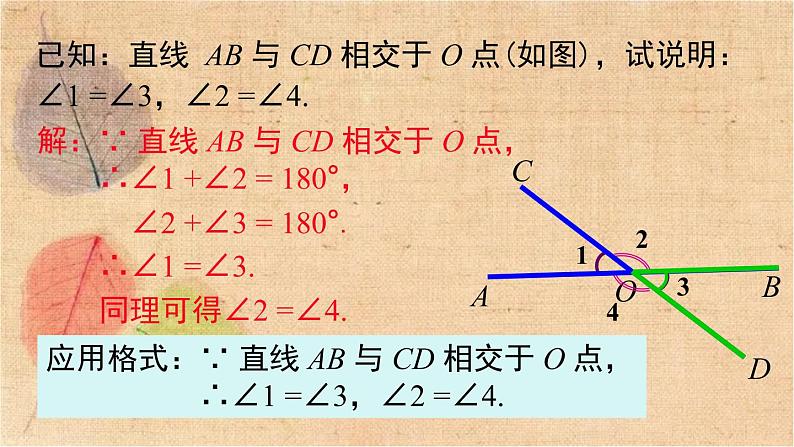
展开4.1 平面上两条直线的位置关系第4章 相交线与平行线4.1.2 相交直线所成的角直线与直线相交于一点,并形成了四个角.你发现了什么?图片引入活动:握紧把手时,随着两个把手之间的角逐渐变小,剪刀刃之间的角也相应变小直到剪开布片.如果把剪刀的构造看作两条相交的直线,这就关系到两条相交直线所成的角的问题.对顶角的概念1234ABCDO对顶角:两个角有公共顶点,并且一个角的两边分别是另一个角两边的 ,这样的两个角叫做对顶角. 图中∠1 的对顶角是______.反向延长线∠3概念学习例1 下列各图中,∠1 与∠2 是对顶角的是( )D方法总结:对顶角是由两条直线相交形成的.典例精析猜想:对顶角相等.问题:对顶角∠1 与∠3 在数量上又有什么关系呢?对顶角的性质思考:你能利用有关知识来推导∠1 与∠3 的数量关系吗? 我们已经知道平角为 180°,因而∠1 与∠2,∠2 与∠3,∠3 与∠4,∠4 与∠1 的和均为 180°.OABCD已知:直线 AB 与 CD 相交于 O 点(如图),试说明:∠1 =∠3,∠2 =∠4.解:∵ 直线 AB 与 CD 相交于 O 点,∴∠1 +∠2 = 180°, ∠2 +∠3 = 180°.∴∠1 =∠3.同理可得∠2 =∠4.应用格式:∵ 直线 AB 与 CD 相交于 O 点, ∴∠1 =∠3,∠2 =∠4.想一想:图中是对顶角量角器,你能说出用它测量角的原理吗?对顶角相等∠2 = 180°-∠1 = 140°.例2 如图,直线 a,b 相交,∠1 = 40°,求∠2,∠3,∠4 的度数.∵ 直线 a 与 b 相交于一点,∠1 = 40°, ∴∠3 =∠1 = 40°,解:∴∠4 =∠2 = 140°. 掌握对顶角的性质是解题的关键!3. 若 1:2 = 2:7,则∠1,∠2,∠3,∠4 各角的度数分别为_____________________.2. 若∠2 是 ∠1 的 3 倍,则∠1,∠2,∠3,∠4 各个角的度数分别为_____________________.1. 若 ∠1 +∠3 = 60°,则∠1,∠2,∠3,∠4 各角的度数分别为_____________________.30°,150°,30°,150°45°,135°,45°,135°40°,140°,40°,140°变式训练:例3 如图,直线 AB、CD,EF 相交于点 O,∠1=40°,∠BOC=110°,求∠2 的度数.解:因为∠1=40°, ∠BOC=110° (已知), 所以∠BOF=∠BOC -∠1 =110°-40°=70°. 因为∠BOF=∠2 (对顶角相等), 所以∠2=70° (等量代换).注意:隐含条件“对顶角相等”.1. 如图,直线 AB、CD、EF 相交,若∠1 +∠5 = 180°,找出图中与∠1 相等的角.解:∠1 =∠3 (对顶角相等).因为∠5 +∠8 = 180°,且∠1 +∠5 = 180°,所以∠8 =∠1. 因为∠8 =∠6 (对顶角相等),所以∠6 =∠1.变式训练:综上可知,与∠1 相等的角有∠3,∠8,∠6.2. 如图,直线 AB、CD、EF、MN 相交,若∠2 =∠5,找出图中与∠2 互补的角.解:因为∠1 +∠2 = 180°, ∠2 +∠3 = 180°,所以∠2 的补角有∠1 和∠3.因为∠5 +∠6 = 180°,∠5 +∠8 = 180° 且∠2 =∠5,所以∠2 的补角有∠6 和∠8.所以图中与∠2 互补的角有∠1,∠3,∠6 和∠8.简称“三线八角” 如图,若再添加一条直线,即直线 EF 分别与两条直线 AB 和 CD 相交,构成了几个角?有什么特点?交流与合作同位角、内错角、同旁内角F活动1 观察∠1 与∠5 的位置关系:① 在直线 EF 的同旁(右边)② 在直线 AB、CD 的同一侧(上方)ACBDE12345678∠2 和∠6;∠3 和∠7;∠4 和∠8.图中的同位角还有哪些?同位角一、同位角的概念例4 下列图形中,∠1和∠2 是同位角的有( )AA. (1),(2) B. (3),(4) C. (1),(2),(3) D. (2),(3),(4)图形特征:在形如字母“F”的图形中有同位角.变式图形:图中的 ∠1 与∠2 都是同位角.归纳总结ACBDEF12345678活动2 观察∠3与∠5的位置关系:① 在直线 EF 的两侧② 在直线 AB、CD 之间∠4 和∠6图中的内错角还有哪些?内错角二、内错角的概念B变式图形:图中的 ∠1 与∠2 都是内错角.图形特征:在形如“Z”的图形中有内错角.归纳总结ACBDEF12345678活动3 观察∠4 与∠5 的位置关系:① 在直线 EF 的同旁② 在直线 AB、CD 之间∠3 和∠6图中还有哪些同旁内角?同旁内角三、同旁内角的概念A变式图形:图中的 ∠1 与∠2 都是同旁内角.图形特征:在形如“U”的图形中有同旁内角. 归纳总结FZU截线:同侧被截线:同旁截线:同侧被截线:之间截线:两侧被截线:之间都在截线同侧都在被截线之间①必有三条直线;②这三类角都没有公共顶点;③都表示角之间的位置关系总结归纳例7 如图,直线 DE 截 AB ,AC,构成 8 个角,指出所有的同位角,内错角,同旁内角. 解:两条直线 AB,AC 被直线 DE 所截,所以 8 个角中,同位角有:∠1 与∠8,∠2 与∠5,∠3 与∠6,∠4 与∠7;内错角有:∠1 与∠6,∠4 与∠5;同旁内角有:∠1 与∠5,∠4 与∠6.典例精析变式:∠A 与∠8 是哪两条直线被哪条直线所截得的角?它们是什么关系的角?∠A 与∠5 呢?∠A 与∠4 呢?解:∠A 与∠8 是直线 AB,DE 被直线 AC 所截形成的内错角.∠A 与∠5 是直线 AB,DE 被直线 AC 所截形成的同旁内角.∠A 与∠4 是直线 AC,DE 被直线AB 所截形成的同位角.练一练:识别哪些角是同位角、内错角、同旁内角12(1)同位角12(2)12(3)12(4)12(5)12(6)12(7)12(8)1212(9)(10)同位角同位角同位角同位角内错角同旁内角例8 如图,直线 DE,BC 被直线 AB 所截. (1)∠1 和∠2, ∠1 和∠3,∠1 和∠4 各是什么位置关系的角?解:∠1 和∠2 是内错角,∠1 和∠3 同旁内角,∠1 和∠4 是同位角.温馨提示:解题之前要明确哪两条直线被哪条直线所截.解:如果∠1 =∠4,由对顶角相等,得∠2 =∠4,那么∠1 =∠2. 因为∠3 和∠4 互补,即∠4 +∠3 = 180°,又∠1 =∠4,所以∠1 +∠3 = 180°,即∠1 与∠3 互补.(2)如果∠1 =∠4,那么∠1 与∠2 相等吗?∠1 与∠3 互补吗?为什么?1. 下列各图中,∠1,∠2 是对顶角吗?()12()12()21不是是不是2. 如图,∠DAB 和∠ABC 的位置关系是( ) A. 同位角 B. 同旁内角 C. 内错角 D. 以上结论都不对3. 如图,∠1 和 ∠2 不能构成同位角的图形是( )CD 解:(1)∠AOC 的补角是∠AOD 和∠COB; ∠BOE 的补角是∠EOA 和∠BOF.4. 如图,直线 AB,CD,EF 相交于点 O. (1) 写出∠AOC,∠BOE 的补角; (2) 写出∠DOA,∠EOC 的对顶角; (3) 如果∠AOC = 50°,求∠BOD,∠COB 的度数.(2)∠DOA 的对顶角是∠COB; ∠EOC 的对顶角是∠DOF.(3)∠BOD =∠AOC = 50°, ∠COB = 180° -∠AOC = 130°.(2) 如图 2,若 ED,BC 被 AF 所截,则∠3 与____是内错角;(1) 如图 1,若 ED,BF 被 AB 所截,则∠1 与____是同位角; 5. 看图填空:∠2∠4图1图2(3) 如图 3,∠1 与∠3 是 AB 和 AF 被_____所截构成的 角;DE内错(4) 如图 4,∠2 与∠4 是 和 被 BC 所截构成的_____角.ABAF同位图3图46. 如图,直线 AB,CD 相交于点 O,∠EOC = 70°, OA 平分∠EOC ,求∠BOD 的度数.ABCDEO7. 根据地图显示填空:学校与游乐场所在的角形成一对( )角;学校与超市所在的角形成一对( )角;学校与飞机场所在的角形成一对( )角.同位同旁内内错拓展题:观察下列各图,寻找对顶角 (不含平角) .(1) 如图 1,图中共有 对对顶角;(2) 如图 2,图中共有 对对顶角;(3) 如图 3,图中共有 对对顶角;(4) 研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有 n 条直线相交于一点,则可形成 对对顶角;(5) 若有 10 条直线相交于一点,则可形成 对对顶角.图1图2图32612n(n-1)90视频:寻找对顶角点击视频开始播放生活中的数学:三线八角手势记忆法同位角内错角同旁内角视频:三线八角微课点击视频开始播放相交线所成的角对顶角对顶角相等三线八角同位角、内错角、同旁内角





