数学（北京卷）-学易金卷：2023年中考第一次模拟考试卷

这是一份数学（北京卷）-学易金卷：2023年中考第一次模拟考试卷，文件包含北京卷全解全析2023年中考数学第一模拟考试卷docx、北京卷参考答案2023年中考数学第一模拟考试卷docx、北京卷考试版A42023年中考数学第一模拟考试卷docx、北京卷考试版A32023年中考数学第一模拟考试卷docx等4份试卷配套教学资源，其中试卷共54页， 欢迎下载使用。

（考试时间：120分钟 试卷满分：100分）
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2．回答第Ⅰ卷时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。写在本试卷上无效。
3．回答第Ⅱ卷时，将答案写在答题卡上。写在本试卷上无效。
4．考试结束后，将本试卷和答题卡一并交回。
第Ⅰ卷
一、选择题（共16分，每题2分）第1-8题均有四个选项，符合题意的选项只有一个．
1．下列几何体中，是圆柱的为（ ）
A．B．C．D．
2．卢塞尔体育场是卡塔尔世界杯的主体育场，由中国建造，是卡塔尔规模最大的体育场．世界杯之后，将有约170000个座位将捐赠给需要体育基础设施的国家，其中大部分来自世界杯决赛场地卢塞尔体育场，170000这个数用科学记数法表示为（ ）
A．0.17×105B．1.7×105C．17×104D．1.7×106
3．如图，在数轴上表示实数的点可能是（ ）
A．点PB．点QC．点MD．点N
4．如图，直线a，b相交，∠1＝150°，则∠2+∠3＝（ ）
A．150°B．120°C．60°D．30°
5．一个布袋内只装有2个黑球和1个白球，这些球除颜色外其余都相同，随机摸出一个球后再随机摸出一个球，则两次摸出的球都是黑球的概率是（ ）
A．B．C．D．
6．不解方程，判断下列方程中有实数根的是（ ）
A．2x2+4x+3＝0B．x2﹣2x+3＝0C．2x2+5＝0D．x2+x＝0
7．研究与试验发展（R&D）经费是指报告期为实施研究与试验发展（R&D）活动而实际发生的全部经费支出．基础研究活动是研究与试验发展（R&D）活动的重要组成．下面的统计图是自2016年以来全国基础研究经费及占R&D经费比重情况．
根据统计图提供的信息，下面四个推断中错误的是（ ）
A．2016年至2021年，全国基础研究经费逐年上升
B．2016年至2021年，全国基础研究经费占R&D经费比重逐年上升
C．2016年至2021年，全国基础研究经费平均值超过1000亿元
D．2021年全国基础研究经费比2016年的2倍还多
8．将一圆柱形小水杯固定在大圆柱形容器底面中央，小水杯中有部分水，现用一个注水管沿大容器内壁匀速注水，如图所示，则小水杯水面的高度h（cm）与注水时间t（min）的函数图象大致是（ ）
A．B．
C．D．
第Ⅱ卷
二、填空题（本大题共8小题，每小题2分，共16分）
9．若在实数范围内有意义，则实数x的取值范围是 ．
10．方程＝的解为 ．
11．因式分解mx2+2mx+m＝ ．
12．若（﹣1，y1），（﹣3，y2）在反比例函数y＝（k＞0）的图象上，则y1 y2.（选填：“＞”、“＜”或“＝”）
13．某校征集校运会会徽，遴选出甲、乙、丙三种图案．为了解何种图案更受欢迎，随机调查了该校100名学生，其中68名同学喜欢甲图案，若该校共有2000人，根据所学的统计知识可以估计该校喜欢甲图案的学生有 人．
14．如图，射线OC是∠AOB的平分线，P是射线OC上一点，PD⊥OA于点D，DP＝6，若E是射线OB上一点，OE＝4，则△OPE的面积是 ．
15．如图，在矩形ABCD中，AB＝4，BC＝5，E点为BC边延长线一点，且CE＝3．连接AE交边CD于点F，过点D作DH⊥AE于点H，则DH＝ ．
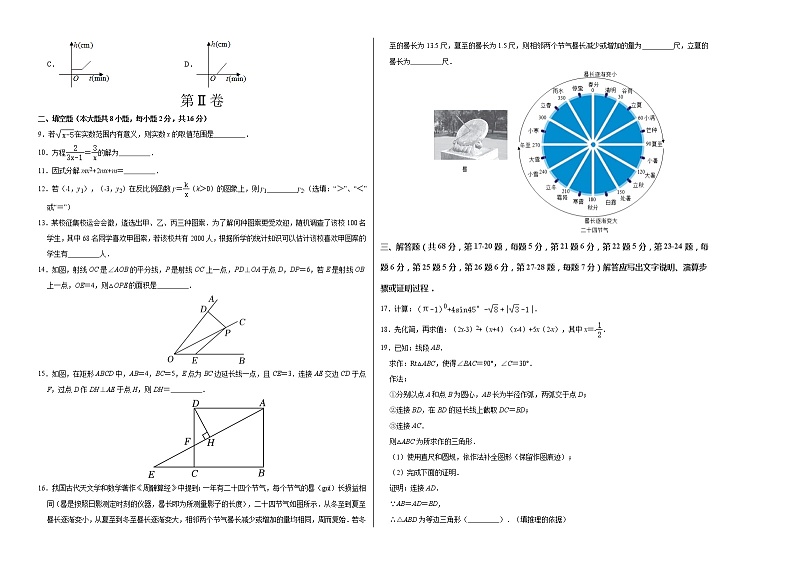
16．我国古代天文学和数学著作《周髀算经》中提到：一年有二十四个节气，每个节气的晷（guǐ）长损益相同（晷是按照日影测定时刻的仪器，晷长即为所测量影子的长度），二十四节气如图所示．从冬至到夏至晷长逐渐变小，从夏至到冬至晷长逐渐变大，相邻两个节气晷长减少或增加的量均相同，周而复始．若冬至的晷长为13.5尺，夏至的晷长为1.5尺，则相邻两个节气晷长减少或增加的量为 尺，立夏的晷长为 尺．
三、解答题（共68分，第17-20题，每题5分，第21题6分，第22题5分，第23-24题，每题6分，第25题5分，第26题6分，第27-28题，每题7分）解答应写出文字说明、演算步骤或证明过程．
17．计算：．
18．先化简，再求值：（2x﹣3）2+（x+4）（x﹣4）+5x（2﹣x），其中x＝﹣．
19．已知：线段AB．
求作：Rt△ABC，使得∠BAC＝90°，∠C＝30°．
作法：
①分别以点A和点B为圆心，AB长为半径作弧，两弧交于点D；
②连接BD，在BD的延长线上截取DC＝BD；
③连接AC．
则△ABC为所求作的三角形．
（1）使用直尺和圆规，依作法补全图形（保留作图痕迹）；
（2）完成下面的证明．
证明：连接AD．
∵AB＝AD＝BD，
∴△ABD为等边三角形（ ）．（填推理的依据）
∴∠B＝∠ADB＝60°．
∵CD＝BD，
∴AD＝CD
∴∠DAC＝ （ ）．（填推理的依据）
∴∠ADB＝∠C+∠DAC＝60°．
∴∠C＝30°．
在△ABC中，
∠BAC＝180°﹣（∠B+∠C）＝90°．
20．已知关于x的方程x2﹣2mx+m2﹣9＝0．
（1）求证：此方程有两个不相等的实数根；
（2）设此方程的两个根分别为x1，x2，若x1+x2＝6，求m的值．
21．如图，点A、F、C、D在同一直线上，点B和点E分别在直线AD的两侧，且AB＝DE，∠A＝∠D，AF＝DC．
（1）求证：四边形BCEF是平行四边形；
（2）若∠DEF＝90°，DE＝8，EF＝6，当AF为 时，四边形BCEF是菱形．
22．在平面直角坐标系xOy中，一次函数y＝kx+b（k≠0）的图象经过点A（0，﹣1），B（1，0）．
（1）求k，b的值；
（2）当x＞1时，对于x的每一个值，函数y＝﹣2x+n的值小于一次函数y＝kx+b的值，直接写出n的取值范围．
23．2022年是中国共产主义青年团建团100周年．某校举办了一次关于共青团知识的竞赛，七、八年级各有300名学生参加了本次活动，为了解两个年级的答题情况，从两个年级各随机抽取了20名学生的成绩进行调查分析．下面给出了部分信息：
a．七年级学生的成绩整理如下（单位：分）：
57 67 69 75 75 75 77 77 78 78 80 80 80 80 86 86 88 88 89 96
b．八年级学生成绩的频数分布直方图如图（数据分成四组：60≤x＜70，70≤x＜80，80≤x＜90，90≤x≤100）：
其中成绩在80≤x＜90的数据如下（单位：分）：
80 80 81 82 83 84 85 86 87 89
c．两组样本数据的平均数、中位数、众数如下表所示：
根据所给信息，解答下列问题：
（1）m＝ ，n＝ ；
（2）估计 年级学生的成绩高于平均分的人数更多；
（3）若成绩达到80分及以上为优秀，估计七年级和八年级此次测试成绩优秀的总人数．
24．如图，A是⊙O上一点，BC是⊙O的直径，BA的延长线与⊙O的切线CD相交于点D，E为CD的中点，AE的延长线与BC的延长线交于点P．
（1）求证：AP是⊙O的切线；
（2）若OC＝CP，AB＝，求CD的长．
25．跳台滑雪是冬季奥运会的比赛项目之一．如图，运动员通过助滑道后在点A处起跳经空中飞行后落在着陆坡BC上的点P处，他在空中飞行的路线可以看作抛物线的一部分．这里OA表示起跳点A到地面OB的距离，OC表示着陆坡BC的高度，OB表示着陆坡底端B到点O的水平距离．建立如图所示的平面直角坐标系，从起跳到着陆的过程中，运动员的竖直高度y（单位：m）与水平距离x（单位：m）近似满足函数关系y＝﹣+bx+c．已知OA＝70m，OC＝60m，落点P的水平距离是40m，竖直高度是30m．
（1）点A的坐标是 ，点P的坐标是 ；
（2）求满足的函数关系y＝﹣+bx+c；
（3）运动员在空中飞行过程中，当他与着陆坡BC竖直方向上的距离达到最大时，直接写出此时的水平距离．
26．在平面直角坐标系xOy中，点A（x1，y1）、点B（x2，y2）为抛物线y＝ax2﹣2ax+a（a≠0）上的两点．
（1）求抛物线的对称轴；
（2）当﹣2＜x1＜﹣1且1＜x2＜2时，试判断y1与y2的大小关系并说明理由；
（3）若当t＜x1＜t+1且t+2＜x2＜t+3时，存在y1＝y2，求t的取值范围．
27．已知：如图，OB＝BA，∠OBA＝150°，线段BA绕点A逆时针旋转90°得到线段AC．连接BC，OA，OC，过点O作OD⊥AC于点D．
（1）依题意补全图形；
（2）求∠DOC的度数．
28．在平面直角坐标系xOy中，点P不在坐标轴上，点P关于x轴的对称点为P1，点P关于y轴的对称点为P2，称△P1PP2为点P的“关联三角形”．
（1）已知点A（1，2），求点A的“关联三角形”的面积；
（2）如图，已知点B（m，m），⊙T的圆心为T（2，2），半径为2．若点B的“关联三角形”与⊙T有公共点，直接写出m的取值范围；
（3）已知⊙O的半径为r，OP＝2r，若点P的“关联三角形”与⊙O有四个公共点，直接写出∠PP1P2的取值范围．
年级
平均数
中位数
众数
七年级
79.05
79
m
八年级
79.2
n
74