






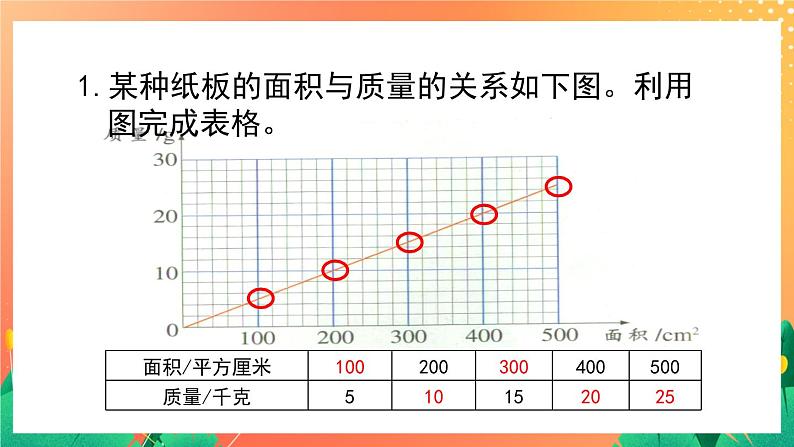
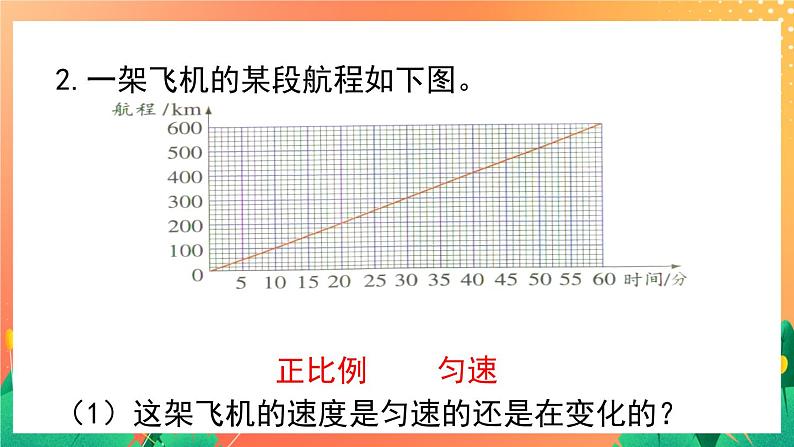
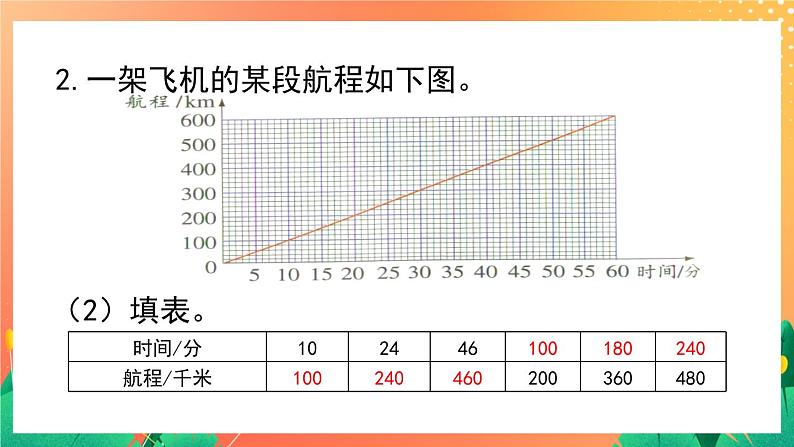
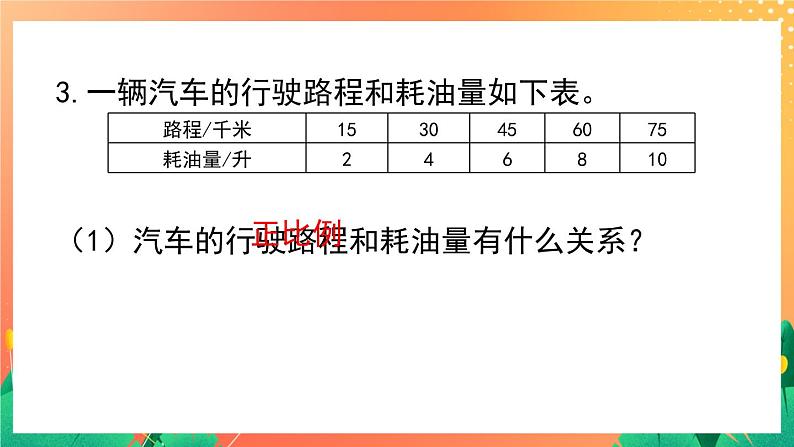

- 1.2《正比例(一)》课件+教案+练习ppt 课件 2 次下载
- 1.3《解比例》 课件+教案+练习ppt 课件 1 次下载
- 1.5《正比例应用问题 》(2课时)课件+教案+练习ppt 课件 1 次下载
- 1.6《反比例(一)》课件+教案+练习ppt 课件 1 次下载
- 1.7《反比例(二)》课件+教案 课件 1 次下载
1.4《正比例(二)》课件+教案+练习ppt
展开正比例(二)
【教学目标】
1.使学生初步理解正比例的意义和性质,能够正确判断成正比例的量。
2.培养学生仔细审题,认真思考,探索规律的良好习惯。
【教学重难点】
理解正比例的意义和性质。
【教学过程】
一、复习引入:
我们已学了一些常见的数量关系,谁能来说一说:
1.路程、速度、时间;
2.单价、数量、总量;
3.工作效率、工作时间、工作总量;
……
二、先观察、后概括:
1.例1:一列火车行驶的时间和路如下表:
时间(小时) | 1 | 2 | 3 | 4 | 5 | 6 | …… |
路程(千米) | 90 | 180 | 270 | 360 | 450 | 540 | …… |
观察上表,回答下列问题:
(1)表中有哪两个量是相关联的?
(2)路程是怎样随着行车时间的变化而变化的?
(3)相对应的路程和时间的比值分别是多少?表示什么意思?
小结:从上表可以看出,时间和路程是两种相关联的量,路程是随着时间的变化而变化的,时间扩大,路程随着扩大;时间缩小,路程随着缩小。相对应的路程和时间的比的比值是相等的(或一定的),这个比表示速度。
写成关系式是:=速度(一定)
2.新改例2:在一间布店的柜台上,有一张写着某种花布的米数和总价的表:
由上表可以发现:
(1)表中有哪两个量是相关联的?
(2)总价是怎样随着数量的变化而变化的?
(3)相对应的总价和数量的比值分别是多少?表示什么意思?
小结:从上表可以看出,总价和数量是两种相关联的量,总价是随着数量的变化而变化的,数量扩大,总价随着扩大;数量缩小,总价随着缩小。相对应的总价和数量的比的比值是相等的(或一定的),这个比表示布的单价。
写成关系式是:=单价(一定)
思考:比较例1.例2,它们有什么共同点?
概括:
(1)两种相关联的量,其中一种量变化,另一种量也随着变化。
(2)如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,他们的关系叫做正比例关系。如果用字母X、Y表示两种相关联的量,用K表示比值(一定),则数量关系可以概括下面的式子:
= K(一定)
(结合例1.例2说一说)
三、练一练
(1)某市造纸厂的生产情况如下表,根据表回答问题。
问:
A.表中有哪两种量?它们是不是相关联的量?
(表中有时间和生产量两种量。它们是相关联的量)
B.写出几组这两种量中相对应的两个数的比,求出比值,并比较比值的大小。(比值相等)
C.说明这个比值所表示的意义(每天生产的吨数(或生产效率))
D.表中相关联的两种量成正比例关系吗?为什么?
(2)每袋面粉的重量一定,面粉的总重量和袋数是不是成正比例?
小结:面粉的总重量和袋数是两种相关联的量,总重量/袋数=每袋面粉的重量(一定),所以面粉的总重量和袋数成正比例。
(3)判断下面每题中的两种量是不是成正比例,并说明理由。
A.苹果的单价一定,购买苹果的数量和总价。
B.学生跳高的高度和他们的身高
C.某班总人数一定,男生人数和女生人数
D.圆柱的底面周长和侧面积
E.圆的直径和周长
F.正方形的周长和边长
四、小结:
1.什么叫是正比例关系?用式子怎样表示?
2.怎样判断两种量是否成正比例关系?
【板书设计】
正比例
表达式:y/x=k(一定)
判断依据:两个相关的两,比值一定










