高中数学高考第05讲 函数的奇偶性与周期性（讲）原卷版

第05讲  函数的奇偶性与周期性

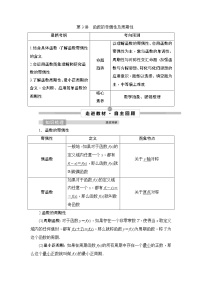
【学科素养】数学抽象、数学运算、数学建模、逻辑推理、直观想象

【课标解读】

    1.抽象函数的奇偶性与周期性；

2.利用奇偶性与周期性求参数取值范围；

3.函数性质的综合应用问题.

【备考策略】

1.判断函数的奇偶性与周期性；

2.函数的奇偶性、周期性，通常与抽象函数、函数的图象以及函数的单调性结合考查，常结合三角函数加以考查．

【核心知识】

知识点一  函数的奇偶性

知识点二   函数的周期性

(1)周期函数：对于函数y＝f(x)，如果存在一个非零常数T，使得当x取定义域内的任何值时，都有f(x＋T)＝f(x)，那么就称函数y＝f(x)为周期函数，称T为这个函数的周期.

(2)最小正周期：如果在周期函数f(x)的所有周期中存在一个最小的正数，那么这个最小正数就叫做f(x)的最小正周期.

【特别提醒】

1.(1)如果一个奇函数f(x)在原点处有定义，即f(0)有意义，那么一定有f(0)＝0.

(2)如果函数f(x)是偶函数，那么f(x)＝f(|x|).

2.奇函数在两个对称的区间上具有相同的单调性；偶函数在两个对称的区间上具有相反的单调性.

3.函数周期性常用结论

对f(x)定义域内任一自变量的值x：

(1)若f(x＋a)＝－f(x)，则T＝2a(a>0).

(2)若f(x＋a)＝，则T＝2a(a>0).

(3)若f(x＋a)＝－，则T＝2a(a>0).

4.对称性的三个常用结论

(1)若函数y＝f(x＋a)是偶函数，则函数y＝f(x)的图象关于直线x＝a对称.

(2)若对于R上的任意x都有f(2a－x)＝f(x)或f(－x)＝f(2a＋x)，则y＝f(x)的图象关于直线x＝a对称.

(3)若函数y＝f(x＋b)是奇函数，则函数y＝f(x)的图象关于点(b，0)中心对称.

【高频考点】

高频考点一   函数奇偶性的判定

例1．【2020·全国Ⅱ卷】设函数，则f(x)

A．是偶函数，且在单调递增   B．是奇函数，且在单调递减

C．是偶函数，且在单调递增 D．是奇函数，且在单调递减

【方法技巧】判断函数奇偶性的常用方法

(1)定义法：

确定函数的奇偶性时，必须先判定函数定义域是否关于原点对称．若对称，再化简解析式后验证f(－x)＝±f(x)或其等价形式f(－x)±f(x)＝0是否成立．

(2)图象法：

f(x)的图像关于原点对称，f(x)为奇函数；

f(x)的图像关于y轴对称，f(x)为偶函数。

(3)性质法：

设f(x)，g(x)的定义域分别是D1，D2，那么在它们的公共定义域上：奇＋奇＝奇，奇×奇＝偶，偶＋偶＝偶，偶×偶＝偶，奇×偶＝奇．

【举一反三】(2021·湖北省丹江口市一中模拟)设f(x)＝ex＋e－x，g(x)＝ex－e－x，f(x)，g(x)的定义域均为R，下列结论错误的是(　　)

A．|g(x)|是偶函数　　　　   B．f(x)g(x)是奇函数

C．f(x)|g(x)|是偶函数   D．f(x)＋g(x)是奇函数

【变式探究】【2020年高考浙江】函数y=xcos x+sin x在区间[–π，π]上的图象可能是

高频考点二   函数奇偶性的应用

例2．【2020·江苏卷】已知y=f(x)是奇函数，当x≥0时，，则的值是       ．

【方法技巧】与函数奇偶性有关的问题及解题策略

(1)求函数的值：利用奇偶性将待求值转化为已知区间上的函数值求解．

(2)求函数解析式：先将待求区间上的自变量转化到已知区间上，再利用奇偶性求出，或充分利用奇偶性构造关于f(x)的方程(组)，从而得到f(x)的解析式．

(3)求解析式中的参数值：在定义域关于原点对称的前提下，利用f(x)为奇函数⇔f(－x)＝－f(x)，f(x)为偶函数⇔f(x)＝f(－x)，列式求解，也可利用特殊值法求解．对于在x＝0处有定义的奇函数f(x)，可考虑列等式f(0)＝0求解．

【举一反三】(2019·全国卷Ⅱ)设f (x)为奇函数，且当x≥0时，f (x)＝ex－1，则当x<0时，f (x)＝(　　)

A．e－x－1  B．e－x＋1  C．－e－x－1  D．－e－x＋1

【变式探究】(2019·全国卷Ⅱ)已知f(x)是奇函数，且当x＜0时，f(x)＝－eax.若f(ln 2)＝8，则a＝________.

高频考点三  函数的周期性

例3. (2018·全国Ⅱ卷)已知f(x)是定义域为(－∞，＋∞)的奇函数，满足f(1－x)＝f(1＋x).若f(1)＝2，则f(1)＋f(2)＋f(3)＋…＋f(50)＝(　　)

A.－50   B.0   C.2   D.50

【方法技巧】

(1)求解与函数的周期性有关的问题，应根据题目特征及周期定义，求出函数的周期．

(2)周期函数的图象具有周期性，如果发现一个函数的图象具有两个对称性(注意：对称中心在平行于x轴的直线上，对称轴平行于y轴)，那么这个函数一定具有周期性．

【变式探究】(2021·广东省韶关市一中模拟)已知函数f (x)的图象关于原点对称，且周期为4，若f (－1)＝2，则f (2 021)＝(　　)

A．2  B．0  C．－2  D．－4

高频考点四   函数性质的综合应用

例4. (2021·河北模拟)定义在R上的偶函数f (x)满足f (x＋2)＝f (x)，且在[－1,0]上单调递减．设a＝f (－2.8)，b＝f (－1.6)，c＝f (0.5)，则a，b，c的大小关系是(　　)

A．a>b>c B．c>a>b

C．b>c>a D．a>c>b

【举一反三】(2021·海南省三亚市一中模拟)定义在R上的偶函数f (x)满足f (x＋3)＝f (x)．若f (2)>1，f (7)＝a，则实数a的取值范围为(　　)

A．(－∞，－3) B．(3，＋∞)

C．(－∞，－1) D．(1，＋∞)

【方法技巧】函数性质综合应用问题的常见类型及解题策略

(1)函数单调性与奇偶性的综合．注意函数单调性及奇偶性的定义，以及奇、偶函数图象的对称性。

(2)周期性与奇偶性的综合．此类问题多考查求值问题，常利用奇偶性及周期性进行变换，将所求函数值的自变量转化到已知解析式的函数定义域内求解。

(3)单调性、奇偶性与周期性的综合．解决此类问题通常先利用周期性转化自变量所在的区间，然后利用奇偶性和单调性求解。

（4）应用奇函数图象关于原点对称，偶函数图象关于y轴对称。

【变式探究】(2021·陕西省延安中学模拟)在R上定义的函数f(x)是偶函数，且f(x)＝f(2－x)．若f(x)在区间[1，2]上是减函数，则f(x)(　　)

A．在区间[－2，－1]上是增函数，在区间[3，4]上是增函数

B．在区间[－2，－1]上是增函数，在区间[3，4]上是减函数

C．在区间[－2，－1]上是减函数，在区间[3，4]上是增函数

D．在区间[－2，－1]上是减函数，在区间[3，4]上是减函数