






高中数学高考49第九章 平面解析几何 9 1 直线的方程课件PPT
展开NEIRONGSUOYIN
基础知识 自主学习
题型分类 深度剖析
1.直线的倾斜角(1)定义:当直线l与x轴相交时,取x轴作为基准,x轴正向与直线l__________之间所成的角叫做直线l的倾斜角.当直线l与x轴____________时,规定它的倾斜角为0°.(2)范围:直线l倾斜角的范围是___________.
ZHISHISHULI
2.斜率公式(1)若直线l的倾斜角α≠90°,则斜率k=_____.(2)P1(x1,y1),P2(x2,y2)在直线l上且x1≠x2,则l的斜率k=______.
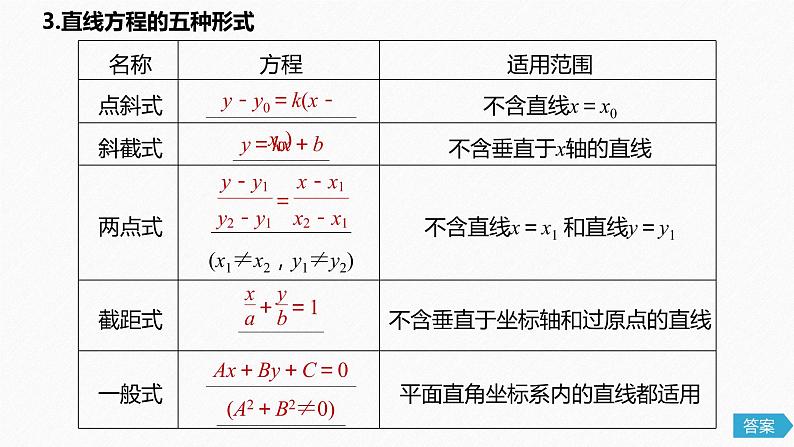
3.直线方程的五种形式
Ax+By+C=0(A2+B2≠0)
y-y0=k(x-x0)
1.直线都有倾斜角,是不是都有斜率?倾斜角越大,斜率k就越大吗?
2.“截距”与“距离”有何区别?当截距相等时应注意什么?
提示 “截距”是直线与坐标轴交点的坐标值,它可正,可负,也可以是零,而“距离”是一个非负数.应注意过原点的特殊情况是否满足题意.
1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)根据直线的倾斜角的大小不能确定直线的位置.( )(2)若直线的斜率为tan α,则其倾斜角为α.( )(3)斜率相等的两直线的倾斜角不一定相等.( )(4)经过任意两个不同的点P1(x1,y1),P2(x2,y2)的直线都可以用方程(y-y1)(x2-x1)=(x-x1)(y2-y1)表示.( )
2.[P86T3]若过点M(-2,m),N(m,4)的直线的斜率等于1,则m的值为A.1 B.4 C.1或3 D.1或4
3.[P100A组T9]过点P(2,3)且在两坐标轴上截距相等的直线方程为______________________.
解析 当截距为0时,直线方程为3x-2y=0;
4.(2018·石家庄模拟)直线x+(a2+1)y+1=0的倾斜角的取值范围是
5.如果A·C<0且B·C<0,那么直线Ax+By+C=0不通过A.第一象限 B.第二象限C.第三象限 D.第四象限
6.过直线l:y=x上的点P(2,2)作直线m,若直线l,m与x轴围成的三角形的面积为2,则直线m的方程为 .
解析 ①若直线m的斜率不存在,则直线m的方程为x=2,直线m,直线l和x轴围成的三角形的面积为2,符合题意;
x-2y+2=0或x=2
②若直线m的斜率k=0,则直线m与x轴没有交点,不符合题意;
综上可知,直线m的方程为x-2y+2=0或x=2.
题型一 直线的倾斜角与斜率
解析 直线2xcs α-y-3=0的斜率k=2cs α,
(2)直线l过点P(1,0),且与以A(2,1),B(0, )为端点的线段有公共点,则直线l斜率的取值范围为 .
1.若将本例(2)中P(1,0)改为P(-1,0),其他条件不变,求直线l斜率的取值范围.
2.若将本例(2)中的B点坐标改为(2,-1),其他条件不变,求直线l倾斜角的取值范围.
解 如图,直线PA的倾斜角为45°,
直线PB的倾斜角为135°,由图象知l的倾斜角的范围为[0°,45°]∪[135°,180°).
(1)倾斜角α与斜率k的关系
(2)斜率的两种求法①定义法:若已知直线的倾斜角α或α的某种三角函数值,一般根据k=tan α求斜率.
(3)倾斜角α范围与直线斜率范围互求时,要充分利用y=tan α的单调性.
跟踪训练1 (1)若平面内三点A(1,-a),B(2,a2),C(3,a3)共线,则a等于
解析 ∵平面内三点A(1,-a),B(2,a2),C(3,a3)共线,∴kAB=kAC,
(2)直线l经过A(3,1),B(2,-m2)(m∈R)两点,则直线l的倾斜角α的取值范围是 .
所以k=tan α≥1.
例2 求适合下列条件的直线方程:(1)经过点P(3,2),且在两坐标轴上的截距相等;
解 方法一 设直线l在x,y轴上的截距均为a,若a=0,即l过点(0,0)和(3,2),
∴a=5,∴l的方程为x+y-5=0,综上可知,直线l的方程为2x-3y=0或x+y-5=0.
方法二 由题意,所求直线的斜率k存在且k≠0,设直线方程为y-2=k(x-3),
即x+y-5=0或2x-3y=0.
解 设所求直线的斜率为k,依题意
又直线经过点A(-1,-3),
即3x+4y+15=0.
(3)过点A(1,-1)与已知直线l1:2x+y-6=0相交于B点且|AB|=5.
解 过点A(1,-1)与y轴平行的直线为x=1.
求得B点坐标为(1,4),此时|AB|=5,即x=1为所求.设过A(1,-1)且与y轴不平行的直线为y+1=k(x-1),
(k≠-2,否则与已知直线平行).
即3x+4y+1=0.综上可知,所求直线的方程为x=1或3x+4y+1=0.
在求直线方程时,应先选择适当的直线方程的形式,并注意各种形式的适用条件.若采用截距式,应注意分类讨论,判断截距是否为零;若采用点斜式,应先考虑斜率不存在的情况.
跟踪训练2 求适合下列条件的直线方程:(1)过点P(2,3),并且在两坐标轴上的截距互为相反数;
将P(2,3)代入方程,得a=-1,所以直线l的方程为x-y+1=0.综上,所求直线l的方程为3x-2y=0或x-y+1=0.
(2)过点A(-1,-3),倾斜角等于直线y=3x的倾斜角的2倍;
解 设直线y=3x的倾斜角为α,则所求直线的倾斜角为2α.
(3)直线过点(-3,4),且在两坐标轴上的截距之和为12.
解得a=-4或a=9.故所求直线方程为4x-y+16=0或x+3y-9=0.
题型三 直线方程的综合应用
命题点1 与基本不等式相结合求最值问题
例3 (2018·济南模拟)已知直线l过点M(2,1),且与x轴、y轴的正半轴分别相交于A,B两点,O为坐标原点,求当 取得最小值时直线l的方程.
解 设A(a,0),B(0,b),则a>0,b>0,
=2(a-2)+b-1=2a+b-5
当且仅当a=b=3时取等号,此时直线l的方程为x+y-3=0.
命题点2 由直线方程解决参数问题
例4 已知直线l1:ax-2y=2a-4,l2:2x+a2y=2a2+4,当0
跟踪训练3 过点P(4,1)作直线l分别交x轴,y轴正半轴于A,B两点,O为坐标原点.(1)当△AOB面积最小时,求直线l的方程;
因为直线l经过点P(4,1),
所以ab≥16,当且仅当a=8,b=2时等号成立,
(2)当|OA|+|OB|取最小值时,求直线l的方程.
1.直线 x-y+a=0(a为常数)的倾斜角为A.30° B.60° C.150° D.120°
解析 设直线的倾斜角为α,斜率为k,
∵0°≤α<180°,∴α=60°.
2.(2018·海淀模拟)过点(2,1)且倾斜角比直线y=-x-1的倾斜角小 的直线方程是A.x=2 B.y=1 C.x=1 D.y=2
解析 ∵直线y=-x-1的斜率为-1,
∴斜率不存在,∴过点(2,1)的直线方程为x=2.
3.已知过定点P(2,0)的直线l与曲线y= 相交于A,B两点,O为坐标原点,当△AOB的面积取到最大值时,直线l的倾斜角为A.150° B.135° C.120° D.不存在
显然直线l的斜率存在,设过点P(2,0)的直线l为y=k(x-2),
故直线l的倾斜角为150°.
4.如图中的直线l1,l2,l3的斜率分别为k1,k2,k3,则 A.k1
解析 设M的坐标为(a,b),若点M在直线y=x+1上,则有b=a+1. ①
联立①②可得a=4,b=5,即M的坐标为(4,5).故选B.
6.已知两点M(2,-3),N(-3,-2),直线l过点P(1,1)且与线段MN相交,则直线l的斜率k的取值范围是
∴要使直线l与线段MN相交,当l的倾斜角小于90°时,k≥kPN;
7.(2018·焦作期中)过点A(3,-1)且在两坐标轴上截距相等的直线有A.1条 B.2条 C.3条 D.4条
解析 ①当所求的直线与两坐标轴的截距都不为0时,设该直线的方程为x+y=a,把(3,-1)代入所设的方程得a=2,则所求直线的方程为x+y=2,即x+y-2=0;②当所求的直线与两坐标轴的截距为0时,设该直线的方程为y=kx,
综上,所求直线的方程为x+y-2=0或x+3y=0,故选B.
二、填空题9.一条直线经过点A(2, ),并且它的倾斜角等于直线y= 的倾斜角的2倍,则这条直线的一般式方程是 .
10.直线kx+y+2=-k,当k变化时,所有的直线都过定点______________.
解析 kx+y+2=-k可化为y+2=-k(x+1),根据直线方程的点斜式可知,此类直线恒过定点(-1,-2).
11.已知三角形的三个顶点A(-5,0),B(3,-3),C(0,2),则BC边上中线所在的直线方程为 .
12.经过点A(4,2),且在x轴上的截距等于在y轴上的截距的3倍的直线l的方程的一般式为 .
解析 当截距为0时,设直线方程为y=kx,则4k=2,
x+3y-10=0或x-2y=0
综上,直线l的一般式方程为x+3y-10=0或x-2y=0.
13.设点A(-1,0),B(1,0),直线2x+y-b=0与线段AB相交,则b的取值范围是________.
解析 b为直线y=-2x+b在y轴上的截距,如图,当直线y=-2x+b过点A(-1,0)和点B(1,0)时,b分别取得最小值-2和最大值2.∴b的取值范围是[-2,2].
解析 ∵动直线l0:ax+by+c-3=0(a>0,c>0)恒过点P(1,m),∴a+bm+c-3=0.又Q(4,0)到动直线l0的最大距离为3,
当且仅当c=2a=2时取等号.
三、解答题15.过点P(3,0)作一条直线,使它夹在两直线l1:2x-y-2=0与l2:x+y+3=0之间的线段AB恰好被点P平分,求此直线的方程.
解 设点A(x,y)在l1上,点B(xB,yB)在l2上.
故所求的直线方程为y=8(x-3),即8x-y-24=0.
16.已知直线l:kx-y+1+2k=0(k∈R).(1)证明:直线l过定点;
证明 直线l的方程可化为y=k(x+2)+1,故无论k取何值,直线l总过定点(-2,1).
(2)若直线l不经过第四象限,求k的取值范围;
解 直线l的方程可化为y=kx+2k+1,则直线l在y轴上的截距为2k+1,
故k的取值范围是k≥0.
(3)若直线l交x轴负半轴于点A,交y轴正半轴于点B,O为坐标原点,设△AOB的面积为S,求S的最小值及此时直线l的方程.
在y轴上的截距为1+2k,且k>0,
故S的最小值为4,此时直线l的方程为x-2y+4=0.
高中数学高考54第九章 平面解析几何 9 1 直线的方程课件PPT: 这是一份高中数学高考54第九章 平面解析几何 9 1 直线的方程课件PPT,共60页。PPT课件主要包含了内容索引,课时作业,基础知识自主学习,题型分类深度剖析,题型二求直线的方程等内容,欢迎下载使用。
高中数学高考51第九章 平面解析几何 9 3 圆的方程课件PPT: 这是一份高中数学高考51第九章 平面解析几何 9 3 圆的方程课件PPT,共60页。PPT课件主要包含了内容索引,课时作业,基础知识自主学习,题型分类深度剖析,题型一圆的方程等内容,欢迎下载使用。
高中数学高考62第九章 平面解析几何 9 8 曲线与方程课件PPT: 这是一份高中数学高考62第九章 平面解析几何 9 8 曲线与方程课件PPT,共60页。PPT课件主要包含了内容索引,课时作业,基础知识自主学习,题型分类深度剖析等内容,欢迎下载使用。












