初中数学湘教版八年级下册2.1 多边形课文内容课件ppt

这是一份初中数学湘教版八年级下册2.1 多边形课文内容课件ppt，共16页。PPT课件主要包含了知识引入，四边形，新知探究，什么是多边形，关于多边形的对角线，n-3，对角线，关于多边形的几个概念，多边形内角和，n-2等内容，欢迎下载使用。

在下列图案中你能发现哪些几何图形呢？
我们已经知道什么叫三角形。
你能根据三角形的定义，说出什么叫四边形吗？
由四条不在同一直线上的线段首尾顺次连结组成的平面图形，叫四边形。记为：四边形ABCD.
由三条不在同一直线上的线段首尾顺次连结组成的平面图形，叫三角形。
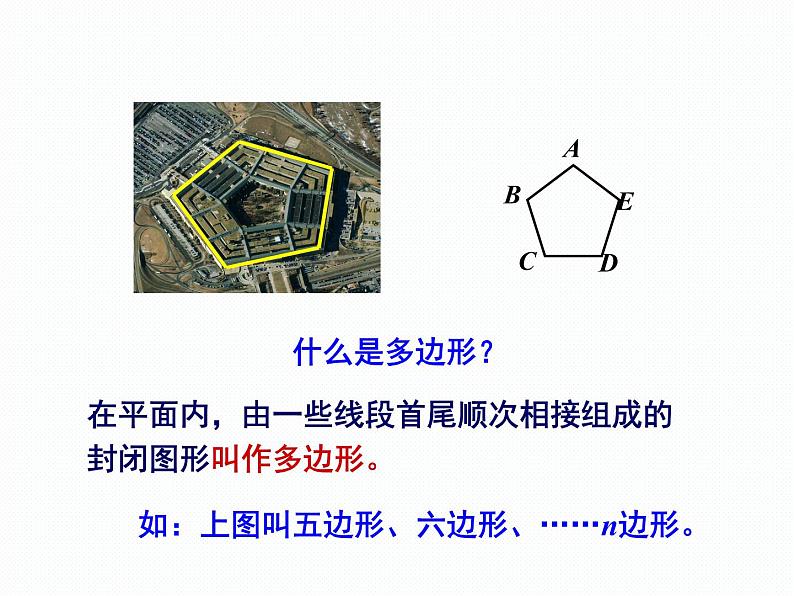
在平面内，由一些线段首尾顺次相接组成的封闭图形叫作多边形。
如：上图叫五边形、六边形、……n边形。
右图所示的图形也是多边形，但不在我们现在研究的范围内。
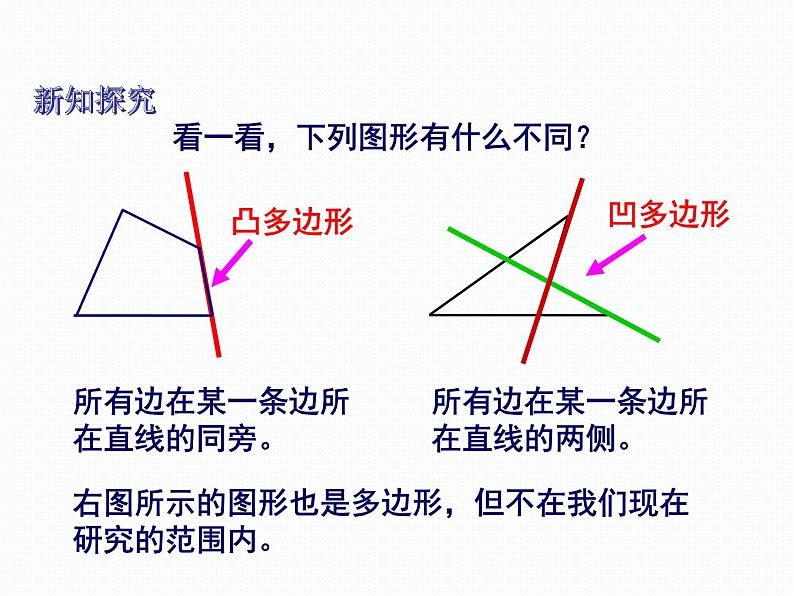
看一看，下列图形有什么不同？
所有边在某一条边所在直线的同旁。
所有边在某一条边所在直线的两侧。
从一个顶点出发，三角形能引出__条对角线;
五边形能引出__条对角线;
六边形能引出__条对角线;
n边形能引出 条对角线.
七边形能引出__条对角线;
四边形能引出__条对角线;
边：组成多边形的各条线段。
顶点：相邻两条边的公共端点
内角（角）：相邻两边组成的角
对角线：连接不相邻的两个顶点的线段
n边形有 条边， 角， 外角。
外角：一边和相邻一边的延长线所组成的角
一个多边形一共有多少条对角线？
关于特殊的多边形----正多边形
如果多边形各边都相等，各个角也都相等，那么这样的多边形就叫做正多边形.
如正三角形、正四边形（正方形）、正五边形等等 .
n边形的内角和等于(n-2) ·180°.
还有其他方法探究n边形的内角和公式吗？
如图，在n边形内任取一点O，与多边形各顶点连接，把n边形分成n个三角形，用n个三角形的内角和n·180°减去中心的周角360°，得n边形的内角和为（n-2）·180°.
这些不同方法的共性是什么？
作辅助线构造三角形，将多边形的内角和转化为三角形的内角和，这体现了化未知为已知的转化思想。
体现了多边形与三角形的关系。
例1、 (1)十边形的内角和是多少度？
解：(1)十边形的内角和是(10-2)×180°=1440°.
(2)一个多边形的内角和等于1980°，它是几边形？
解：设这个多边形的边数为n，则
例2、四边形ABCD的内角∠A∶∠B∶∠C∶∠D = 1∶2∶3∶4，求各个角的大小。
(n-2) ×180°=1980°, 解得 n=13.
所以这是一个十三边形.
解：∵ ∠A+∠B+∠C+∠D = 360°
例3、过某个多边形一个顶点的所有对角线，将这个多边形分成5个三角形。这个多边形是几边形？它的内角和是多少？
解：设多边形的边数为n，
它的内角和是：5×180°=900°
例4、已知一个多边形，它的内角和 等于五边形的内角和的2倍，求这个多边形的边数．
解：设边数为n，则可列方程为：
(n-2)×180°=(5-2)×180°×2
例5、已知一个多边形各个内角都相等，都等于150°，求这个多边形的边数.
解：设这个多边形的边数为n，
可得方程：(n-2)×180°=150×n
例6、一个多边形去掉一个内角后，其余各内角之和为2210°，求这个多边形的边数．
2210°＜(n-2) ×180°＜2210°+180°
例7、如图，求∠A+∠B + ∠C + ∠D + ∠ E + ∠F + ∠G 的度数。
解：设边数为n,根据题意得:
n为整数，∴ n=15
解：连接CF，设CD，EF的交点为O，
∠D+∠E= ∠DOF= ∠OCF + ∠OFC
∠A+∠B + ∠C + ∠D + ∠ E + ∠F + ∠G就是五边形ABCFG的内角和。
3、正多边形的 相等， 相等
2、四边形有 条对角线．五边形有 条对角线.
1、如图，多边形应记作 边形 ，AB边的邻边是 、 ，顶点E处的内角为 ，过顶点A画出这个多边形的对角线，共有 条，它们把多边形分成 个三角形.
4、八边形的内角和等于 度.
5、一个多边形的内角和等于1260°，这个多边形是 边形.
6、一个多边形的每一个内角都等于135°，则这个多边形是 边形.
7、如图，在△ABC中，∠A=50°，点D、E分别在AB、AC上，则∠1+∠2= 。
∴ ∠B +∠C=130°
∴∠1+∠2=360°-130°=230°
小明想：2008年奥运会在北京召开，设计一个内角和为2008°的多边形图案多有意义，小明的想法能实现吗？为什么？