18.1.1 第2课时平行四边形的对角线的特征人教版八年级数学下册教学课件

这是一份18.1.1 第2课时平行四边形的对角线的特征人教版八年级数学下册教学课件，共16页。

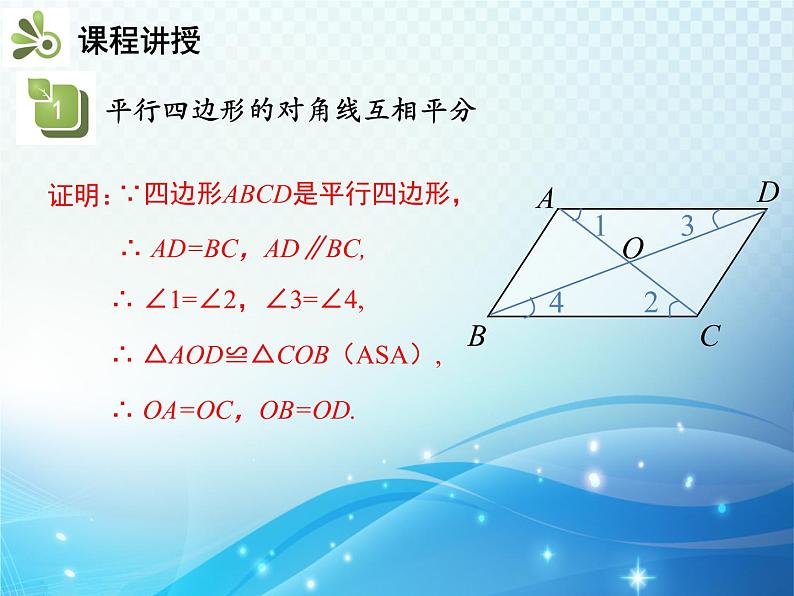
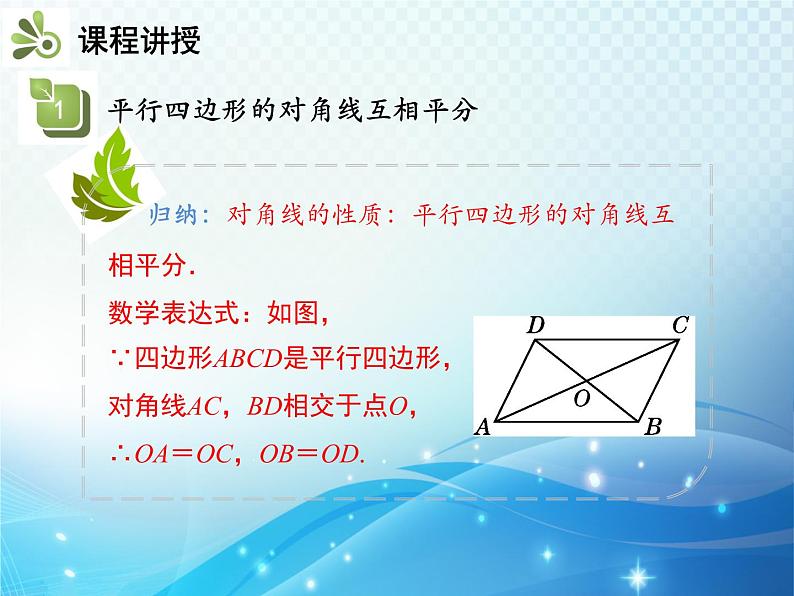
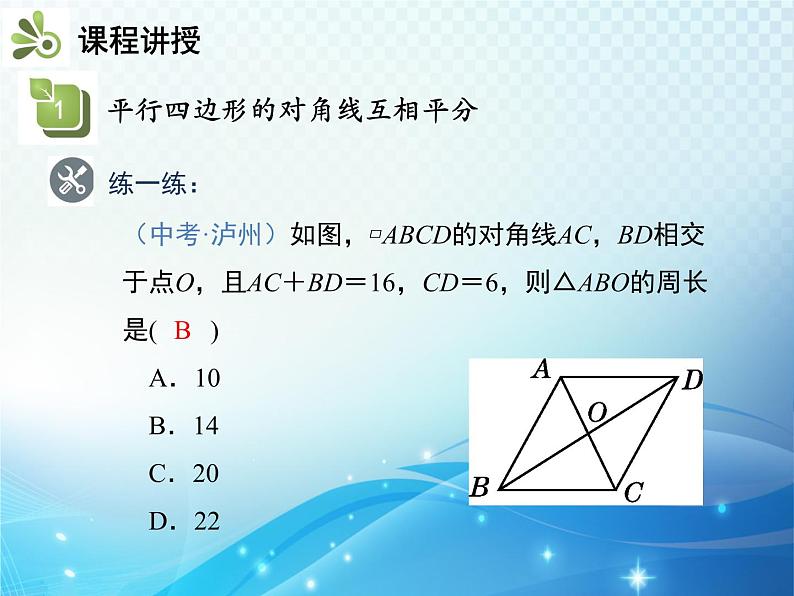
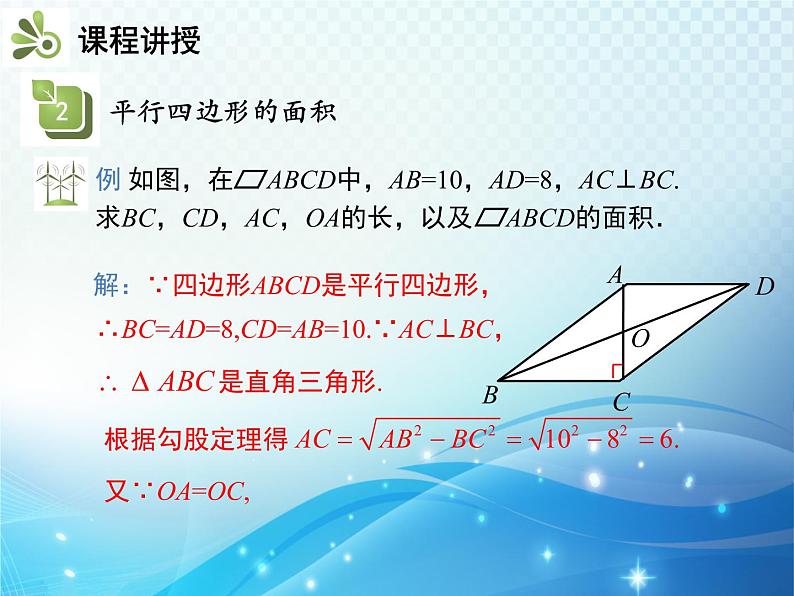
知识要点1.平行四边形的对角线互相平分2.平行四边形的面积我们上节课学习了平行四边形的边、角特征 如图，在□ABCD中，连接AC,BD,并设它们相交于点O. OA与OC,OB与OD有什么关系?你能证明发现的结论吗？∴ AD=BC，AD∥BC, ∴ ∠1=∠2，∠3=∠4,∴ △AOD≌△COB（ASA）,∴ OA=OC，OB=OD.证明：∵四边形ABCD是平行四边形， 归纳：对角线的性质：平行四边形的对角线互相平分．数学表达式：如图，∵四边形ABCD是平行四边形，对角线AC，BD相交于点O，∴OA＝OC，OB＝OD.练一练：（中考·泸州）如图，▱ABCD的对角线AC，BD相交于点O，且AC＋BD＝16，CD＝6，则△ABO的周长是(　　) A．10 B．14 C．20 D．22B解：∵四边形ABCD是平行四边形，根据勾股定理得∴BC=AD=8,CD=AB=10.∵AC⊥BC，又∵OA=OC, 归纳：1．面积公式：平行四边形的面积＝底×高(底为平行四边形的任意一条边，高为这条边与其对边间的距离)．2．等底等高的平行四边形的面积相等．例 如图，若▱ABCD的周长为36 cm，过点D分别作AB，BC边上的高DE，DF，且DE＝4 cm，DF＝5 cm，▱ABCD的面积为(　 　) A．40 cm2 B．32 cm2 C．36 cm2 D．50 cm2A练一练：（中考·包头）如图，过▱ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH，那么图中的▱AEMG的面积S1与▱HCFM的面积S2的大小关系是(　　) A．S1＞S2 B．S1＜S2 C．S1＝S2 D．2S1＝S2C1.（中考·眉山）如图，EF过▱ABCD对角线的交点O，交AD于E，交BC于F，若▱ABCD的周长为18，OE＝1.5，则四边形EFCD的周长为(　　) A．14 B．13 C．12 D．10C2.如图，在▱ABCD中，对角线AC，BD相交于点O，AE⊥BD于点E，CF⊥BD于点F，连接AF，CE，则下列结论：①CF＝AE；②OE＝OF；③DE＝BF；④图中共有四对全等三角形．其中正确结论的个数是(　　) A．4个 B．3个 C．2个 D．1个B3.如图，在平行四边形ABCD中，AC，BD为对角线，BC＝6，BC边上的高为4，则图中阴影部分的面积为(　　) A．3 B．6 C．12 D．24C4.如图，平行四边形ABCD的对角线相交于点O，且AB≠AD，过O作OE⊥BD，交BC于点E.若△CDE的周长为10，则平行四边形ABCD的周长是多少？解：∵四边形ABCD是平行四边形，∴AB=CD，BC=AD，OB=OD.∵OE⊥BD，∴BE=DE.∵△CDE的周长为10，∴DE+CE+CD=BE+CE+CD=BC+CD=10，∴平行四边形ABCD的周长为2×(BC+CD)=20．平行四边形的对角线的特征平行四边形的对角线互相平分平行四边形的面积＝底×高(底为平行四边形的任意一条边，高为这条边与其对边间的距离)．