中职数学高教版（中职）基础模块下册(2021)6.5 直线与圆的位置关系优质教学课件ppt

这是一份中职数学高教版（中职）基础模块下册(2021)6.5 直线与圆的位置关系优质教学课件ppt，共22页。PPT课件主要包含了学习目标，无数组解⇔，一组解⇔，无解⇔，两组解⇔，答消元或降次，所以直线与圆相交，一组解，两组解，方法一联立方程等内容，欢迎下载使用。

第六章 直线与圆的方程 6.5 直线与圆的位置关系
在初中，我们用过“自然数集”“有理数集”等表述，这里的“集”就是集合的简称，那么什么是集合呢？
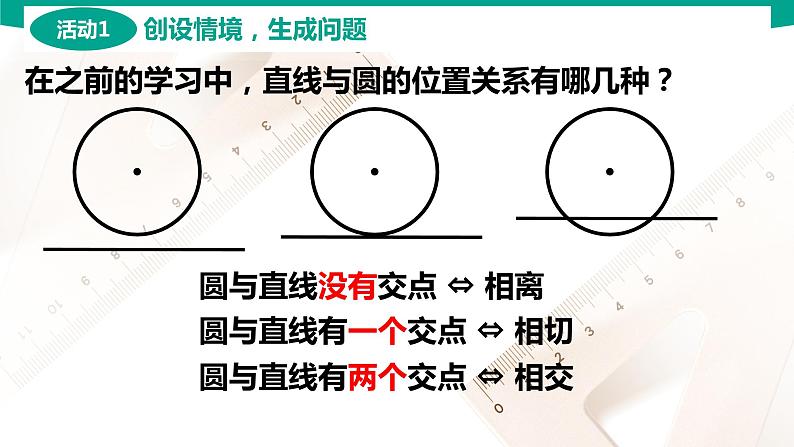
在之前的学习中，直线与圆的位置关系有哪几种？
圆与直线没有交点 ⇔ 相离
圆与直线有一个交点 ⇔ 相切
圆与直线有两个交点 ⇔ 相交
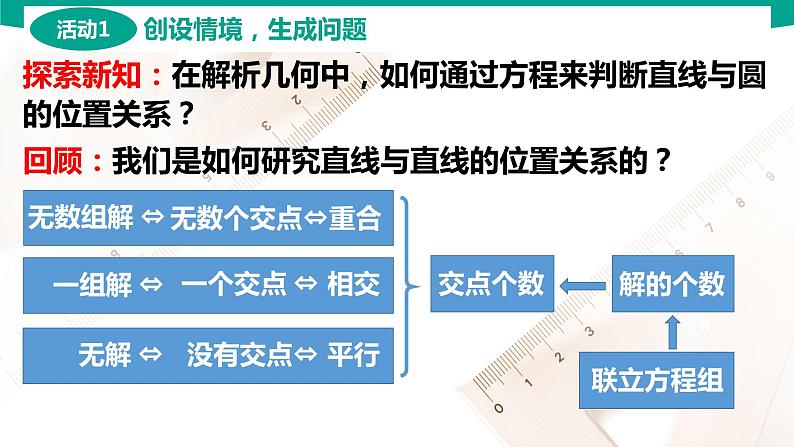
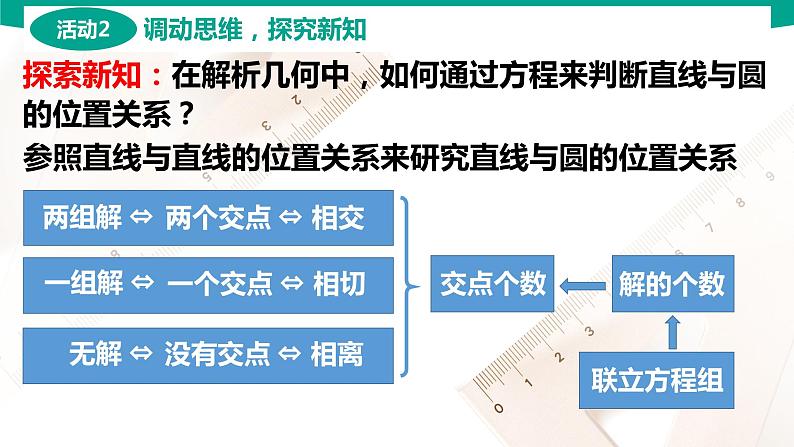
探索新知：在解析几何中，如何通过方程来判断直线与圆的位置关系？
回顾：我们是如何研究直线与直线的位置关系的？
参照直线与直线的位置关系来研究直线与圆的位置关系
练习. 已知直线 ?：3x+y-6=0和圆C：x2+y2-2y-4=0(1). 判断直线 ?与圆C的位置关系.
问：如何判断方程组解的情况？
解：联立直线与圆的方程可得：
将①式变形为y=-3x+6，代入②中得：
x2+(-3x+6)2-2(-3x+6)-4=0
整理得：x2-3x+2=0
问：对于一元二次方程，我们怎么判断它的解的情况？
∆>0⇔方程有2个根⇔有两个交点⇔直线与圆______.
∆=0⇔方程有1个根⇔有一个交点⇔直线与圆______.
∆<0⇔方程无实数根⇔没有交点⇔直线与圆______.
对于方程：x2-3x+2=0，∆=(-3)2-4×1×2=1>0
所以方程x2-3x+2=0有两个根，即方程组有2组解，
联立方程组，消去y得：x2-3x+2=0
例1. 已知直线 ?：3x+y-6=0和圆C：x2+y2-2y-4=0(2). 求直线 ?与圆C的交点.
解得：x1=1，x2=2
将x1与x2代入直线方程可得y1=3，y2=0
所以直线 ?与圆C的交点为(1,3)，(2,0)
刚刚我们用联立方程组，通过方程组解的情况来判断直线与圆的位置关系，那还有没有其他方法呢？
还可以通过圆心到直线的距离d与半径r的大小关系来判断
d>r ⇔直线与圆______.
d=r ⇔直线与圆_____.
d解：将圆C化为一般式得：x2+(y-1)2=5
例1. 已知直线 ?：3x+y-6=0和圆C：x2+y2-2y-4=0(1). 判断直线 ?与圆C的位置关系.
∴ 直线 ?与圆C相交.
直线与圆没有公共点⇔相离
直线与圆有一个公共点⇔ 相切
直线与圆有两个公共点⇔ 相交
判断直线与圆位置关系的方法：
分析：过一点怎么做圆的切线？
点在圆上时可以做一条切线
点在圆外时可以做两条切线
点P在圆上，可以作一条切线.
分析：已知一点P，求过点P的直线方程，
若知道直线的斜率或另一点坐标则可求
回顾：圆的切线垂直于过切点的半径
连接OP，因为直线 ?与圆相切于点P，所以OP⟂?
例3. 过点P(2,1)做圆O：x2+y2=1的切线 ?, 求 ?的方程.
分析：点P与圆心的距离大于半径，所以点P在圆外，可以作两条切线.
此时切点是未知的，如何求直线的方程？
圆的切线与圆有几个交点？
若联立直线与圆的方程，对应一元二次方程的∆应符合什么条件？
已知直线上一点P，应该设直线的什么方程？
设直线的斜率为k，则可用点斜式表示出直线方程.
例3. 过点P(2,1)做圆O：x2+y2=1的切线 ?，求 ?的方程.
解：若?的斜率不存在,则?的方程为x=2
∵ k2+1≠0，且方程只有一个解，∴ ∆=0
此时直线与圆不相切，所以 l 的斜率存在
设?的斜率是k,则?的方程为y-1=k(x-2)
即y=kx+1-2k,代入圆O的方程得：
x2+(kx+1-2k)2=1,化简得(k2+1)x2+(2k-4k2)x+4k2-4k
即(2k-4k2)2-4(k2+1)(4k2-4k)=0，
当k=0时，切线方程为y-1=0(x-2),即y=1
例3. 过点P(2,1)做圆O：x2+y2=1的切线 ?,求 ?的方程.
所以 ?的方程为y=1 或 4x-3y-5=0
该方法运算量比较大，还有其他方法吗？
例3. 过点P(2,1)做圆O：x2+y2=1的切线 ?，求?的方程.
提示：圆的半径就是点O到直线 ?的距离
解：设 ?的斜率是k，则 ?的方程为：y-1=k(x-2),化为一般式：kx-y+1-2k=0
设切点为M，连接OM，则|OM|=r=1
(2). 切点是未知的
利用d=r，运算更简洁.
切线的性质:与圆有一个交点，圆心到切点的距离等于半径.
(1). 若切点是已知的，则利用圆心和切点连线与切线斜率之积为-1求解参数.
方法1：设直线方程，与圆的方程联立,利用∆=0求解参数(不推荐).
方法2：设直线方程，利用d=r求解参数
解：如图,过点C作CD⊥AB于D，连接BC
探究：直线与圆相交(弦长问题)——垂径定理应用
例4. 求圆C:(x-2)2+(y+3)2=4被直线x-y-3=0所截的弦长
则点D是AB的中点，BC=r=2
练4. 圆C的圆心是(-1,b)，半径是3，圆C被直线x-y-1=0所截的弦长为2，则圆的标准方程是____________________.
(x+1)2+(y-2)2=9或(x+1)2+(y+6)2=9
(1). 直线与圆的位置关系：
(2). 求切线方程问题：
d>r ⇔直线与圆相离
d=r ⇔直线与圆相切
d(3). 直线与圆相交：垂径定理.