数学基础模块下册(2021)6.4.1 圆的标准方程优质教学ppt课件

这是一份数学基础模块下册(2021)6.4.1 圆的标准方程优质教学ppt课件，共17页。PPT课件主要包含了学习目标，创设情境生成问题，回顾直线的研究过程，圆心和半径，调动思维探究新知，Mxy，圆的标准方程，3-1，巩固练习提升素养，所以点B不在圆上等内容，欢迎下载使用。

第六章 直线与圆的方程 6.4.1 圆的标准方程
在初中，我们用过“自然数集”“有理数集”等表述，这里的“集”就是集合的简称，那么什么是集合呢？
圆，在生活中处处可见：
多边形和圆，是平面中最常见的图形，本章我们将在平面直角坐标系中研究“圆”.
类比直线的研究过程，如何研究圆的方程？
直线的方程是如何建立的？
在平面直角坐标系中，如何确定一个圆？
回顾圆的定义： 圆是平面内到一个定点的距离等于定长的点的轨迹.
因此，确定一个圆的两个要素是：
类比直线的几何特征，我们可以将圆的几何特征用两点间距离公式的代数形式表达，从而得到圆的方程.
在解析几何中研究轨迹问题时，我们通常采用：“建、设、现、代、化”的方法.
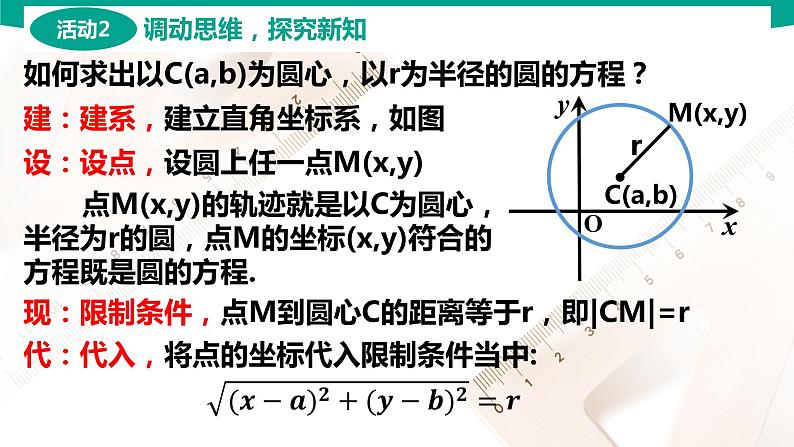
如何求出以C(a,b)为圆心，以r为半径的圆的方程？
建：建系，建立直角坐标系，如图
设：设点，设圆上任一点M(x,y)
点M(x,y)的轨迹就是以C为圆心，半径为r的圆，点M的坐标(x,y)符合的方程既是圆的方程.
现：限制条件，点M到圆心C的距离等于r，即|CM|=r
代：代入，将点的坐标代入限制条件当中:
化：化简，将方程化为简洁而令人舒服的形式.
该方程就是以C(a,b)为圆心，r为半径的圆的方程，叫做：
当圆心与原点重合时，即C(0,0),则圆的标准方程为：
概念巩固：(1). 圆(x-3)2+(y+1)2=16的圆心是_______，半径是____.(2). 圆x2+(y-1)2=22 的圆心是______，半径是_____.(2). 圆x2+y2=8的圆心是______，半径是_____.
例1. 求圆心为C(2,-3)，且经过A(5,1)的圆的标准方程.
分析：要求圆的标准方程，我们需要知道哪些条件？
答：圆心的坐标和半径的长度，圆心是已知的，半径即是点C与点A的距离，即|AC|
所以，圆的标准方程为：(x-2)2+(x+3)2=25
总结：求圆的标准方程，需要确定圆心和半径
所以圆的标准方程是：(x+1)2+y2=4，故选B.
问题：如何确定一个点是否在圆上？
答：将点的坐标代入圆的方程，若方程成立，则点在圆上，否则不在圆上.
练习：点B(-2,-1)在圆C：(x-2)2+(y+3)2=25上吗？
解：将(-2,-1)代入方程得：(-2-2)2+(-1+3)2=20≠25
几何角度：点B到圆心的距离是否等于半径
总结：若一点到圆心的距离是d，圆的半径是r，则：
问：点B(-2,-1)在圆(x-2)2+(y+3)2=25的圆内还是圆外呢？
概念巩固：判断下列点与圆的位置关系(1). 点(1 , -2)，圆(x-1)2+(y-3)2=25(2). 点(2 , 3)，圆(x-5)2+(y+1)2=16(3). 点(3 , -2)，圆(x-5)2+(y+3)2=9
总结：将点的坐标带入标准方程，若：
d=r⇔方程左边=右边(r2)⇔点在圆上
dd>r⇔方程左边＞右边(r2)⇔点在圆外
(2). 圆的一般方程：
(1). 解析几何求点的轨迹的一般思想：“建设现代化”.
(3). 若一点到圆心的距离是d，圆的半径是r，则：