




- 【中考二轮专题复习】2023年中考数学全国通用专题备考试卷——专题01 数学史(原卷版+解析版) 试卷 0 次下载
- 【中考二轮专题复习】2023年中考数学全国通用专题备考试卷——专题03 分母有理化(原卷版+解析版) 试卷 0 次下载
- 【中考二轮专题复习】2023年中考数学全国通用专题备考试卷——专题04 特殊函数(原卷版+解析版) 试卷 0 次下载
- 【中考二轮专题复习】2023年中考数学全国通用专题备考试卷——专题05 定义命题定理与证明(原卷版+解析版) 试卷 0 次下载
- 【中考二轮专题复习】2023年中考数学全国通用专题备考试卷——专题06 整体思想运用(原卷版+解析版) 试卷 0 次下载
【中考二轮专题复习】2023年中考数学全国通用专题备考试卷——专题02 尺规作图(原卷版+解析版)
展开2023年中考数学二轮冲刺精准练新策略(全国通用)
第五篇 中考数学冷门专题
专题02 尺规作图
1.(2022长春)如图,在中,根据尺规作图痕迹,下列说法不一定正确是( )
A. B.
C. D.
【答案】B
【解析】根据尺规作图痕迹,可得DF垂直平分AB,BE是的角平分线,根据垂直平分线的性质和角平分线的定义,直角三角形两锐角互余,等边对等角的性质进行判断即可.
【详解】根据尺规作图痕迹,可得DF垂直平分AB,BE是的角平分线,
,
,
,
综上,正确的是A、C、D选项,
故选:B.
【点睛】本题考查了垂直平分线和角平分线作图,垂直平分线的性质,角平分线的定义,直角三角形两锐角互余,等边对等角的性质,熟练掌握知识点是解题的关键.
2.(2022四川广元)如图,在△ABC中,BC=6,AC=8,∠C=90°,以点B为圆心,BC长为半径画弧,与AB交于点D,再分别以A、D为圆心,大于AD的长为半径画弧,两弧交于点M、N,作直线MN,分别交AC、AB于点E、F,则AE的长度为( )
A. B. 3 C. 2 D.
【答案】A
【解析】由题意易得MN垂直平分AD,AB=10,则有AD=4,AF=2,然后可得,
进而问题可求解.
【详解】由题意得:MN垂直平分AD,,
∴,
∵BC=6,AC=8,∠C=90°,
∴,
∴AD=4,AF=2,,
∴;
故选A.
【点睛】本题主要考查勾股定理、垂直平分线的性质及三角函数,熟练掌握勾股定理、垂直平分线的性质及三角函数是解题的关键.
3.(2022贵州贵阳)如图,已知,点为边上一点,,点为线段的中点,以点为圆心,线段长为半径作弧,交于点,连接,则的长是( )
A. 5 B. C. D.
【答案】A
【解析】根据同圆半径相等可得为等腰三角形,又因为,可得为等边三角形,即可求得BE的长.
连接OE,如图所示:
∵,点为线段的中点,
∴,
∵以点为圆心,线段长为半径作弧,交于点,
∴,
∴,
∴为等边三角形,
即,
故选:A.
【点睛】考查同圆半径相等,一个角为的等腰三角形,解题的关键是判断出为等边三角形.
4.(2022辽宁盘锦)如图,线段是半圆O的直径。分别以点A和点O为圆心,大于的长为半径作弧,两弧交于M,N两点,作直线,交半圆O于点C,交于点E,连接,,若,则的长是( )
A B. 4 C. 6 D.
【答案】A
【解析】【分析】根据作图知CE垂直平分AC,即可得,,根据圆的半径得,,根据圆周角的推论得,根据勾股定理即可得.
【详解】根据作图知CE垂直平分AC,
∴,,
∴,
∴,
即,
∵线段AB是半圆O的直径,
∴,
在中,根据勾股定理得,
,
故选A.
【点睛】本题考查了圆,勾股定理,圆周角推论,解题的关键是掌握这些知识点.
5.(2022辽宁营口)如图,在△ABC中,AB=AC,∠A=36°,由图中的尺规作图得到的射线与AC交于点D,则以下推断错误的是( )
A. B. C. D.
【答案】D
【解析】根据作图过程可得BD平分∠ABC,然后根据等腰三角形的性质即可解决问题.
∵AB=AC,∠A=36°,
∴∠ABC=∠ACB=(180°-36°)=72°,
根据作图过程可知:BD平分∠ABC,
∴∠ABD=∠DBC=∠ABC=36°,
∴∠BDC=180°-36°-72°=72°,∠ADB=∠DBC+∠ACB=36°+72°=108°,故选项C成立;
∵∠BDC=∠ACB=72°,
∴BD=BC,故选项A成立;
∵∠ABD=∠A=36°,
∴AD=BD,故选项B成立;
没有条件能证明CD=AD,故选项D不成立;
故选:D.
【点睛】本题考查了作图-基本作图,等腰三角形的判定和性质,解决本题的关键是掌握基本作图方法.
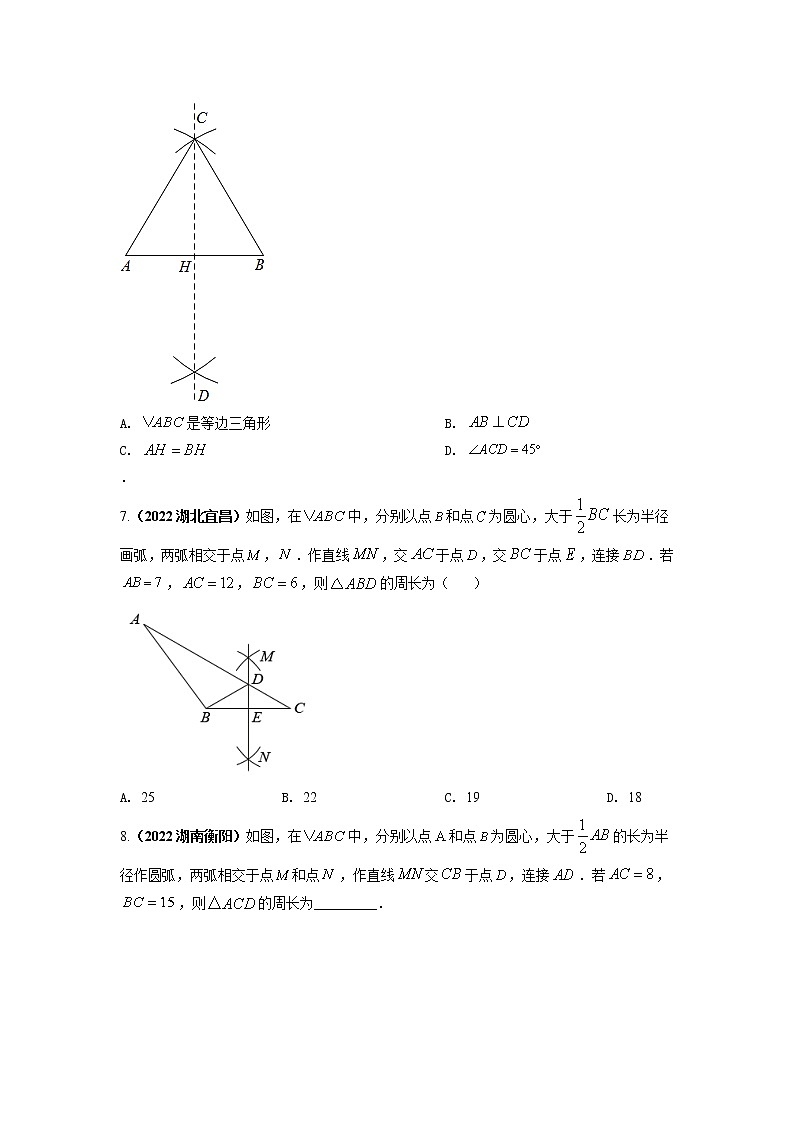
6. (2022湖南湘潭)如图,小明在学了尺规作图后,作了一个图形,其作图步骤是:①作线段,分别以点、为圆心,以长为半径画弧,两弧相交于点、;②连接、,作直线,且与相交于点.则下列说法正确的是( )
A. 是等边三角形 B.
C. D.
【答案】ABC
【解析】根据等边三角形的判定和性质,线段垂直平分线的性质一一判断即可.
由作图可知:AB=BC=AC,
∴△ABC是等边三角形,故A选项正确
∵等边三角形三线合一,
由作图知,CD是线段AB的垂直平分线,
∴,故B选项正确,
∴,,故C选项正确,D选项错误.
故选:ABC.
【点睛】此题考查了作图-基本作图,等边三角形的判定和性质,线段垂直平分线的性质,解题的关键是理解题意,灵活运用所学知识解决问题.
7.(2022湖北宜昌)如图,在中,分别以点和点为圆心,大于长为半径画弧,两弧相交于点,.作直线,交于点,交于点,连接.若,,,则的周长为( )
A. 25 B. 22 C. 19 D. 18
【答案】C
【解析】由垂直平分线的性质可得BD=CD,由△ABD的周长=AB+AD+BD=AB+AD+CD=AB+AC得到答案.
由作图的过程可知,DE是BC的垂直平分线,
∴BD=CD,
∵,,
∴ △ABD的周长=AB+AD+BD
=AB+AD+CD
=AB+AC
=19.
故选:C
【点睛】此题考查了线段垂直平分线的作图、线段垂直平分线的性质、三角形的周长等知识,熟练掌握线段垂直平分线的性质是解题的关键.
8.(2022湖南衡阳)如图,在中,分别以点和点为圆心,大于的长为半径作圆弧,两弧相交于点和点,作直线交于点,连接.若,,则的周长为_________.
【答案】23
【解析】由作图可得:是的垂直平分线,可得再利用三角形的周长公式进行计算即可.
由作图可得:是的垂直平分线,
,,
故答案为:23
【点睛】本题考查的是线段的垂直平分线的作图,线段的垂直平分线的性质,掌握“线段的垂直平分线的性质”是解本题的关键.
9.(2022四川成都)如图,在中,按以下步骤作图:①分别以点和为圆心,以大于的长为半径作弧,两弧相交于点和;②作直线交边于点.若,,,则的长为_________.
【答案】7
【解析】连接EC,依据垂直平分线的性质得.由已知易得,在Rt△AEC中运用勾股定理求得AE,即可求得答案.
【详解】由已知作图方法可得,是线段的垂直平分线,
连接EC,如图,
所以,
所以,
所以∠BEC=∠CEA=90°,
因为,,
所以,
在中,,
所以,
因此的长为7.
故答案为:7.
【点睛】本题主要考查中垂线性质,等腰三角形的性质,勾股定理等知识,解题的关键是掌握中垂线上一点到线段两端点距离相等,由勾股定理求得即可.
10. (2022四川达州)如图,在中,,,分别以点A,B为圆心,大于的长为半径作弧,两弧分别相交于点M,N,作直线,交于点D,连接,则的度数为_____.
【答案】
【解析】根据作图可知,,根据直角三角形两个锐角互余,可得,根据即可求解.
【详解】∵在中,,,
∴,
由作图可知是的垂直平分线,
,
,
,
故答案为:.
【点睛】本题考查了基本作图,垂直平分线的性质,等边对等角,直角三角形的两锐角互余,根据题意分析得出是的垂直平分线,是解题的关键.
11. (2022江苏连云港)如图,在中,.利用尺规在、上分别截取、,使;分别以、为圆心,大于的长为半径作弧,两弧在内交于点;作射线交于点.若,则的长为_________.
【答案】
【解析】如图所示,过点H作HM⊥BC于M,由作图方法可知,BH平分∠ABC,即可证明∠CBH=∠CHB,得到,从而求出HM,CM的长,进而求出BM的长,即可利用勾股定理求出BH的长.
【详解】如图所示,过点H作HM⊥BC于M,
由作图方法可知,BH平分∠ABC,
∴∠ABH=∠CBH,
∵四边形ABCD是平行四边形,
∴,
∴∠CHB=∠ABH,∠C=180°-∠ABC=30°,
∴∠CBH=∠CHB,
∴,
∴,
∴,
∴,
∴,
故答案为:.
【点睛】本题主要考查了角平分线的尺规作图,平行四边形的性质,含30度角的直角三角形的性质,勾股定理,等腰三角形的性质与判定等等,正确求出CH的长是解题的关键.
12.(2022甘肃威武)中国清朝末期的几何作图教科书《最新中学教科书用器画》由国人自编(图1),书中记载了大量几何作图题,所有内容均用浅近的文言文表述,第一编记载了这样一道几何作图题:
原文
释义
甲乙丙为定直角.
以乙为圆心,以任何半径作丁戊弧;
以丁为圆心,以乙丁为半径画弧得交点己;
再以戊为圆心,仍以原半径画弧得交点庚;
乙与己及庚相连作线.
如图2,为直角.
以点为圆心,以任意长为半径画弧,交射线,分别于点,;
以点为圆心,以长为半径画弧与交于点;
再以点为圆心,仍以长为半径画弧与交于点;
作射线,.
(1)根据以上信息,请你用不带刻度的直尺和圆规,在图2中完成这道作图题(保留作图痕迹,不写作法);
(2)根据(1)完成的图,直接写出,,的大小关系.
【答案】(1)见解析 (2)
【解析】【分析】(1)根据题意作出图形即可;
(2)连接DF,EG,可得 和均为等边三角形,,进而可得.
【详解】(1)如图:
(2).
理由:连接DF,EG如图所示
则BD=BF=DF,BE=BG=EG
即和均为等边三角形
∴
∵
∴
【点睛】本题考查了尺规作图,根据题意正确作出图形是解题的关键.
13. (2022陕西)如图,已知是的一个外角.请用尺规作图法,求作射线,使.(保留作图痕迹,不写作法)
【答案】见解析
【解析】作的角平分线即可.
如图,射线即为所求作.
【点睛】本题考查了角平分线、三角形外角的性质、平行线的判定,解题的关键是掌握平行线的判定定理.
14. (2022山东烟台)如图,⊙O是△ABC的外接圆,∠ABC=45°.
(1)请用尺规作出⊙O的切线AD(保留作图痕迹,不写作法);
(2)在(1)的条件下,若AB与切线AD所夹的锐角为75°,⊙O的半径为2,求BC的长.
【答案】(1)见解析 (2)2
【解析】【分析】(1)连接OA,过点A作AD⊥AO即可;
(2)连接OB,OC.先证明∠ACB=75°,再利用三角形内角和定理求出∠CAB,推出∠BOC=120°,求出CH可得结论.
【详解】(1)解:如图,切线AD即为所求;
(2)如图:连接OB,OC.
∵AD是切线,
∴OA⊥AD,
∴∠OAD=90°,
∵∠DAB=75°,
∴∠OAB=15°,
∵OA=OB,
∴∠OAB=∠OBA=15°,
∴∠BOA=150°,
∴∠BCA=∠AOB=75°,
∵∠ABC=45°,
∴∠BAC=180°﹣45°﹣75°=60°,
∴∠BOC=2∠BAC=120°,
∵OB=OC=2,
∴∠BCO=∠CBO=30°,
∵OH⊥BC,
∴CH=BH=OC•cos30°=,
∴BC=2.
【点睛】本题主要考查了作圆的 、三角形的外接圆、切线的判定和性质、解直角三角形等知识点,解题的关键是灵活运用所学知识解决问题.
15. (2022黑龙江绥化)已知:.
(1)尺规作图:用直尺和圆规作出内切圆的圆心O;(只保留作图痕迹,不写作法和证明)
(2)如果的周长为14,内切圆的半径为1.3,求的面积.
【答案】(1)作图见详解
(2)9.1
【解析】【分析】(1)根据角平分线的性质可知角平分线的交点为三角形内切圆的圆心,故只要作出两个角的角平分线即可;
(2)利用割补法,连接OA,OB,OC,作OD⊥AB,OE⊥BC,OF⊥AC,这样将△ABC分成三个小三角形,这三个小三角形分别以△ABC的三边为底,高为内切圆的半径,利用提取公因式可将周长代入,进而求出三角形的面积.
【小问1详解】
解:如下图所示,O为所求作点,
【小问2详解】
解:如图所示,连接OA,OB,OC,作OD⊥AB,OE⊥BC,OF⊥AC,
∵内切圆的半径为1.3,
∴OD=OF=OE=1.3,
∵三角形ABC的周长为14,
∴AB+BC+AC=14,
则
故三角形ABC的面积为9.1.
【点睛】本题考查三角形的内切圆,角平分线的性质,割补法求几何图形的面积,能够将角平分线的性质与三角形的内切圆相结合是解决本题的关键.
16. 如图,四边形ABCD是矩形.
(1)用尺规作线段AC的垂直平分线,交AB于点E,交CD于点F(不写作法,保留作图痕迹);
(2)若BC=4,∠BAC=30°,求BE的长.
【答案】(1)见解析。(2).
【解析】(1)如图所示:
(2)∵四边形ABCD是矩形,EF是线段AC的垂直平分线,
∴AE=EC,∠CAB=∠ACE=30°,
∴∠ECB=60°,
∴∠ECB=30°,
∵BC=4,
∴BE=.
17. 请用直尺、圆规作图,不写作法,但要保留作图痕迹.
已知:∠α,直线l及l上两点A,B.
求作:Rt△ABC,使点C在直线l的上方,且∠ABC=90°,∠BAC=∠α.
【答案】C
【解析】如图,△ABC为所作.
18. 如图,BD是菱形ABCD的对角线,∠CBD=75°,
(1)请用尺规作图法,作AB的垂直平分线EF,垂足为E,交AD于F;(不要求写作法,保留作图痕迹)
(2)在(1)条件下,连接BF,求∠DBF的度数.
【答案】(1)见解析 (2)45°.
【解析】(1)如图所示,直线EF即为所求;
(2)∵四边形ABCD是菱形,
∴∠ABD=∠DBC=∠ABC=75°,DC∥AB,∠A=∠C.
∴∠ABC=150°,∠ABC+∠C=180°,
∴∠C=∠A=30°,
∵EF垂直平分线段AB,
∴AF=FB,
∴∠A=∠FBA=30°,
∴∠DBF=∠ABD﹣∠FBE=45°.
19.(2021湖南怀化)如图,在△ABC中,以A为圆心,任意长为半径画弧,分别交AB、AC于点M、N;再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P;连结AP并延长交BC于点D.则下列说法正确的是( )
A.AD+BD<AB B.AD一定经过△ABC的重心
C.∠BAD=∠CAD D.AD一定经过△ABC的外心
【答案】C
【解析】根据题意判断AD是∠BAC的角平分线,可知C正确,根据重心和外心定义可知B、D选项错误,根据三角形任意两边之和大于第三边可知A错误.
由题可知AD是∠BAC的角平分线,
A、在△ABD中,AD+BD>AB,故选项A错误,不符合题意;
B、△ABC的重心是三条中线的交点,故选项B错误,不符合题意;
C、∵AD是∠BAC的角平分线,∴∠BAD=∠CAD,故选项C正确,符合题意;
D、△ABC的外心是三边中垂线的交点,故选项D错误,不符合题意.
20.(2021浙江杭州)已知线段AB,按如下步骤作图:①作射线AC,使AC⊥AB;③以点A为圆心,AB长为半径作弧;④过点E作EP⊥AB于点P,则AP:AB=( )
A.1: B.1:2 C.1: D.1:
【答案】D
【解析】直接利用基本作图方法得出AP=PE,再结合等腰直角三角形的性质表示出AE,AP的长,即可得出答案.
∵AC⊥AB,
∴∠CAB=90°,
∵AD平分∠BAC,
∴∠EAB=×90°=45°,
∵EP⊥AB,
∴∠APE=90°,
∴∠EAP=∠AEP=45°,
∴AP=PE,
∴设AP=PE=x,
故AE=AB=x,
∴AP:AB=x:x=1:.
21.(2021内蒙古鄂尔多斯)已知:▱AOCD的顶点O(0,0),点C在x轴的正半轴上,按以下步骤作图:
①以点O为圆心,适当长为半径画弧,分别交OA于点M,交OC于点N.
②分别以点M,N为圆心,大于MN的长为半径画弧,两弧在∠AOC内相交于点E.
③画射线OE,交AD于点F(2,3),则点A的坐标为( )
A.(,3) B.(3﹣,3) C.(﹣,3) D.(2﹣,3)
【答案】A
【解析】利用基本作图得到∠AOF=∠COF,再根据平行四边形的性质得到AD∥OC,接着证明∠AOF=∠AFO得到OA=AF,设AF交y轴于M,如图,设A(t,3),则AM=﹣t,AO=AF=﹣t+2,利用勾股定理得到t2+32=(﹣t+2)2,然后解方程求出t即可得到A点坐标.
解:由作法得OE平分∠AOC,则∠AOF=∠COF,
∵四边形AOCD为平行四边形,
∴AD∥OC,
∴∠AFO=∠COF,
∴∠AOF=∠AFO,
∴OA=AF,
设AF交y轴于M,如图,
∵F(2,3),
∴MF=2,OM=3,
设A(t,3),
∴AM=﹣t,AO=AF=﹣t+2,
在Rt△OAM中,t2+32=(﹣t+2)2,解得t=﹣,
∴A(﹣,3).
故选:A.
22. (2021辽宁盘锦)如图,已知直线AB和AB上的一点C,过点C作直线AB的垂线,步骤如下:
第一步:以点C为圆心,以任意长为半径作弧,交直线AB于点D和点E;
第二步:分别以点D和点E为圆心,以为半径作弧,两弧交于点F;
第三步:作直线CF,直线CF即为所求.
下列关于的说法正确的是( )
A. ≥ B. ≤ C. D.
【答案】C
【解析】根据过直线外一点作已知直线的垂线的步骤,结合三角形三边关系判断即可.
由作图可知,分别以点和点为圆心,以为半径作弧,两弧交于点,此时.
【点睛】本题考查作图基本作图,解题的关键是理解题意,灵活运用所学知识解决问题.
23.(2021湖北黄石)如图,在Rt△ABC中,∠ACB=90°,按以下步骤作图:①以B为圆心,任意长为半径作弧,分别交BA、BC于M、N两点;②分别以M、N为圆心,以大于MN的长为半径作弧,两弧相交于点P;③作射线BP,交边AC于D点.若AB=10,BC=6,则线段CD的长为( )
A.3 B. C. D.
【答案】A
【解析】利用基本作图得BD平分∠ABC,过D点作DE⊥AB于E,如图,根据角平分线的性质得到则DE=DC,再利用勾股定理计算出AC=8,然后利用面积法得到•DE×10+•CD×6=×6×8,最后解方程即可.
解:由作法得BD平分∠ABC,
过D点作DE⊥AB于E,如图,则DE=DC,
在Rt△ABC中,AC===8,
∵S△ABD+S△BCD=S△ABC,
∴•DE×10+•CD×6=×6×8,
即5CD+3CD=24,
∴CD=3.
故选:A.
24.(2021湖南邵阳)如图,已知线段AB长为4.现按照以下步骤作图:
①分别以点A,B为圆心,大于AB长为半径画弧,两弧分别相交于点E,F;
②过E,F两点作直线,与线段AB相交于点O.
则AO的长为 .
【答案】2
【解析】直接利用基本作图方法得出EF垂直平分AB,即可得出答案.
由基本作图方法可得:EF垂直平分AB,
∵AB=4,
∴AO=AB=2.
25.(2022福建)如图,BD是矩形ABCD的对角线.
(1)求作⊙A,使得⊙A与BD相切(要求:尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,设BD与⊙A相切于点E,CF⊥BD,垂足为F.若直线CF与⊙A相切于点G,求的值.
【答案】(1)作图见解析 (2)
【解析】【分析】(1)先过点A作BD的垂线,进而找出半径,即可作出图形;
(2)根据题意,作出图形,设,⊙A的半径为r,先判断出BE=DE,进而得出四边形AEFG是正方形,然后在Rt△ABE中,根据勾股定理建立方程求解,再判定,根据,,在Rt△ADE中,利用,得到,求解得到tan∠ADB的值为.
【小问1详解】
解:如图所示,⊙A即所求作:
【小问2详解】
解:根据题意,作出图形如下:
设,⊙A的半径为r,
∵BD与⊙A相切于点E,CF与⊙A相切于点G,
∴AE⊥BD,AG⊥CG,即∠AEF=∠AGF=90°,
∵CF⊥BD,
∴∠EFG=90°,
∴四边形AEFG是矩形,
又,
∴四边形AEFG是正方形,
∴,
在Rt△AEB和Rt△DAB中,,,
∴,
在Rt△ABE中,,
∴,
∵四边形ABCD是矩形,
∴,AB=CD,
∴,又,
∴,
,
∴,
在Rt△ADE中,,即,
∴,即,
∵,
∴,即tan∠ADB的值为.
【点睛】此题是圆的综合题,主要考查了尺规作图,切线的性质,全等三角形的判定和性质,正方形的判定与性质,矩形的判定与性质,勾股定理,锐角三角函数,利用三角函数得出线段长建立方程是解决问题的关键.
26.(2021广西贵港)尺规作图(只保留作图痕迹,不要求写出作法).如图,已知△ABC,且AB>AC.
(1)在AB边上求作点D,使DB=DC;
(2)在AC边上求作点E,使△ADE∽△ACB.
【答案】见解析。
【解析】(1)作线段BC的垂直平分线交AB于点D,连接CD即可.
(2)作∠ADT=∠ACB,射线DT交AC于点E,点E即为所求.
解:(1)如图,点D即为所求.
(2)如图,点E即为所求.
【中考二轮专题复习】2023年中考数学全国通用专题备考试卷——专题02 韦达定理问题(原卷版+解析版): 这是一份【中考二轮专题复习】2023年中考数学全国通用专题备考试卷——专题02 韦达定理问题(原卷版+解析版),文件包含专题02韦达定理问题解析版docx、专题02韦达定理问题原卷版docx等2份试卷配套教学资源,其中试卷共12页, 欢迎下载使用。
【中考二轮专题复习】2023年中考数学全国通用专题备考试卷——专题04 特殊函数(原卷版+解析版): 这是一份【中考二轮专题复习】2023年中考数学全国通用专题备考试卷——专题04 特殊函数(原卷版+解析版),文件包含专题04特殊函数解析版docx、专题04特殊函数原卷版docx等2份试卷配套教学资源,其中试卷共9页, 欢迎下载使用。
【中考二轮专题复习】2023年中考数学全国通用专题备考试卷——专题01 数学史(原卷版+解析版): 这是一份【中考二轮专题复习】2023年中考数学全国通用专题备考试卷——专题01 数学史(原卷版+解析版),文件包含专题01数学史解析版docx、专题01数学史原卷版docx等2份试卷配套教学资源,其中试卷共23页, 欢迎下载使用。













