山东省济宁市金乡县2022-2023学年九年级上学期期末考试数学试题（含答案）

这是一份山东省济宁市金乡县2022-2023学年九年级上学期期末考试数学试题（含答案），共16页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

（考试时间为120分钟，满分100分）
一、单选题(每题3分，共30分)
1．下列绿色能源图标中既是轴对称图形又是中心对称图形的是（ ）.
A．B．C．D．
2．如图，在中，弦，相交于点，，，则的大小是（ ）.
A．35°
B．45°
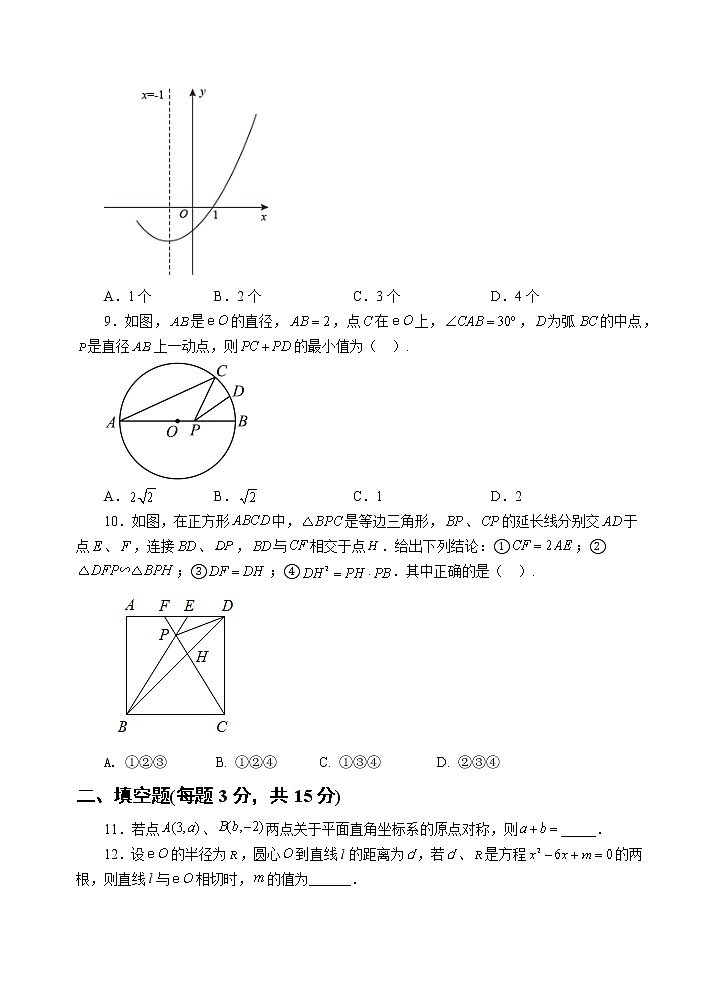
C．60°
D．70°
3．已知点，，都在反比例函数的图象上，则（ ）.
A．B．C．D．
4．“读万卷书，行万里路．”某校为了丰富学生的阅历知识，坚持开展课外阅读活动，学生人均阅读量从七年级的每年100万字增加到九年级的每年121万字．设该校七至九年级人均阅读量年均增长率为x，则可列方程为（ ）.
A．B．
C．D．
5．在边长为1的小正方形组成的网格中，有如图所示的A，B两点，在格点上任意放置点C，恰好能使得△ABC的面积为1的概率为（ ）.
A． B．
C． D．
6．如图，在等腰三角形ABC中，AB=AC=5，BC=6，点D为BC的中点，DE⊥AB于点E，则cs∠BDE的值等于（ ）.
A．B．
C．D．
7．如图，点A在反比例函数的图像上，点B在轴负半轴上，直线交轴于点C，若，的面积为3，则的值为（ ）.
A．6B．5C．3D．2
8．如图，二次函数图象的一部分与x轴的一个交点坐标为，对称轴为直线，结合图象给出下列结论：①；②；③若关于x的一元二次方程的一根是3，则另一根是；④若点，，均在二次函数图象上，则．其中正确的结论的个数为（ ）．
A．1个B．2个C．3个D．4个
9．如图，是的直径，，点在上，，为弧的中点，是直径上一动点，则的最小值为（ ）.
A．B．C．1D．2
10．如图，在正方形中，是等边三角形，、的延长线分别交于点、，连接、，与相交于点．给出下列结论：①；②；③；④．其中正确的是（ ）.
①②③ B. ①②④ C. ①③④ D. ②③④
二、填空题(每题3分，共15分)
11．若点、两点关于平面直角坐标系的原点对称，则_____．
12．设的半径为，圆心到直线l的距离为，若、是方程的两根，则直线l与相切时，的值为______．
13．如图，小明同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的位置，O设法使斜边DF保持水平，并且边DE与点B在同一直线上．已知纸板的两条边DF＝50cm，EF＝30cm，测得边DF离地面的高度AC＝1.5m，CD＝20m，则树高AB为_____．
14．如图，A是双曲线上的一点，点C是OA的中点，过点C作y轴的垂线，垂足为D，交双曲线于点B，则△ABD的面积是___________．
15．如图，在平面直角坐标系中，点A在y轴的正半轴上，，将绕点O顺时针旋转到，扫过的面积记为，交x轴于点；将绕点O顺时针旋转到，扫过的面积记为，交y轴于点；将绕点O顺时针旋转到，扫过的面积记为，交x轴于点；…；按此规律，则S2023的值为 _____．
O
三、解答题(共55分)
16．(本题6分)计算：
(1) (2)解方程：
17．(本题7分)如图，的顶点坐标分别为，，．
(1)画出关于y轴对称的；
(2)将绕点C顺时针旋转，得到，在图中画出；
(3)求出点B所经过的路径弧的长．（结果保留π）
18．(本题7分)如图，中，，，点，点，反比例函数的图象经过点A．
（1）求反比例函数的解析式；
（2）将直线向上平移个单位后经过反比例函数图象上的点，求，的值．
19．(本题5分)一艘观光游船从港口A以北偏东60°的方向出港观光，航行80海里至C处时发生了侧翻沉船事故，立即发出了求救信号，一艘在港口正东方向的海警船接到求救信号，测得事故船在它的北偏东37°方向，马上以40海里每小时的速度前往救援，求海警船到达事故船C处所需的大约时间．（温馨提示：sin53°≈0.8，cs53°≈0.6）
20．(本题9分)某书店以每本30元的价格购进一批图书进行销售，物价局根据市场行情规定这种图书的销售单价不低于42元且不高于62元．在销售中发现，该种图书每天的销售数量y（本）与销售单价x（元）之间存在一次函数关系，对应如表：
(1)求出y与x之间的函数关系式；
(2)请问该种图书每天的销售利润w（元）的最大值是多少？
(3)如果该种图书每天的销售利润必须不少于600元，试确定该种图书销售单价x的范围．
21．(本题9分)如图，是直径，点是上一点，，点为延长线上一点，且．
(1)求证：是的切线；
(2)过点作交于点，的延长线交于点，若的直径为2，求线段的长．
22．(本题12分)如图，抛物线与轴交于点，，与轴交于点，点是线段上方抛物线上的一个动点．
(1)求抛物线的解析式；
(2)当点运动到什么位置时，的面积最大？
(3)过点作轴的垂线，交线段于点，再过点作轴交抛物线于点，连接．是否存在点，使为等腰直角三角形？若存在，求点的坐标；若不存在，请说明理由。
销售单价x（元）
43
45
47
49
…
销售数量y（本）
54
50
46
42
…
2022—2023学年度第一学期第二次学情监测
九年级数学答题纸
选择题（每题3分，共30分）
非选择题（请在各试题的答题区内作答）
九年级数学参考答案
一、选择题（共10小题，每小题3分，共30分）
1．D 2．A 3．B 4．A 5．C 6．D 7．C 8．C 9．B 10．B
填空题（共5小题，每小题3分，共15分）
11． 12． 9 13． 16.5m． 14． 4 15． 22019π
解答题（共7小题，共55分）
16．（1）解：； ……3分
（2）解：，，，
解得，， ……………………………6分
17．（1）解：如图所示，即为所求； ……………………………2分
解：如图所示，即为所求；……4分
（3）解：∵，……5分
∴点B所经过的路径弧的长． ……………………………7分
18．（1）如图，作轴，则
，，
……………………………2分
点，点，
∴OD=OC+CD=6，代入中，． ………4分
（2）在上，设直线OA解析式为
， ………………5分
直线向上平移个单位后的解析式为： 图象经过（1，12）
解得：，． …………7分
19．解：如图，过点C作CD⊥AB交AB延长线于D．在Rt△ACD中，∵∠ADC=90°，∠CAD=30°，AC=80海里，∴CD=AC=40海里． ……………………………2分
在Rt△CBD中，∵∠CDB=90°，∠CBD=90°﹣37°=53°，
∴BC=≈=50（海里）， ………4分
∴海警船到达事故船C处所需的时间大约为：50÷40=（小时）． ………………5分
20．（1）解：设解析式为： ， ……………………………1分
将x=43，y=54；x=45，y=50代入解析式得： ，解得： ，
，由题意得：，（）…………3分
（2）根据题意得∶ ， ……………………………4分
整理得： ， ……………………5分
，∴当x=50时，w有最大值为800元，
∴该种图书每天的销售利润的最大值是800元； …………………………6分
（3）当w=600时，可得： ， …………………………7分
解得：（舍） ， ……………………………8分
由二次函数的图象可得：当 时，该种图书每天的销售利润不少于600元．…9分
21．（1）证明：连接，如图，
∵，，∴．
∵∴． ………2分
∴．即，
∵是圆的半径，∴是的切线； ………4分
（2）解：∵， ∴． ∴．∴． ………6分
∵的直径为2，∴．∴． ……………7分
∵，∴．∴．
∵，，∴．∴．
∴．∴．………………………9分
22．（1）解：抛物线与轴交于点，，，
解得，， 抛物线的解析式为． …………2分
（2）如图1，作于点，交于点，作于点，令，得∴； …………3分
设直线的解析式为，，，
， ……………………………4分
设，其中，则，
， ………5分
， ……………………………7分
当时，的面积有最大值；，
点运动到时，的面积最大； ……………………………8分
（3）存在，或， ……………………………9分
如图，轴
若为等腰直角三角形，则，=………10分
设点的横坐标为，点的横坐标为，
，，
，
又，
， ……………………………11分
解得：或，或．………12分
填空题（每题3分，共15分）
11 ，12 ，13 ，14 ，15 .
16．(本题满分6分)
(1)； (2)解方程：．
17.（本题满分7分）
(3)
18．（本题满分7分)
（1）

（2）

19．（本题满分5分）

20．（本题满分9分）
（1）


（2）
（3）

21．（本题满分9分）
（1）
（2）
22．（本题满分11分）
（1）

（2）
（3）