湘教版九年级下册1.3 不共线三点确定二次函数的表达式精品课件ppt

*1.3 不共线三点确定二次函数的表达式

【知识与技能】

1.掌握用待定系数法列方程组求二次函数解析式.

2.由已知条件的特点,灵活选择二次函数的三种形式，合适地设置函数解析式,可使计算过程简便.

【过程与方法】

通过例题讲解使学生初步掌握,用待定系数法求二次函数的解析式.

【情感态度】

通过本节教学,激发学生探究问题,解决问题的能力.

【教学重点】

用待定系数法求二次函数的解析式.

【教学难点】

灵活选择合适的表达式设法.

一、情境导入，初步认识

1.同学们想一想，已知一次函数图象上两个点的坐标，如何用待定系数法求它的解析式？

学生回答：

2.已知二次函数图象上有两个点的坐标，能求出其解析式吗？三个点的坐标呢？

二、思考探究，获取新知

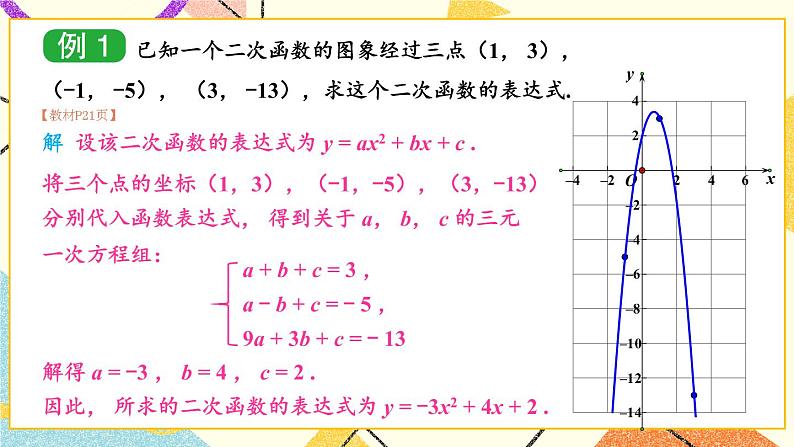
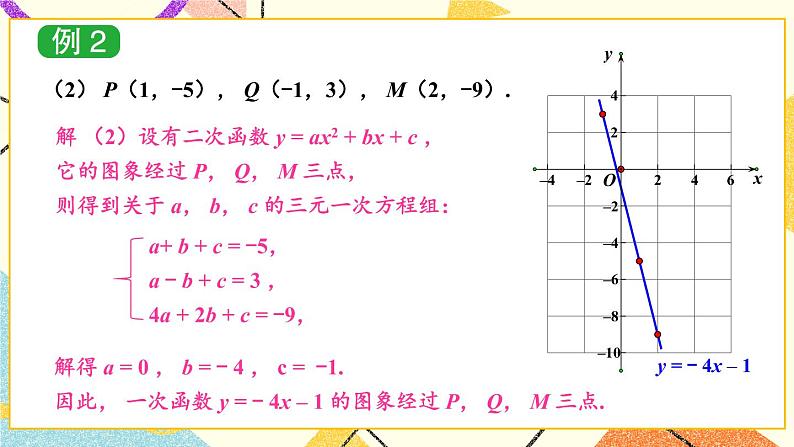
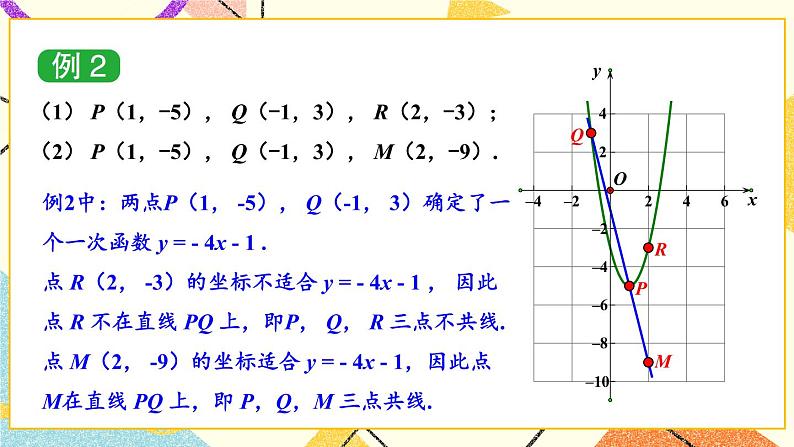
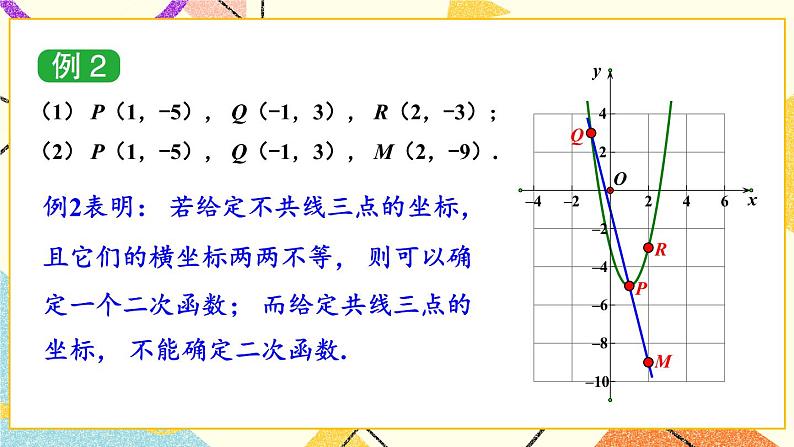
探究1  已知三点求二次函数解析式讲解：教材P21例1，例2.

【教学说明】让学生通过例题讲解归纳出已知三点坐标求二次函数解析式的方法.

探究2  用顶点式求二次函数解析式.

例3  已知二次函数的顶点为A(1,-4)且过B(3,0),求二次函数解析式.

【分析】已知抛物线的顶点,设二次函数的解析式为y=a(x-h)2+k.

解：∵抛物线顶点为A(1,-4),∴设抛物线解析式为y=a(x-1)2-4,∵点B（3，0）在图象上，∴0=4a-4,∴a=1,∴y=(x-1)2-4,即y=x2-2x-3.

【教学说明】已知顶点坐标，设顶点式比较方便，另外已知函数的最（大或小）值即为顶点纵坐标，对称轴与顶点横坐标一致.

探究3  用交点式求二次函数解析式

例4(甘肃白银中考) 已知一抛物线与x轴交于点A（-2，0），B（1，0），且经过点C（2，8）.求二次函数解析式.

【分析】由于抛物线与x轴的两个交点为A（-2，0），B（1，0），可设解析式为交点式：y=a(x-x1)(x-x2).

解：A（-2，0），B（1，0）在x轴上，设二次函数解析式为y=a(x+2)(x-1).又∵图象过点C（2，8），∴8=a(2+2)(2-1),∴a=2,∴y=2(x+2)(x-1)=2x2+2x-4.

【教学说明】因为已知点为抛物线与x轴的交点，解析式可设为交点式，再把第三点代入可得一元一次方程，较一般式所得的三元一次方程简单.

三、运用新知，深化理解

1.若二次函数y=-x2+mx-2的最大值为 ，则m的值为（      ）

A.17    B.1    C.±17    D.±1

2.二次函数y=ax2+bx+c的图象大致如图所示，下列判断错误的是（      ）

A.a＜0    B.b＞0    C.c＞0    D.ab＞0

3.如图，抛物线y=ax2+bx+c(a＞0)的对称轴是直线x=1,且经过点P（3,0)，则a-b+c的值为（      ）

A.0    B.-1    C.1    D.2

4.如图是二次函数y=ax2+3x+a2-1的图象,a的值是        .

5.已知二次函数的图象经过点（0，3），（-3，0），（2，-5），且与x轴交于A、B两点.

(1)试确定此二次函数的解析式;

(2)判断点P(-2,3)是否在这个二次函数的图象上?如果在,请求出△PAB的面积;如果不在,试说明理由.

【教学说明】通过练习巩固加深对新知的理解,并适当对题目作简单的提示.第3题根据二次函数图象的对称性得知图象与x轴的另一交点坐标为（-1，0），将此点代入解析式，即可求出a-b+c的值.第4题可根据图象经过原点求出a的值，再考虑开口方向.

【答案】1.C  2.D  3.A  4.-15.

解:(1)设二次函数的解析式为y=ax2+bx+c.∵二次函数的图象经过点（0，3），（-3，0），（2，-5）.∴c=3.∴9a-3b+3=0,4a+2b+3=-5.解得a=-1,b=-2.∴二次函数的解析式为y=-x2-2x+3.

(2)∵当x=-2时，y=-(-2)2-2×(-2)+3=3,∴点P（-2,3)在这个二次函数的图象上.令-x2-2x+3=0,∴x1=-3,x2=1.∴与x轴的交点为(-3,0),(1,0),∴AB=4.即S△PAB=12×4×3=6.

四、师生互动，课堂小结

1.这节课你学到了什么？还有哪些疑惑？

2.在学生回答的基础上，教师点评：

3.求二次函数解析式的三种表达式的形式.

(1)已知三点坐标,设二次函数解析式为y=ax2+bx+c.

(2)已知顶点坐标：设二次函数解析式为y=a(x-h)2+k.

(3)已知抛物线与x轴两交点坐标为(x1,0),(x2,0)可设二次函数解析式为y=a(x-x1)(x-x2).

1.教材P23第1~3题.

2.完成同步练习册中本课时的练习.

用待定系数法求二次函数的表达式有三种基本方法,解题时可根据不同的条件灵活选用.本节内容是二次函数中的重点也是中考考点之一,同学们要通过练习,熟练掌握.