【中考一轮复习】2023年中考数学通用版考点梳理+练习——第25讲 与圆有关的位置关系（含答案）

这是一份【中考一轮复习】2023年中考数学通用版考点梳理+练习——第25讲 与圆有关的位置关系（含答案），共7页。

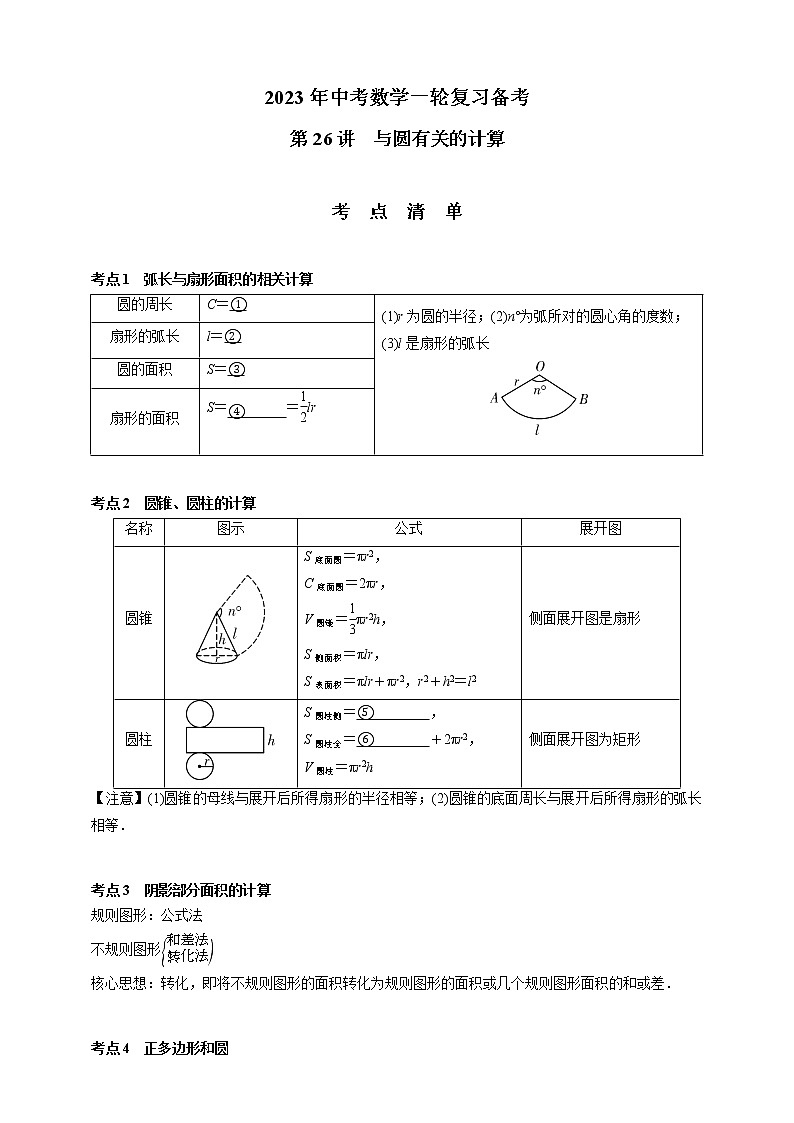
考 点 清 单
考点1 弧长与扇形面积的相关计算
考点2 圆锥、圆柱的计算
【注意】(1)圆锥的母线与展开后所得扇形的半径相等；(2)圆锥的底面周长与展开后所得扇形的弧长相等．
考点3 阴影部分面积的计算
规则图形：公式法
不规则图形eq \b\lc\{(\a\vs4\al\c1(和差法,转化法))
核心思想：转化，即将不规则图形的面积转化为规则图形的面积或几个规则图形面积的和或差．
考点4 正多边形和圆
1．中心角：正多边形每一边所对的圆心角叫做正多边形的中心角．
若n为正多边形的边数，α为中心角，则α＝⑦ .
2．边心距：中心到正多边形的一边的距离叫做正多边形的边心距，如图，OP为边心距．
3．如图，r(边心距)、R(半径)、a(正多边形的边长)的关系：r2＋(eq \f(a,2))2＝R2.
强 化 演 练
基础练
1．若扇形的半径为3，圆心角为60°， 则此扇形的弧长是( )
A．eq \f(1,2)π B．π C．eq \f(3,2)π D．2π
2．用半径为30 cm，圆心角为120°的扇形纸片恰好能围成一个圆锥的侧面，则这个圆锥底面半径为( )
A．5 cm B．10 cm C．15 cm D．20 cm
3．一根钢管放在V形架内，其横截面如图所示，钢管的半径是24 cm，若∠ACB＝60°，则劣弧AB的长是( )
A．8π cm B．16π cm C．32π cm D．192π cm
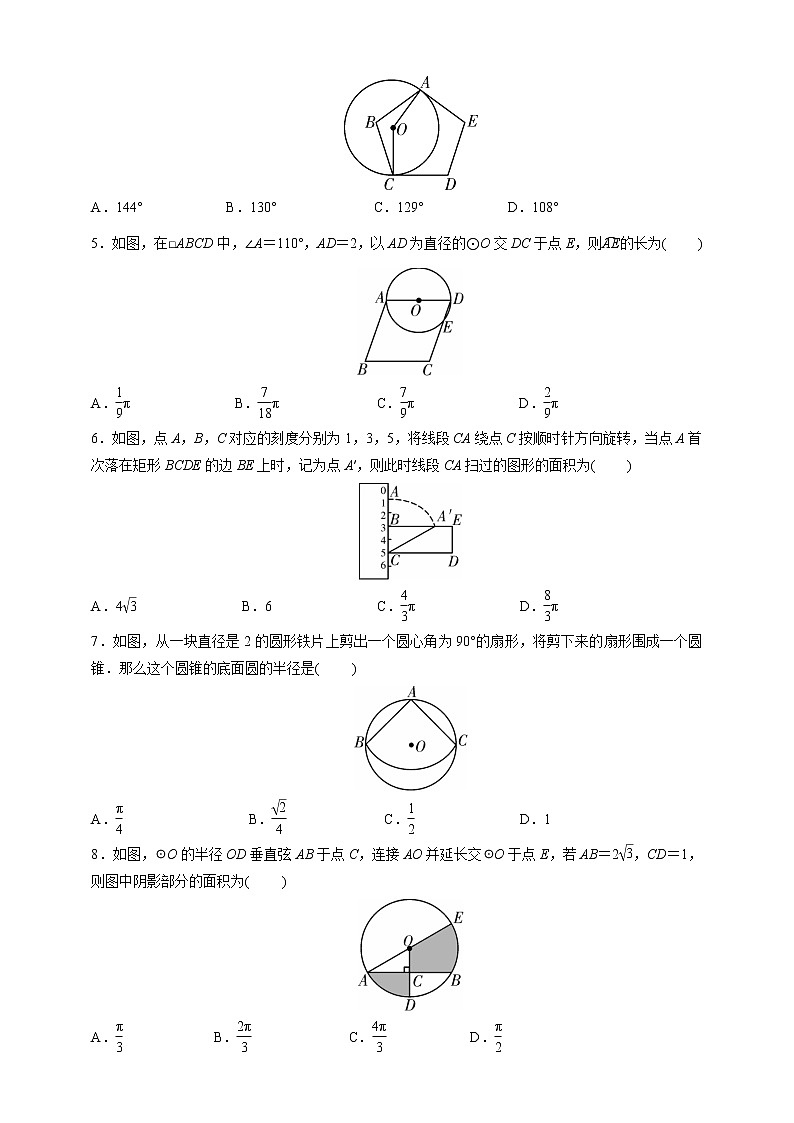
4．如图，⊙O与正五边形ABCDE的两边AE，CD相切于A，C两点，则∠AOC的度数是( )
A．144° B．130° C．129° D．108°
5．如图，在□ABCD中，∠A＝110°，AD＝2，以AD为直径的⊙O交DC于点E，则eq \(AE,\s\up10(︵))的长为( )
A．eq \f(1,9)π B．eq \f(7,18)π C．eq \f(7,9)π D．eq \f(2,9)π
6．如图，点A，B，C对应的刻度分别为1，3，5，将线段CA绕点C按顺时针方向旋转，当点A首次落在矩形BCDE的边BE上时，记为点A′，则此时线段CA扫过的图形的面积为( )
A．4eq \r(3) B．6 C．eq \f(4,3)π D．eq \f(8,3)π
7．如图，从一块直径是2的圆形铁片上剪出一个圆心角为90°的扇形，将剪下来的扇形围成一个圆锥．那么这个圆锥的底面圆的半径是( )
A．eq \f(π,4) B．eq \f(\r(2),4) C．eq \f(1,2) D．1
8．如图，☉O的半径OD垂直弦AB于点C，连接AO并延长交☉O于点E，若AB＝2eq \r(3)，CD＝1，则图中阴影部分的面积为( )
A．eq \f(π,3) B．eq \f(2π,3) C．eq \f(4π,3) D．eq \f(π,2)
9．如图，公园内有一个半径为18米的圆形草坪，从A地走到B地有观赏路(劣弧AB)和便民路(线段AB)．已知A，B是圆上的点，O为圆心，∠AOB＝120°，小强从A走到B，走便民路比走观赏路少走( )
A．6π－6eq \r(3)米 B．6π－9eq \r(3)米
C．12π－9eq \r(3)米 D．12π－18eq \r(3)米
10．如图，△ABC内接于⊙O，∠BAC＝60°，BC＝6，则eq \(BC,\s\up10(︵))的长为( )
A．eq \f(2\r(3),3)π B．eq \f(4\r(3),3)π C．π D．eq \f(4,3)π
11．如图，圆锥的高是4，它的侧面展开图是圆心角为120°的扇形，则圆锥的侧面积是 (结果保留π)．
12．如图，已知四边形ABCD是⊙O的内接四边形，且△ADE 是等边三角形，⊙O的半径为2.则劣弧BD的长为 .
13．如图，在△ABC中， AB＝AC＝2.以AB为直径的⊙O，交AC于点E，交BC于点D.若劣弧DE的长为eq \f(π,6)，则∠BAC＝ .
14．如图，矩形ABCD的对角线AC，BD交于点O，分别以点A，C为圆心，AO长为半径画弧，分别交AB，CD于点E，F.若BD＝4，∠CAB＝36°，则图中阴影部分的面积为 .(结果保留π)
15．如图，⊙O的直径AB＝6，圆内接三角形ACD中，AC＝CD，∠CAD＝ 30°，则图中阴影部分的面积为 .
16．如图1，四边形ABCD内接于⊙O，AD为直径，过点C作CE⊥AB于点E，连接AC.
(1)求证：∠CAD＝∠ECB；
(2)若CE是⊙O的切线，∠CAD＝30°，连接OC，如图2.
①请判断四边形ABCO的形状，并说明理由；
②当AB＝2时，求AD，AC与eq \(CD,\s\up10(︵))围成阴影部分的面积．

强化练
17．如图，正方形ABCD内接于⊙O，线段MN在对角线BD上运动，若⊙O的面积为2π，MN＝1，则△AMN周长的最小值是( )
A．3 B．4 C．5 D．6
18．如图，在Rt△ABC中，∠ABC＝40°，AB＝6，斜边AB是半圆O的直径，点D是半圆上的一个动点，连接CD与AB交于点E，若△BCE是等腰三角形，则弧BD的长为( )
A．eq \f(4,3)π B．eq \f(2,3)π或eq \f(3,7)π C．eq \f(4,3)π或eq \f(7,3)π D．eq \f(7,3)或eq \f(7,6)π
19．如图，在边长为4的正方形ABCD中，以AB为直径的半圆交对角线AC于点E，以C为圆心、BC长为半径画弧交AC于点F，则图中阴影部分的面积是 .
提升练
20．如图，作⊙O的任意一条直经FC，分别以F，C为圆心，以FO的长为半径作弧，与⊙O相交于点E，A和D，B，顺次连接AB，BC，CD，DE，EF，FA，得到六边形ABCDEF，则⊙O的面积与阴影区域的面积的比值为 .
参 考 答 案
考点清单
①2πr ②eq \f(nπr,180) ③πr2 ④eq \f(nπr2,360) ⑤2πrh ⑥2πrh ⑦eq \f(360°,n)
强化演练
1. B 2. B 3. B 4. A 5. C 6. D 7. B 8. C 9. D 10. B 11. 6π
12. eq \f(4,3)π 13. 3
° 14. eq \f(4,5)π 15. 3π－eq \f(9\r(3),2)
16. (1)证明：∵四边形ABCD是⊙O的内接四边形，∴∠CBE＝∠D. ∵AD为⊙O的直径，∴∠ACD＝90°，∴∠D＋∠CAD＝90°，∴∠CBE＋∠CAD＝90°. ∵CE⊥AB，∴∠CBE＋∠BCE＝90°，∴∠CAD＝∠ECB.
(2)解：①四边形ABCO是菱形，理由：∵∠CAD＝30°，∴∠COD＝2∠CAD＝60°，∠D＝90°－∠CAD＝60°. ∵CE是⊙O的切线，∴OC⊥CE.∵CE⊥AB，∴OC∥AB，∴∠DAB＝∠COD＝60°. 由(1)知，∠CBE＋∠CAD＝90°，∴∠CBE＝90°－∠CAD＝60°＝∠DAB，∴BC∥OA，∴四边形ABCO是平行四边形．∵OA＝OC，∴□ABCO是菱形．
②由①知四边形ABCO是菱形，∴OA＝OC＝AB＝2，∴AD＝2OA＝4. 由①知∠COD＝60°，在Rt△ACD中，∠CAD＝30°，∴CD＝2，AC＝2eq \r(3)，∴AD，AC与eq \(CD,\s\up10(︵))围成阴影部分的面积为S△ACO＋S扇形COD＝eq \f(1,2)S△ACD＋S扇形COD＝eq \f(1,2)×eq \f(1,2)×2×2eq \r(3)＋eq \f(60π×22,360)＝eq \r(3)＋eq \f(2,3)π.
17. B 18. C 19. 3π－6 20. eq \f(2\r(3)π,3)
圆的周长
C＝①
(1)r为圆的半径；(2)n°为弧所对的圆心角的度数；
(3)l是扇形的弧长
扇形的弧长
l＝②
圆的面积
S＝③
扇形的面积
S＝④ ＝eq \f(1,2)lr
名称
图示
公式
展开图
圆锥
S底面圆＝πr2，
C底面圆＝2πr，
V圆锥＝eq \f(1,3)πr2h，
S侧面积＝πlr，
S表面积＝πlr＋πr2，r2＋h2＝l2
侧面展开图是扇形
圆柱
S圆柱侧＝⑤ ，
S圆柱全＝⑥ ＋2πr2，
V圆柱＝πr2h
侧面展开图为矩形