中考数学二轮专题复习《函数实际应用》解答题专项练习十（含答案）

中考数学二轮专题复习

《函数实际应用》解答题专项练习十

1.某苹果基地销售优质苹果，该基地对需要送货且购买量在2000 kg～5000 kg(含2000 kg和5000 kg)的客户有两种销售方案(客户只能选择其中一种方案)：

方案A：每千克5.8元，由基地免费送货.

方案B：每千克5元，客户需支付运费2000元.

(1)请分别写出按方案A，方案B购买这种苹果的应付款y(元)与购买量x(kg)之间的函数表达式；

(2)求购买量x在什么范围时，选用方案A比方案B付款少；

(3)某水果批发商计划用20000元，选用这两种方案中的一种，购买尽可能多的这种苹果，请写出他应选择哪种方案.

2.某药品研究所开发一种抗菌新药，经多年动物实验，首次用于临床人体试验，测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x小时之间函数关系如图所示(当4≤x≤10时，y与x成反比例).

(1)根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数关系式.

(2)问血液中药物浓度不低于4微克/毫升的持续时间多少小时？

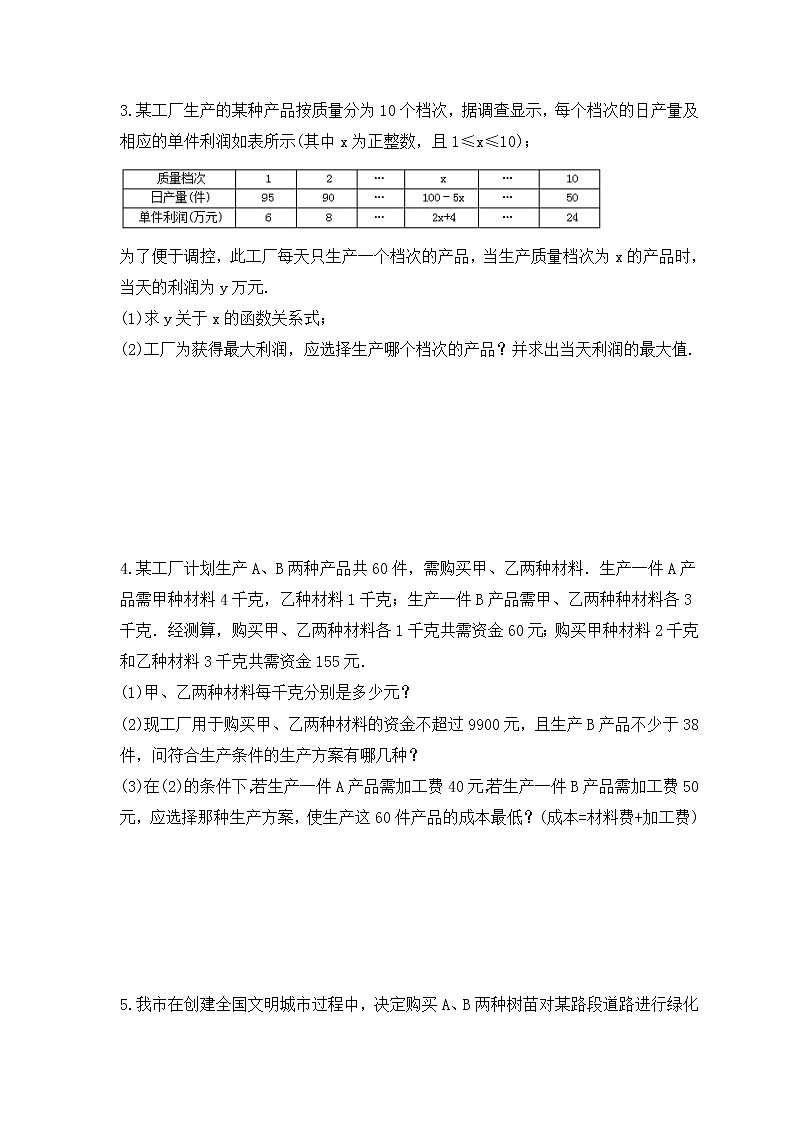
3.某工厂生产的某种产品按质量分为10个档次，据调查显示，每个档次的日产量及相应的单件利润如表所示(其中x为正整数，且1≤x≤10)；

为了便于调控，此工厂每天只生产一个档次的产品，当生产质量档次为x的产品时，当天的利润为y万元.

(1)求y关于x的函数关系式；

(2)工厂为获得最大利润，应选择生产哪个档次的产品？并求出当天利润的最大值.

4.某工厂计划生产A、B两种产品共60件，需购买甲、乙两种材料．生产一件A产品需甲种材料4千克，乙种材料1千克；生产一件B产品需甲、乙两种种材料各3千克．经测算，购买甲、乙两种材料各1千克共需资金60元；购买甲种材料2千克和乙种材料3千克共需资金155元．

(1)甲、乙两种材料每千克分别是多少元？

(2)现工厂用于购买甲、乙两种材料的资金不超过9900元，且生产B产品不少于38件，问符合生产条件的生产方案有哪几种？

(3)在(2)的条件下，若生产一件A产品需加工费40元，若生产一件B产品需加工费50元，应选择那种生产方案，使生产这60件产品的成本最低？(成本=材料费+加工费)

5.我市在创建全国文明城市过程中，决定购买A、B两种树苗对某路段道路进行绿化改造，已知购买A种树苗5棵，B种树苗10棵，需要1300元；购买A种树苗3棵，B种树苗5棵，需要710元.

(1)求购买A、B两种树苗每棵各需多少元？

(2)考虑到绿化效果和资金周转，购进A种树苗不能少于30棵，且用于购买这两种树苗的资金不能超过8650元，现需购进这两种树苗共100棵，则有哪几种购买方案？

(3)某包工队承包种植任务，若种好一棵A种树苗可获工钱25元，种好一棵B种树苗可获工钱15元，在第(2)问的各种购买方案中，种好这100棵树苗，哪一种购买方案所付的种植工钱最少？最少工钱是多少元？

6.利民商店经销甲、乙两种商品. 现有如下信息：
 

请根据以上信息，解答下列问题：

(1)甲、乙两种商品的进货单价各多少元?

(2)该商店平均每天卖出甲商品500件和乙商品300件.经调查发现，甲、乙两种商品零售单价分别每降0.1元，这两种商品每天可各多销售100件.为了使每天获取更大的利润，商店决定把甲、乙两种商品的零售单价都下降m元. 在不考虑其他因素的条件下，当m定为多少时，才能使商店每天销售甲、乙两种商品获取的利润最大？每天的最大利润是多少？

7.某水产养殖大户为了更好地发挥技术优势，一次性收购了20000 kg淡水鱼，计划养殖一段时间后再出售.已知每天放养的费用相同，放养10天的总成本为30.4万元；放养20天的总成本为30.8万元(总成本＝放养总费用＋收购成本).

(1)设每天的放养费用是a万元，收购成本为b万元，求a和b的值；

(2)设这批淡水鱼放养t天后的质量为m(kg)，销售单价为y元/kg.根据以往经验可知：

m与t的函数关系为m＝；y与t的函数关系如图所示.

①分别求出当0≤t≤50和50<t≤100时，y与t的函数关系式；

②设将这批淡水鱼放养t天后一次性出售所得利润为W元，求当t为何值时，W最大？并求出最大值.(利润＝销售总额－总成本)

0.参考答案

1.解：(1)方案A：函数表达式为：y=5.8x，

B：函数表达式为：y=5x＋2000；

(2)由题意得5.8x<5x＋2000，解不等式得x<2500，

∴当购买量x的取值范围为2000 kg≤x<2500 kg时，选用方案A比方案B付款少；

(3)他应选择方案B.

方案A中：y=20000时，x=20000÷5.8≈3448.3 kg；

方案B中：y=20000时，5x＋2000=20000，即x=3600 kg，

∴他应选择方案B.

2.解：(1)当0≤x≤4时，设直线解析式为：y=kx，

将(4，8)代入得：8=4k，解得：k=2，

故直线解析式为：y=2x，

当4≤x≤10时，设反比例函数解析式为：y=，

将(4，8)代入得：8=4a-1，解得：a=32，

故反比例函数解析式为：y=32x-1；

因此血液中药物浓度上升阶段的函数关系式为y=2x(0≤x≤4)，

下降阶段的函数关系式为y=32x-1(4≤x≤10).

(2)当y=4，则4=2x，解得：x=2，

当y=4，则4=32x-1，解得：x=8，

∵8﹣2=6(小时)，

∴血液中药物浓度不低于4微克/毫升的持续时间6小时.

3.解：(1)由题意，得y=(2x+4)，y=﹣10x2+180x+400(1≤x≤10的整数)；

答：y关于x的函数关系式为y=﹣10x2+180x+400；

(2)∵y=﹣10x2+180x+400，

∴y=﹣10(x﹣9)2+1210.

∵1≤x≤10的整数，

∴x=9时，y最大=1210.

答：工厂为获得最大利润，应选择生产9档次的产品，当天利润的最大值为1210万元.

4.解：(1)设甲材料每千克x元，乙材料每千克y元，
则x+y=60，2x+3y=155.，解得x=25，y=35.

所以甲材料每千克25元，乙材料每千克35元；
(2)设生产A产品m件，生产B产品(60-m)件，则生产这60件产品的材料费为
25×4m+35×1m+25×3(60-m)+35×3(60-m)=-45m+10800，
由题意：-45m+10800≤9900，解得m≥20，
又∵60-m≥38，解得m≤22，
∴20≤m≤22，
∴m的值为20，21，22，
共有三种方案：
①生产A产品20件，生产B产品40件；
②生产A产品21件，生产B产品39件；
③生产A产品22件，生产B产品38件．

(3)生产A产品21件，B产品39件成本最低．理由如下：

设生产成本为W元，则W与a的关系式为：

W=(25×4+35×1+40)(60﹣a)+(35×3+25×3+50)a=55a+10 500，

即W是a的一次函数，

∵k=55＞0

∴W随a增大而增大

∴当a=39时，总成本最低；

即生产A产品21件，B产品39件成本最低．

5.解：(1)设购买A种树苗每棵需要x元，B种树苗每棵需要y元，

由题意得：，解得：.

答：购买A种树苗每棵需要120元，B种树苗每棵需要70元.

(2)设购买A种树苗m棵，则购买B种树苗(100﹣m)棵，

根据已知，得，解得：30≤m≤33.

故有四种购买方案：

方案1、购买A种树苗30棵，B种树苗70棵；

方案2、购买A种树苗31棵，B种树苗69棵；

方案3、购买A种树苗32棵，B种树苗68棵；

方案4、购买A种树苗33棵，B种树苗67棵.

(3)设种植工钱为W，由已知得：

W＝25m＋15(100﹣m)＝10m＋1500，

∵10＞0，W随x的增大而增大，

∴当m＝30时，W最小，最小值为1800元.

故购买A种树苗30棵、B种树苗70棵时所付的种植工钱最少，最少工钱是1800元.

6.解：(1)设甲商品的进货单价是x元，乙商品的进货单价是y元.据题意，得解得 

答：甲商品的进货单价是2元，乙商品的进货单价是3元.

(2)设商店每天销售甲、乙两种商品获取的利润为s元，则

s=(1﹣m)(500+100×)+(5﹣3﹣m)(300+100×)

即s=﹣2000m2+2200m+1100=﹣2000(m﹣0.55)2+1705.

∴当m=0.55时，s有最大值，最大值为1705. 

答：当m定为0.55时，才能使商店每天销售甲、乙两种商品获取的利润最大，每天的最大利润是1705元.

7.解：(1)由题意得解得

即a的值为0.04，b的值为30

(2)①当0≤t≤50时，设y与x的函数关系式为y＝k1t＋n1,

把点(0，15)和(50，25)的坐标分别代入y＝k1t＋n1,

解得∴y与t的函数关系式为y＝t＋15；

当50<t≤100时，设y与t的函数关系式为y＝k2t＋n2，

把点(50，25)和(100，20)的坐标分别代入y＝k2t＋n2，

解得∴y与t的函数关系式为y＝－t＋30

②由题意得，当0≤t≤50时，W＝20000(t＋15)－(400t＋300000)＝3600t，

∵3600>0，

∴当t＝50时，W最大值＝180000(元)；

当50<t≤100时，W＝(100t＋15000)(－t＋30)－(400t＋300000)

＝－10t2＋1100t＋150000＝－10(t－55)2＋180250，

∵－10<0，

∴当t＝55时，W最大值＝180250(元)；

综上所述，当t为55时，W最大，最大值为180250元