




冀教版九年级下册30.2 二次函数的图像和性质优秀课件ppt
展开二次函数 y=ax 2,y=ax 2+k 有何位置关系?
二次函数 y=ax 2向上平移k (k>0)个单位就得到二次函数 y=ax 2+k 的图象是什么?
二次函数 y=ax 2向下平移k (k>0)个单位就得到二次函数 y=ax 2-k 的图象是什么?
前面我们学习了y=ax 2,y=ax 2+k 型二次函数的图象和性质,今天我们将学习另一种类型的二次函数的图象和性质.
二次函数y=a(x-h)2的图象
二次函数y = (x-1)2的图象与二次函数 y = x 2的图象有什么关系? 类似地,你能发现二次函数y = (x+1)2的图象与二次函数y = (x-1)2的图象有什么关系吗?
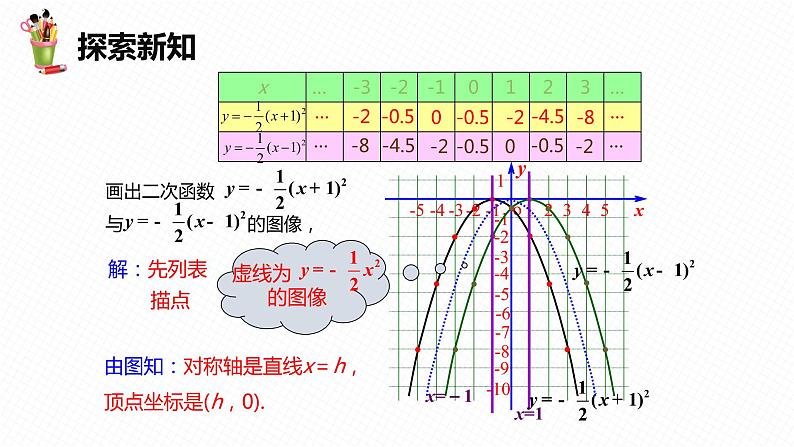
画出二次函数 与 的图像,
由图知:对称轴是直线x=h,顶点坐标是(h,0).
虚线为 的图像
从形状上看,二次函数 与的图像与二次函数 的图像的形状和位置有什么关系?
形状相同,位置不同.
1 抛物线 y=-5(x-2)2的顶点坐标是( ) A.(-2,0) B.(2,0) C.(0,-2) D.(0,2)
在下列二次函数中,其图象的对称轴为直线x=-2的是( ) A.y=(x+2)2 B.y=2x 2-2 C.y=-2x 2-2 D.y=2(x-2)2
对于抛物线 y=2(x-1)2,下列说法正确的有( )①开口向上;②顶点为(0,-1);③对称轴为直线x=1;④与x 轴的交点坐标为(1,0).A.1个 B.2个 C.3个 D.4个
抛物线 的开口方向、对称轴、顶点坐标、增减性和最值?
(2)抛物线 的开口方向、对称轴、顶点坐标、 增减性和最值?
二次函数y=a(x-h)2的性质
根据图象得出二次函数 y=a (x-h)2的性质如下表:
负半轴上,所以不与x 轴相交;函数y= x 2-1与y= (x-1)2的二次项系数相同,所以抛物线的形状相同, 因为对称轴和顶点的位置不同,所以抛物线的位置不同;抛物线y= 的顶点坐标为 ;抛物线y= 的对称轴是直线x=- .
导引:抛物线y=- x 2-1的开口向下,顶点在y 轴的
本题运用了性质判断法和数形结合思想,运用二次函数的性质,画出图象进行判断.
在同一直角坐标系中,一次函数 y=ax+c 和二次函数 y=a (x+c )2的图象可能是( )
2 关于二次函数y=-2(x+3)2,下列说法正确的是( ) A.其图象的开口向上 B.其图象的对称轴是直线x=3 C.其图象的顶点坐标是(0,3) D.当x>-3时,y 随x 的增大而减小
已知抛物线y=-(x+1)2上的两点A (x1,y1),B (x2,y2), 如果x1<x2<-1,那么下列结论成立的是( ) A.y1<y2<0 B.0<y1<y2 C.0<y2<y1 D.y2<y1<0
二次函数y =a(x-h)2与y =ax 2之间的关系
前面已画出了抛物线y =- (x+1)2,y =- (x-1)2,在此坐标系中画出抛物线y =- x 2 (见图中虚线部分), 观察抛物线y =- (x+1)2,y =- (x-1)2与抛物线y =- x 2有什么关系?
抛物线 与抛物线 有什么关系?
对称轴:y 轴即直线:x =0
在同一坐标系中作出下列二次函数:
例2 二次函数y =- (x-5)2的图象可有抛物线 y =- x 2 沿___轴向___平移___个单位得到,它的开口向___, 顶点坐标是_________,对称轴是_________.当x =___时, y 有最____值.当x___5时,y 随x 的增大而增大;当 x___5时,y 随x 的增大而减小.
y =- (x-5)2的图象与抛物线y =- x 2的形状相同,但位置不同,y =- (x-5)2的图象由抛物线y =- x 2向右平移5个单位得到.
把抛物线 y =x 2平移得到抛物线 y =(x+2)2,则这个平移过程正确的是( ) A.向左平移2个单位长度 B.向右平移2个单位长度 C.向上平移2个单位长度 D.向下平移2个单位长度
对于任何实数h,抛物线 y=-x 2与抛物线 y =-(x-h)2的相同点是( ) A.形状与开口方向相同 B.对称轴相同 C.顶点相同 D.都有最低点
将函数 y=x 2的图象用下列方法平移后,所得的图象不经过点A(1,4)的方法是( )A.向左平移1个单位长度B.向右平移3个单位长度C.向上平移3个单位长度D.向下平移1个单位长度
对于二次函数 y=3x 2+1和 y=3(x-1)2,以下说法:①它们的图象都是开口向上;②它们图象的对称轴都是 y 轴,顶点坐标都是(0,0);③当x >0时,它们的函数值 y 都是随着x 的增大而增大;④它们图象的开口的大小是一样的.其中正确的说法有( )A.1个 B.2个 C.3个 D.4个
易错点:函数y=ax 2+c 与y=a (x-h)2的图象与性质区别不清
二次函数 y=3x 2+1的图象开口向上,对称轴是 y 轴,顶点坐标是(0,1),当x >0时,y 随x 的增大而增大;二次函数y=3(x-1)2的图象开口向上,对称轴是直线x=1,顶点坐标是(1,0),当x >1时,y 随x 的增大而增大;二次函数 y=3x 2+1和y=3(x-1)2的图象的开口大小一样.因此正确的说法有2个:①④.故选B.
已知二次函数y=-2(x+m)2,当x<-3时,y 随x 的增大而增大;当x>-3时,y 随x 的增大而减小,则当x=1时,y 的值为( )A.-12 B.12 C.32 D.-32
平行于x 轴的直线与抛物线y=a (x-2)2的一个交点坐标为(-1,2),则另一个交点坐标为( )A.(1,2) B.(1,-2)C.(5,2) D.(-1,4)
3 已知抛物线 y=a (x-h)2的对称轴为x=-2,且过点(1,-3). (1)求抛物线的表达式. (2)画出函数的图像. (3)从图像上观察,当x 取何值时,y 随x 的增大而增大? 当x 取何值时,函数有最大值(或最小值)?
(1)由题意知h=-2.将点(1,-3)的坐标代入y=a (x+2)2 得a=- ,所以抛物线的表达式为y=- (x+2)2.(2)图像略.(3)当x<-2时,y 随x 的增大而增大;当x= -2时,函数有最大值.
4 已知抛物线 y=a (x-h)2向右平移3个单位长度后得 到抛物线 y= x 2. (1)求a,h 的值; (2)写出抛物线 y=a (x-h)2的对称轴及顶点坐标.
(1)a= ,h=-3.(2)抛物线 y= (x+3)2的对称轴为x=-3,顶点坐 标为(-3,0).
如图,将抛物线 y=x 2向右平移a 个单位长度后,顶点为A, 与y 轴交于点B,且△AOB 为等腰直角三角形. (1)求a 的值. (2)在图中的抛物线上是否存在点C,使△ABC 为等腰 直角三角形?若存在,直接写出点C 的坐标,并求 S△ABC;若不存在,请说明理由.
(1)依题意将抛物线 y=x 2平移后为抛物线y=(x-a)2,即 y=x 2-2ax+a 2. 又OA=OB,点A 的坐标为(a,0),点B 的坐标为(0,a 2), ∴a 2=a. ∵a ≠ 0,∴a=1.(2)存在.由(1)可得点 A 的坐标为(1,0),点B 的坐标为 (0,1),由抛物线的对称性可知,C 点的坐标为(2, 1),此时可求AB=AC,∠BAC=90°. 又易知AB=AC= , ∴S△ABC= AB ·AC= × × =1.
6 如图,已知二次函数 y =(x+2)2的图像与x 轴交于点A, 与y 轴交于点B. (1)写出点A,点B 的坐标. (2)求S△AOB. (3)求出抛物线的对称轴. (4)在对称轴上是否存在一点P,使以P,A,O,B 为顶 点的四边形为平行四边形?若存在,求出P 点的坐标; 若不存在,请说明理由.
(1)在 y=(x+2)2中,令y=0,得x=-2;令x=0,得y =4. ∴点A,点B 的坐标分别为(-2,0),(0,4).(2)∵点A,点B 的坐标分别为(-2,0),(0,4), ∴OA=2,OB=4. ∴S△AOB= OA·OB= ×2×4=4.(3)抛物线的对称轴为x=-2.(4)存在.①以OA 和OB 为邻边可作平行四边形P1AOB, 易求得P1(-2,4);②以AB 和OB 为邻边可作平行 四边形P2ABO,易求得P2(-2,-4).
二次函数 y=a (x-h)2的图象和性质
y=a (x-h)2图象a>0时,开口向上,最低点是顶点;a<0时,开口向下,最高点是顶点;对称轴是直线x=h,顶点坐标是(h,0).
向右平移h 个单位(h>0)
向左平移h 个单位(h>0)
冀教版九年级下册30.2 二次函数的图像和性质优秀ppt课件: 这是一份冀教版九年级下册30.2 二次函数的图像和性质优秀ppt课件,共42页。PPT课件主要包含了课前导入,新课精讲,学以致用,课堂小结,情景导入,探索新知,典题精讲,易错提醒,小试牛刀等内容,欢迎下载使用。
数学九年级下册30.2 二次函数的图像和性质一等奖ppt课件: 这是一份数学九年级下册30.2 二次函数的图像和性质一等奖ppt课件,共41页。PPT课件主要包含了课前导入,新课精讲,学以致用,课堂小结,情景导入,探索新知,典题精讲,易错提醒,小试牛刀等内容,欢迎下载使用。
冀教版九年级下册30.2 二次函数的图像和性质获奖ppt课件: 这是一份冀教版九年级下册30.2 二次函数的图像和性质获奖ppt课件,共42页。PPT课件主要包含了课前导入,新课精讲,学以致用,课堂小结,情景导入,探索新知,典题精讲,函数的上下移动,易错提醒,小试牛刀等内容,欢迎下载使用。













