2022-2023 数学浙教版新中考精讲精练 考点11一次函数的图象与性质

考点11一次函数的图象与性质

考点总结

1．有关概念：

一般地，函数y＝kx＋b(k，b都是常数，且k≠0)叫做一次函数．当b＝0时，一次函数y＝kx＋b就成为y＝kx(k为常数，k≠0)，叫做正比例函数，常数k叫做比例系数．一次函数的表达式通常用待定系数法来求．

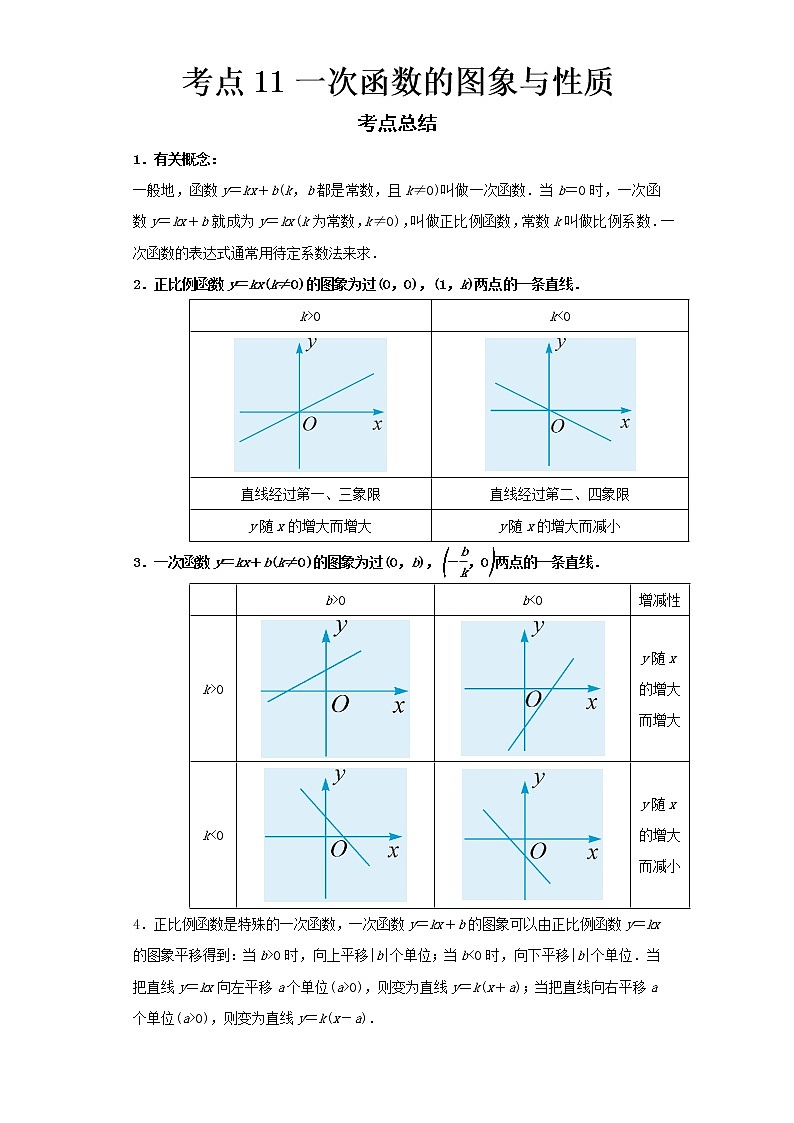
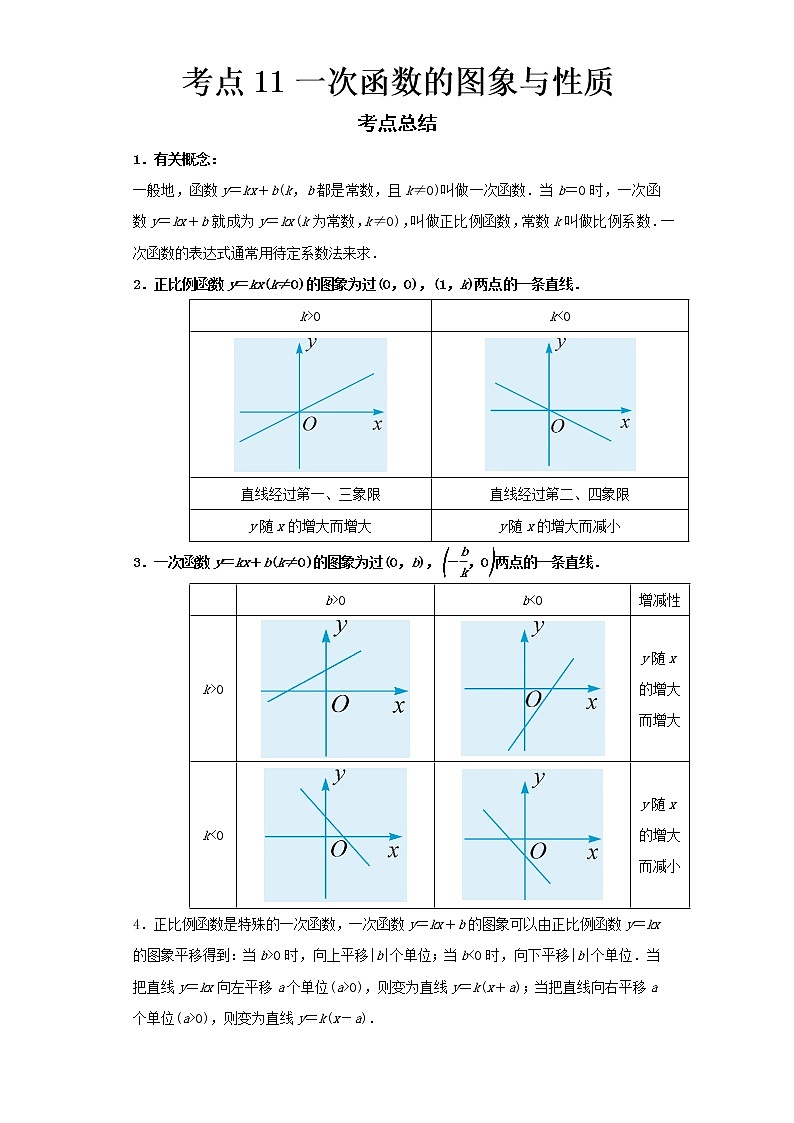
2．正比例函数y＝kx(k≠0)的图象为过(0，0)，(1，k)两点的一条直线．

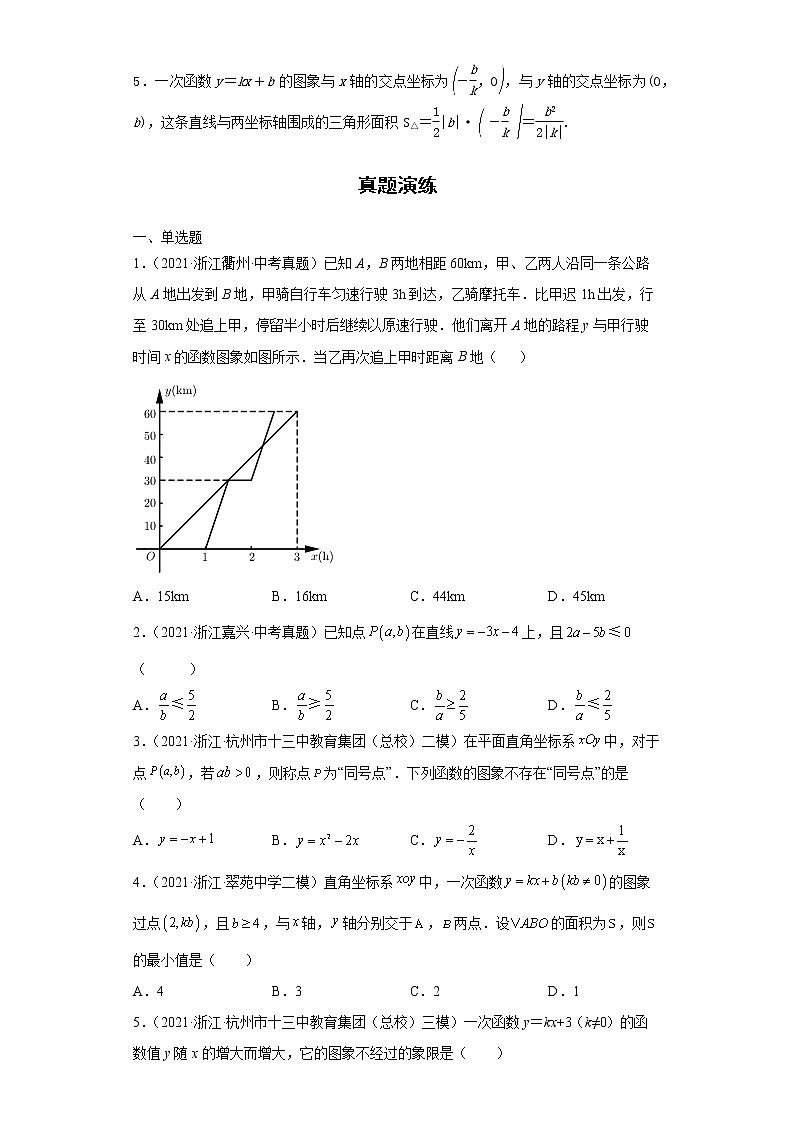
3．一次函数y＝kx＋b(k≠0)的图象为过(0，b)，两点的一条直线．

4．正比例函数是特殊的一次函数，一次函数y＝kx＋b的图象可以由正比例函数y＝kx的图象平移得到：当b>0时，向上平移|b|个单位；当b<0时，向下平移|b|个单位．当把直线y＝kx向左平移a个单位(a>0)，则变为直线y＝k(x＋a)；当把直线向右平移a个单位(a>0)，则变为直线y＝k(x－a)．

5．一次函数y＝kx＋b的图象与x轴的交点坐标为，与y轴的交点坐标为(0，b)，这条直线与两坐标轴围成的三角形面积S△＝|b|·＝.

真题演练

一、单选题

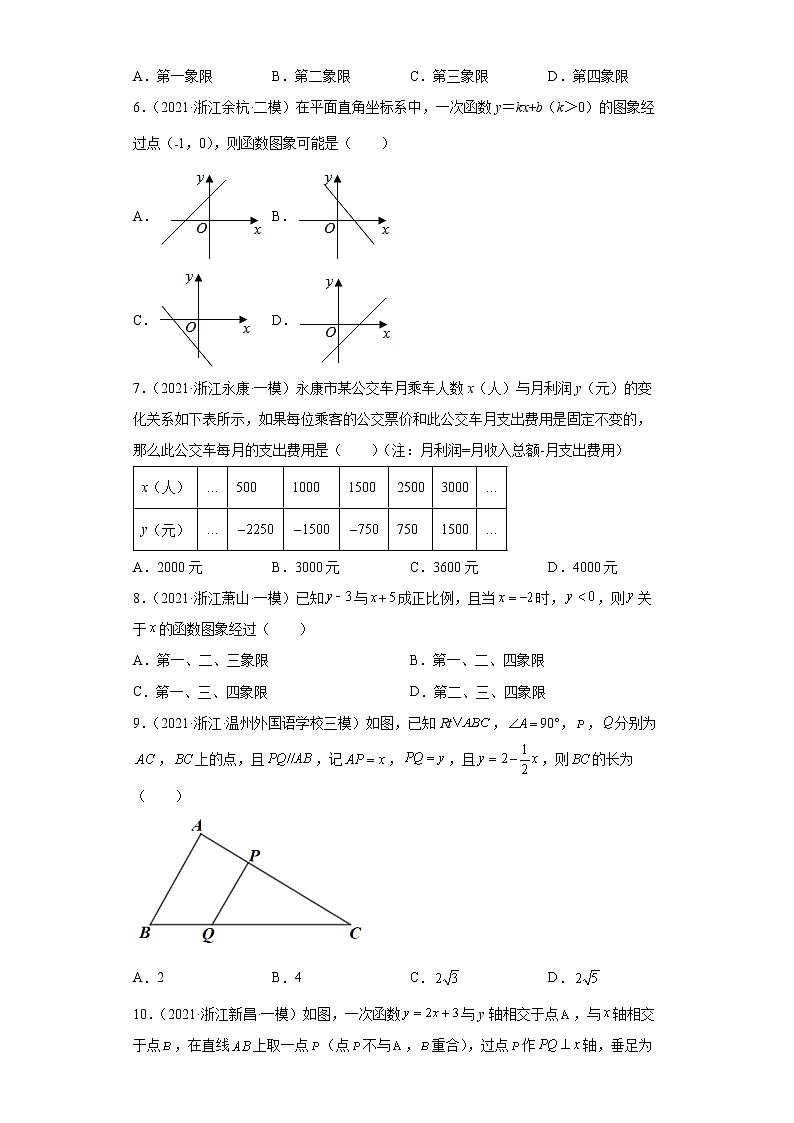
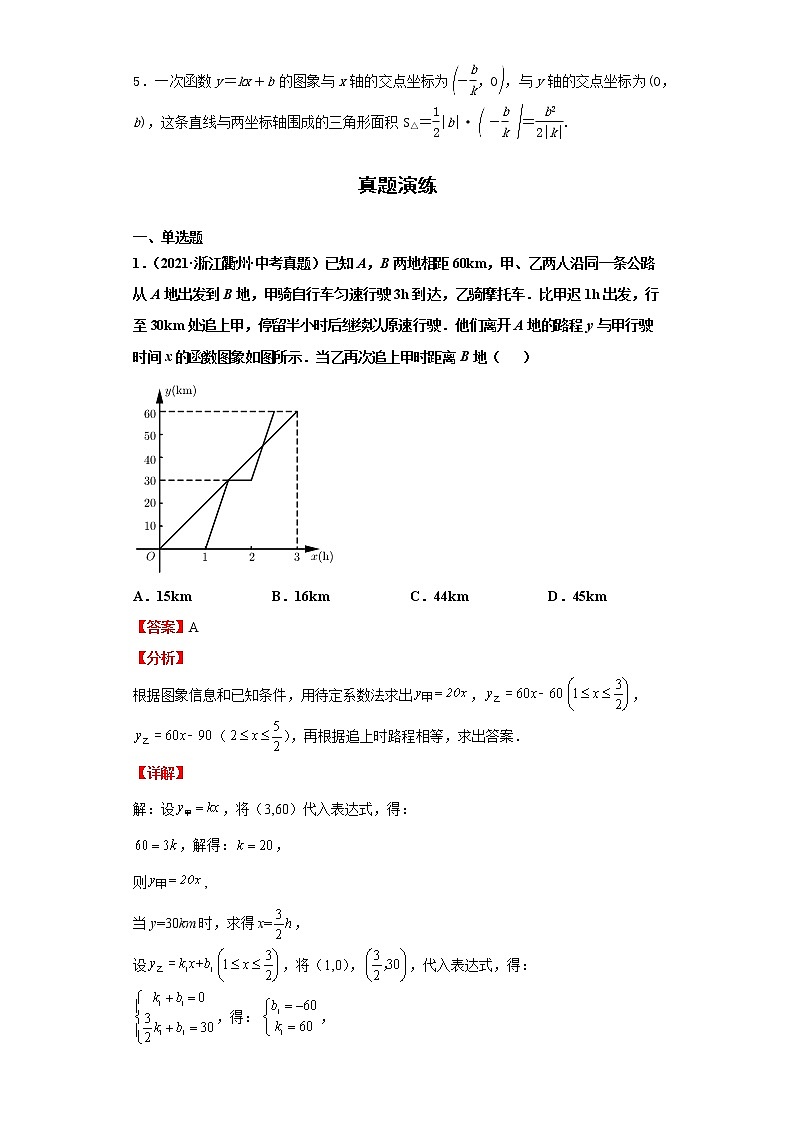
1．（2021·浙江衢州·中考真题）已知A，B两地相距60km，甲、乙两人沿同一条公路从A地出发到B地，甲骑自行车匀速行驶3h到达，乙骑摩托车．比甲迟1h出发，行至30km处追上甲，停留半小时后继续以原速行驶．他们离开A地的路程y与甲行驶时间x的函数图象如图所示．当乙再次追上甲时距离B地（   ）

A．15km B．16km C．44km D．45km

【答案】A

【分析】

根据图象信息和已知条件，用待定系数法求出，，（），再根据追上时路程相等，求出答案．

【详解】

解：设，将（3,60）代入表达式，得：

，解得：，

则,

当y=30km时，求得x=，

设，将（1,0），，代入表达式，得：

，得：，

∴，

∴，，

∵乙在途中休息了半小时，到达B地时用半小时，

∴当时，设，将（2,30），代入表达式，得到：

，得：，

∴（），

则当时，，

解得：，

∴,

∴当乙再次追上甲时距离A地45km

所以乙再次追上甲时距离地

故选：A．

2．（2021·浙江嘉兴·中考真题）已知点在直线上，且（      ）

A． B． C． D．

【答案】D

【分析】

根据点在直线上，且，先算出的范围，再对不等式变形整理时，需要注意不等号方向的变化．

【详解】

解：点在直线上，

，

将上式代入中，

得：，

解得：，

由，得：，

（两边同时乘上一个负数，不等号的方向要发生改变），

故选：D．

3．（2021·浙江·杭州市十三中教育集团（总校）二模）在平面直角坐标系中，对于点，若，则称点为“同号点”．下列函数的图象不存在“同号点”的是（    ）

A． B． C． D．

【答案】C

【分析】

根据题意可知图象经过第一和第三象限的函数都是满足条件的，由此分析判断即可．

【详解】

解：由题意，图象经过第一和第三象限的函数都是满足条件的，
函数的图象在二四象限，不满足条件，
故选：C．

4．（2021·浙江·翠苑中学二模）直角坐标系中，一次函数的图象过点，且，与轴，轴分别交于，两点．设的面积为，则的最小值是（    ）

A．4 B．3 C．2 D．1

【答案】A

【分析】

首先将（2，kb）点代入一次函数解析式，求出k与b的关系式，再求出一次函数y=kx+b（kb≠0）的图象与x轴、y轴分别交于A、B两点坐标，表示出△ABO的面积S，再根据b≥4，去掉绝对值，利用二次函数最值求法，可求出S的最小值．

【详解】

解：一次函数的图象过点，代入一次函数解析式得：

，

，

，

，

一次函数的图象与轴、轴分别交于、两点，

点坐标为：，，点的坐标为：，

的面积为，

；

若，，

，

的最小值为：．

故选：A．

5．（2021·浙江·杭州市十三中教育集团（总校）三模）一次函数y＝kx+3（k≠0）的函数值y随x的增大而增大，它的图象不经过的象限是（　　）

A．第一象限 B．第二象限 C．第三象限 D．第四象限

【答案】D

【分析】

根据一次函数的性质可直接进行求解．

【详解】

解：∵一次函数y＝kx+3（k≠0）的函数值y随x的增大而增大，

∴k＞0，

∴该函数经过第一、二、三象限，不经过第四象限，

故选：D．

6．（2021·浙江余杭·二模）在平面直角坐标系中，一次函数y＝kx+b（k＞0）的图象经过点（﹣1，0），则函数图象可能是（　　）

A． B． C． D．

【答案】A

【分析】

先由函数y＝kx+b（k＞0）的图象过点（﹣1，0），可判断经过x轴的负半轴，由k＞0可判断图象经过第一、二、三象限，综合分析即可．

【详解】

∵一次函数y＝kx+b（k＞0）的图象经过点（﹣1，0），

∴一次函数y＝kx+b（k＞0）的图象经过x轴的负半轴．

∵k＞0，

∴y随x的增大而增大．

∴一次函数y＝kx+b（k＞0）的图象经过第一、二、三象限．

∴函数图象可能是：A．

故选：A．

7．（2021·浙江永康·一模）永康市某公交车月乘车人数x（人）与月利润y（元）的变化关系如下表所示，如果每位乘客的公交票价和此公交车月支出费用是固定不变的，那么此公交车每月的支出费用是（    ）（注：月利润=月收入总额-月支出费用）

A．2000元 B．3000元 C．3600元 D．4000元

【答案】B

【分析】

根据表格可知乘车人数x（人）与月利润y（元）的一次函数变化关系，设每位乘客的公交票价为元，公交车每月的支出费用为b元，可得，把表格数据代入两组求出b即可解答．

【详解】

解： 设每位乘客的公交票价为元，公交车每月的支出费用为b元，则，

依题意得： ，

解得：，

即此公交车每月的支出费用是3000元；

 故选B．

8．（2021·浙江萧山·一模）已知与成正比例，且当时，，则关于的函数图象经过（    ）

A．第一、二、三象限 B．第一、二、四象限

C．第一、三、四象限 D．第二、三、四象限

【答案】D

【分析】

由y-3与x+5成正比例，可设y-3=k（x+5），整理得：y=kx+5k+3．把x=-2代入得不等式，可解得k＜-1，再判断5k+3的符号即可．

【详解】

解：∵y-3与x+5成正比例，

∴设y-3=k（x+5），整理得：y=kx+5k+3．

当x=-2时，y＜0，

即-2k+5k+3＜0，整理得3k+3＜0，

解得：k＜-1．

∵k＜-1，

∴5k+3＜-2，

∴y=kx+5k+3的图象经过第二、三、四象限．

故选：D．

9．（2021·浙江·温州外国语学校三模）如图，已知Rt，90°，，分别为，上的点，且，记，，且，则的长为（    ）

A．2 B．4 C． D．

【答案】D

【分析】

根据题意可当，则有，即，此时点P、Q与点C重合，当时，则有，此时点P与点A重合，点Q与AB重合，进而可得AB=2，AC=4，然后根据勾股定理可求解．

【详解】

解：∵，，，且，

∴当，则有，即，

∴点P、Q与点C重合，则AC=4，

当时，则有，

∴点P与点A重合，点Q与AB重合，即AB=2，

∴在Rt中，；

故选D．

10．（2021·浙江新昌·一模）如图，一次函数与y轴相交于点，与轴相交于点，在直线上取一点（点不与，重合），过点作轴，垂足为点，连结，若的面积恰好为，则满足条件的点有（    ）

A．1个 B．2个 C．3个 D．4个

【答案】C

【分析】

设p(t，2t+3)，则Q(t，0)，分三种情况分析解答：当p在第一象限时，当p在第二象限时，当p在第三象限时．

【详解】

解：一次函数，令x=0，则y=3；令y=0，则0=2x+3，解得x=，

∴A(0，3)，B(，0)，

设p(t，2t+3)，则Q(t，0)，

当p在第一象限时，

，

∴，解得t=（负值舍去），

∴2t+3=，

∴P(，)；

当p在第二象限时，

∴=，解得t= -，

∴2t+3=，

∴P(-，)；

当p在第三象限时，

，

∴=，解得t=（正值舍去），

∴2t+3=，

∴P(，)；

综上所述，P点的坐标共3个，

故选C．

二、填空题

11．（2021·浙江·温州绣山中学三模）已知 y是关于x的一次函数，下表列出了部分对应值，则a的值为____．

【答案】

【分析】

把代入一次函数中，求得一次函数解析式，然后把代入一次函数解析式，即可求出a的值．

【详解】

解：∵y是关于x的一次函数，

∴设一次函数解析式为：，

把代入中得：

，解得：，

∴一次函数的解析式为：，

把代入得：，

故答案为：．

12．（2021·浙江拱墅·二模）A城有种农机30台，B城有该农机40台，现要将这些农机全部运往C，D两乡，调运任务承包给某运输公司．已知C乡需要农机34台，D乡需要农机36台，从A城往C，D两乡运送农机的费用分别为250元/台和200元/台，从B城往C，D两乡运送农机的费用分别为150元/台和240元/台．设A城运往C乡该农机x台，运送全部农机的总费用为W元，则W关于x的函数关系式为_______________．

【答案】

【分析】

因为A城运往C乡x台农机，则A城运往D乡（30﹣x）台农机，B城运往C乡（34﹣x）台农机，B城运往D乡[40﹣（34﹣x）]台农机，就可以得到关系式．

【详解】

解：由题意得：因为A城运往C乡x台农机，则A城运往D乡（30﹣x）台农机，B城运往C乡（34﹣x）台农机，B城运往D乡[40﹣（34﹣x）]台农机

W＝250x+200（30﹣x）+150（34﹣x）+240[40﹣（34﹣x）]

＝140x+12540，

故答案为：W＝140x+12540．

13．（2021·浙江桐乡·一模）如图，已知一次函数的图像分别与轴，轴相交于点，，是直线上一点，当时，点的坐标是______．

【答案】或

【分析】

根据题意在函数图象上做出可能存在的点的位置，做出OD⊥AB于点D，利用勾股定理结合三角函数求出相应的，再设出点C坐标求解即可．

【详解】

与轴，轴相交于点，，

∴A（5，0），B（0，），

∴ ，

，

∴，

如图：作OD⊥AB于点D，

∴，

∴ ，

∵，

∴，

∴，

又∵点C在直线上，

∴设C（t，），

代入，

解得：t=3或-1，

∴点C坐标为或．

故答案为：或

14．（2021·浙江嵊州·模拟预测）如图，在平面直角坐标系xOy中，一次函数y＝kx+b的图象与x轴，y轴分别交于点A和点B，与反比例函数y＝（m＞0）的图象交于点C（2，4），B为线段AC的中点，若点D为线段AC上的一个动点，过点D作DE∥x轴，交反比例函数图象于点E，连接OD，OE，则△ODE面积的最大值为___．

【答案】．

【分析】

一次函数y＝kx+b的图象与x轴，y轴分别交于点A和点B，用k、b的值表示点A和点B的坐标，根据B为线段AC的中点，求得点A和点B的坐标及k、b的值，可得一次函数解析式，根据点C坐标可得反比例函数解析式，延长ED交y轴于点F，设点E纵坐标为a，可得点E和点D坐标，根据S△ODE= S△OFE- S△OFD可求得关于a的二次函数，利用二次函数的性质即可得到△ODE面积的最大值．

【详解】

解：对于一次函数y＝kx+b，

当x=0时，y=b，

∴B(0，b)，

当y=0时，kx+b=0，

解得x=，

∴A(,0)，

∵点C（2，4），B为线段AC的中点，

∴点B纵坐标为2，

∴B(0，2)，

即b=2，

∵点A与点C关于点B对称，

∴点A横坐标为-2，

∴A(-2,0)，

即=-2，

∴k=1，

∴一次函数解析式为y=x+2，

∵反比例函数y＝（m＞0）的图象过点C(2，4)，

∴将点C(2，4)代入，得m=8，

∴反比例函数y＝，

延长ED交y轴于点F，

设点E纵坐标为a，把y=a代入y＝，得x=，

则E(,a)，

把y=a代入y=x+2，得x+2=a，

∴x=a-2，

∴D(a-2,a)，

∴S△ODE= S△OFE- S△OFD=，

∵EF=，DF=a-2，OF=a，

∴S△ODE==，

∴当a=1时，S△ODE有最大值，最大值为．

故答案为．

15．（2021·浙江·温州绣山中学二模）如图，一次函数的图象与x轴，y轴分别交于A，B两点．C是线段AB上一点，于点D，于点E，，则点C的坐标为___________．

【答案】

【分析】

根据题意易得四边形CDOE是矩形，设CD=x，则OD=2x，进而可得，然后代入一次函数解析式进行求解即可．

【详解】

解：∵，，

∴，

∵∠AOB=90°，

∴四边形CDOE是矩形，

∴OE=CD，

∵，

∴，

设CD=x，则OD=2x，

∴点，

代入一次函数得：，解得：，

∴点C的坐标为；

故答案为．

三、解答题

16．（2021·浙江衢州·中考真题）如图1，点C是半圆O的直径AB上一动点（不包括端点），，过点C作交半圆于点D，连结AD，过点C作交半圆于点E，连结EB．牛牛想探究在点C运动过程中EC与EB的大小关系．他根据学习函数的经验，记，，．请你一起参与探究函数、随自变量x变化的规律．

通过几何画板取点、画图、测量，得出如下几组对应值，并在图2中描出了以各对对应值为坐标的点，画出了不完整图象．

（1）当时，＝          ．

（2）在图2中画出函数的图象，并结合图象判断函数值与的大小关系．

（3）由（2）知“AC取某值时，有”．如图3，牛牛连结了OE，尝试通过计算EC，EB的长来验证这一结论，请你完成计算过程．

【答案】（1）3；（2）当x约等于2时，y1=y2；当0<x<2时，y1<y2；当 x>2时，y1>y2；（3）见解析
【分析】

（1）根据圆的直径为6，半径为3可求；

（2）按自变量由小到大的顺序描点并用平滑曲线连接即可得到所画图象，两图象有交点，过此交点作x轴的垂线，垂足表示的数即为自变量x的值，找到此值，即可比较两函数值的大小；

（3）在（2）的基础上，取AC=2，借助于勾股定理、相似三角形等知识，分别计算EC和EB，即可得出结论的正确性．

【详解】

解（1）当x=3时，动点C与圆心O重合，此时，y1=OE=3．

故答案为：3

（2）函数y2的图象如图2所示，过两图象的交点M作x轴的垂线，垂足为N，则垂足N表示的数．

∴从图象可以看出：

当时，；

当0<x<2时，；

当x>2时，．

（3）如图3，连结OD，过点E作于点H．

由（2）的初步判断，当时，，即EC=EB．

不妨取AC=x=2，此时，，．

，

∴在中，

．

设，则，．

∵AD∥CE，

∴∠DAC=∠ECO．

又，

∴．

∴．

∴．

∴．

两边平方并整理得，．

解得，（不合题意，舍去）．

∴OH=m=1．

∴HC=OH+OC=1+1=2，．

∴．

又∵HB=OB-OH=3-1=2，

∴．

∴EC=EB．

∴通过以上计算可知，当取AC=2时，（2）中的结论EC=EB成立．

17．（2021·浙江嘉兴·中考真题）根据数学家凯勒的“百米赛跑数学模型”，前30米称为“加速期”，30米～80米为“中途期”（m/s）与路程之间的观测数据

（1）是关于的函数吗？为什么？

（2）“加速期”结束时，小斌的速度为多少？

（3）根据如图提供的信息，给小斌提一条训练建议．

【答案】（1）是的函数，理由见解析；（2）“加速期”结束时，小斌的速度为10.4m/s；（3）答案不唯一．例如：根据图象信息，小斌在80米左右时速度下降明显，建议增加耐力训练，提高成绩．

【分析】

（1）根据函数的概念进行解答；

（2）通过识图读取相关信息；

（3）根据图像信息进行解答．

【详解】

解：（1）是的函数．

在这个变化过程中，对于的每一个确定的值，都有唯一确定的值与之对应．

（2）“加速期”结束时，小斌的速度为10.4m/s．

（3）答案不唯一．例如：根据图象信息，小斌在80米左右时速度下降明显，建议增加耐力训练，提高成绩．

18．（2021·浙江丽水·中考真题）李师傅将容量为60升的货车油箱加满后，从工厂出发运送一批物资到某地．行驶过程中，货车离目的地的路程s（千米）与行驶时间t（小时）的关系如图所示（中途休息、加油的时间不计．当油箱中剩余油量为10升时，货车会自动显示加油提醒．设货车平均耗油量为0.1升/千米，请根据图象解答下列问题：

（1）直接写出工厂离目的地的路程；

（2）求s关于t的函数表达式；

（3）当货车显示加油提醒后，问行驶时间t在怎样的范围内货车应进站加油？

【答案】（1）工厂离目的地的路程为880千米；（2）；（3）．

【分析】

（1）根据图象直接得出结论即可；

（2）根据图象，利用待定系数法求解函数表达式即可；再求出油量为

（3）分别求出余油量为10升和0升时行驶的路程，根据函数表达式求出此时的t值，即可求得t的范围．

【详解】

解：（1）由图象，得时，，

答：工厂离目的地的路程为880千米．

（2）设，将和分别代入表达式，

得，解得，

∴s关于t的函数表达式为．

（3）当油箱中剩余油量为10升时，（千米），

，解得（小时）．

当油箱中剩余油量为0升时，（千米），

，解得（小时）．

随t的增大而减小，

的取值范围是．