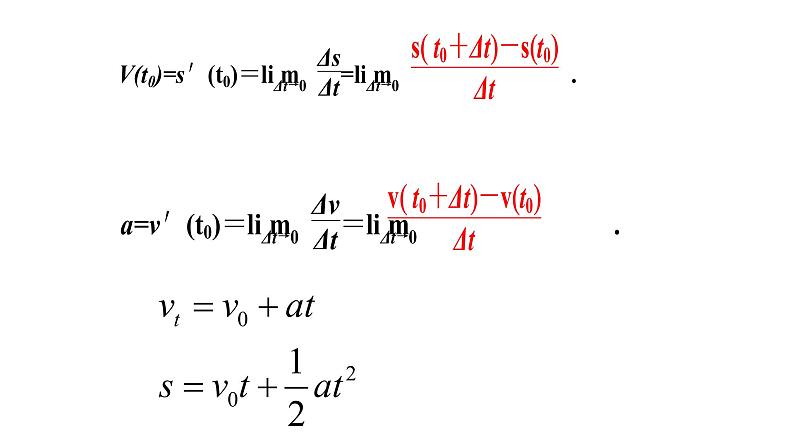
导数问题研究策略——清华附中高考数学研究课件PPT

这是一份导数问题研究策略——清华附中高考数学研究课件PPT，共60页。PPT课件主要包含了微积分基本思想，一导数概念，几种常见的导数，在词语，概念判断，导数问题解题策略，4分类讨论，5问题转化，4画出示意图，构造函数等内容，欢迎下载使用。

1.牛顿在1671年写了《流数法和无穷级数》，这本书直到1736年才出版，德国的莱布尼茨1684年，他发表了现在世界上认为是最早的微积分文献.2.极限思想、化曲为直、分割逼近。
“一尺之棰，日取其半，万世不竭”刘徽在他的割圆术中提到“割之弥细，所失弥小，割之又割，以至于不可割，则与圆周和体而无所失矣。”
如果没有微积分，科学将倒退200年。
切线方程为 ．
4.四则运算法则及复合函数求导
解决此类问题需要对导数等于0的地方进行检验.
一. 六个主要题型——核心是单调区间！
1.求曲线切线方程； 2.讨论函数单调区间； 3.讨论函数极值、最值； 4.讨论函数零点个数（或方程根的个数）； 5.不等式恒成立、或存在型问题； 6.证明不等式.（或一条曲线在另一条曲线上方，与不等式恒成立是相似问题）
（1）化归：讨论极值、最值、零点个数、 恒成立或存在性问题、证明不等式都 可以化归为讨论函数单调区间问题。（2）建构：“分析问题，构建函数， 研究函数，解决问题”（3）数形结合：直观与抽象.
二.解导数问题基本思想策略
（1）若导函数的最高项系数为参数，需对最高项系数为正、负或零进行分类讨论；
（2）若需考虑判别式Δ，需对
（3）若导函数的几个零点大小不定时，需要结合定义域对零点的大小进行讨论；
三.基本方法：1.“将导数进行到底！”能看清一 个复杂问题的本质；2.用一点极限思想，会使研究函数 形态问题变得简单；3.画图，可看清讨论的分类标准.4.分离变量， 5.构造函数.6.整体代换. 7.正难则反
导函数的正负，注意到 ，故可考虑导函数的单调性。
分离变量 构造函数.
(1)如果一条直线与函数图像只有一个公共点，那么这条直线可以不是这个函数图像的切线.
(2)如果一条直线是这个函数图像的切线，那么这条直线与函数图像可以有多个公共点.
在某点处的导数是刻画函数的局部性质.
切线与函数图像的局部相切.
(3)函数在x0的局部图像未必位于在x0处切线的同侧.
(4)过函数图像上一点，有时可以做出多条切线.
(5) 利用导数未必求出经过函数图像外一点所有切线.
探究结果：(1)红色区域内的点和原点一条切线；(2)黑色边界线上的点（除原点外）两条切线；(3)黄色区域内的点三条切线.
二.求函数 单调区间
1.强化规范意识——少丢分的法宝！
2.分类讨论意识——多得分的法宝！
（1）若导函数的几个零点大小不定时，需要结合定义域对零点的大小进行讨论；
（2）若导函数的最高项系数为参数，需对最高项系数为正、负或零进行分类讨论；
（3）若需考虑判别式Δ，需对
零点定义：我们把使函数y＝ f(x) 的值为0的实数x，称为函数y＝f(x)的零点.
零点问题解题方法：1.直接解方程;2.零点存在性定理: 若函数y＝f(x)在区间[a，b]上的图象是一条不间断的曲线，且f(a)·f(b)<0，则函数y=f(x)在区间(a，b)上有零点.3.曲线公共点个数.
(1)（2013理9）函数f(x)=xcsx2在区间[0，4]上 的零点个数为（ ）． A．4 B．5 C．6 D．7
(2) （2014天津理4）函数f(x)=2x+x3–2在区间(0，1) 内的零点个数是（ ）． （A）0 　 （B）1　　（C）2　 （D）3
(3)函数 在区间 内的 零点个数是（ ）． （A）0 　 （B）1　　（C）2　 （D）3
由f(x)＝0得ax3－3x2＋1＝0，即ax3＝3x2－1，
由f(x)＝0得ax3－3x2＋1＝0，即ax3＝3x2－1，
五.恒成立问题、存在问题
双变量问题转化为单变量问题
解题策略：1.转化最值问题；2.构造新函数；3.分离变量.
1.转化为函数的最值问题；2.含零点式整体代入；3.利用基本函数图像；4.不等式的放缩.
1.转化为函数的最值问题
… … … 研究新函数
双变量转化为单变量问题