北师大版 (2019)选择性必修 第二册1.1 平均变化率综合训练题

【特供】1.1 平均变化率-2课时练习

一．填空题

1．

若函数，则f(x)在点(0，f(0))处切线的倾斜角为___________.

2．

已知一物体的运动方程是，则此物体在t=1和t=4时的瞬时速度分别为________.

3．

一物体的运动方程为s(t)＝7t2－13t＋8，则t0＝________时该物体的瞬时速度为1．

4．

曲线在x＝0处的切线方程是_________．

5．

已知曲线在处切线的斜率为1，则______．

6．

函数在处的切线方程为______.

7．

设抛物线：和：在它们的一个交点处的切线互相垂直，则过定点___________.

8．

已知函数在处的导数为11，则=___________.

9．

若f′(x0)＝2，则＝________．

10．

函数的图象在处的切线方程为___________.

11．

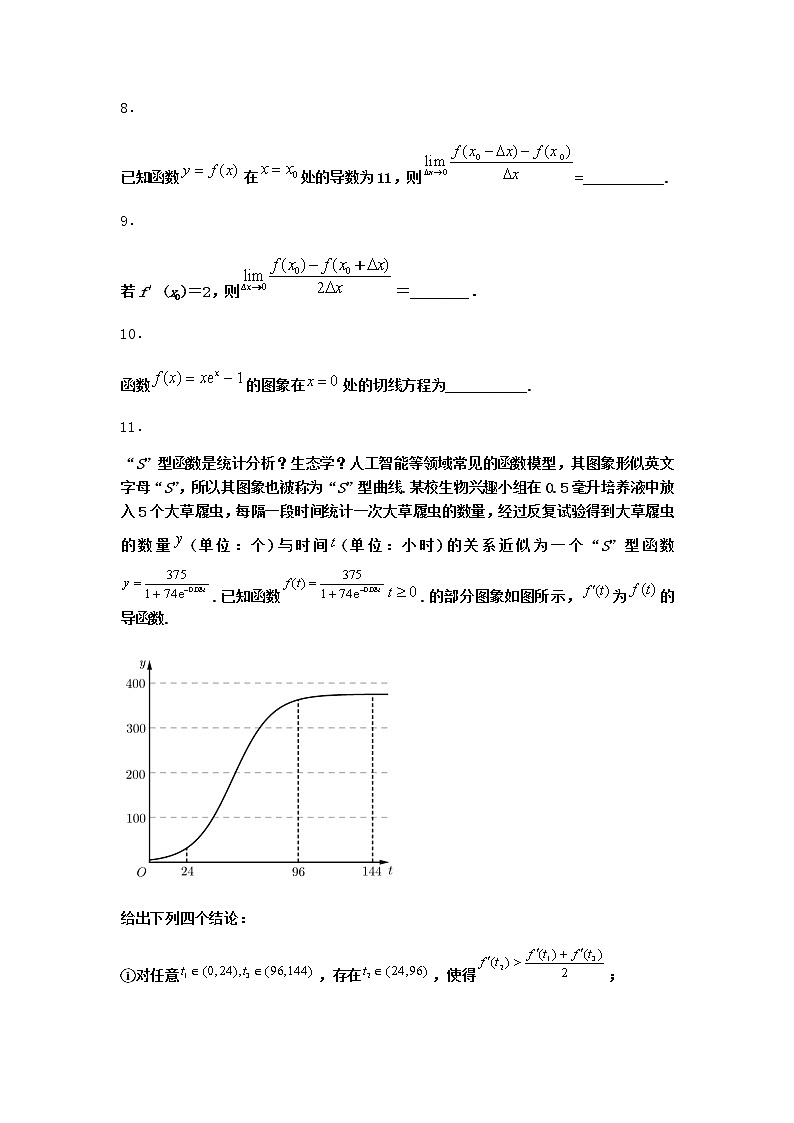
“S”型函数是统计分析？生态学？人工智能等领域常见的函数模型，其图象形似英文字母“S”，所以其图象也被称为“S”型曲线.某校生物兴趣小组在0.5毫升培养液中放入5个大草履虫，每隔一段时间统计一次大草履虫的数量，经过反复试验得到大草履虫的数量(单位：个)与时间(单位：小时)的关系近似为一个“S”型函数.已知函数.的部分图象如图所示，为的导函数.

给出下列四个结论：

①对任意，存在，使得；

②对任意，存在，使得；

③对任意，存在，使得；

④对任意，存在，使得.

其中所有正确结论的序号是___________.

12．

瑞士著名数学家欧拉在1765年证明了定理：三角形的外心．重心．垂心位于同一条直线上，这条直线被后人称为三角形的“欧拉线”.已知平面直角坐标系中为直角三角形，其直角顶点在轴上，点是斜边上一点，其“欧拉线”是正切曲线以点为切点的切线，则点的坐标为______.

13．

已知函数f(x)=xex﹣1，则曲线y=f(x)在x=1处的切线方程为___________.

14．

已知曲线在处切线的斜率为，则______．

15．

曲线在处的切线方程为______．

16．

已知函数有且只有一个零点，则______．

17．

曲线在点处的切线方程为___________.

18．

直线与曲线相切，也与曲线相切(其中e为自然对数的底数)，则___________.

参考答案与试题解析

1．【答案】

【解析】

解：由，得，

令 ，则，得

令，则，得

则f(x)在点(0，f(0))处切线的斜率为﹣1，

所以所求倾斜角为，

故答案为：.

2．【答案】6，6

【解析】

解：t=1时，

t=4时，

故答案为：6，6

3．【答案】1

【解析】

＝

＝(14t0－13＋7Δt)＝14t0－13＝1，得t0＝1．

故答案为：1

4．【答案】y＝﹣x+1

【解析】

的导数为，

可得曲线在x＝0处的切线的斜率为k＝﹣1，

又切点为（0，1），

所以切线的方程为y＝﹣x+1．

故答案为：y＝﹣x+1．

5．【答案】1

【解析】

函数的导数为，所以，

由条件曲线在处切线的斜率为1，

所以.

故答案为：1.

6．【答案】

【解析】

解：函数的导数为，

则函数在处的切线斜率为，

切点为，

则切线的方程为.

故答案为：.

7．【答案】

【解析】

解：，，

，，

设交点为，，

它们在一个交点处切线互相垂直，

，即，①

由交点分别代入二次函数式，整理得，

，即，②

由①②整理得，即，

所以，

令，可得，

则过定点，

故答案为：，

8．【答案】

【解析】

根据题意，由极限的性质可得＝，

又由函数f（x）在x＝x0处的导数为11，即＝11，故＝

故答案为：

9．【答案】－1

【解析】

.

故答案为：-1

10．【答案】

【解析】

函数的导数为，

所以在处的切线斜率为，切点为，

所以函数在处的切线方程为，

即.

故答案为：.

11．【答案】①②

【解析】

根据函数的图象可得导函数的图象（如图所示），

设导数在取最大值，结合的图象可知，

且当时，为增函数，在上为减函数，

对于①，任意，取，则有，故①成立.

对于②，设，由图象的性质可平移直线至处，

此时平移后的直线与图象相切，且，取，

故，故②正确.

对于③，取如图所示的，设，，过作横轴的平行线，

交的图象于，由函数的图象特征可得，

取，则，故③不成立.

对于④，取（为①中最大值点），

则过的切线“穿过”曲线，曲线上不存在与该切线平行的割线，

否则与导数存在唯一的最大值点矛盾，故④错误.

故答案为：①②.

12．【答案】

【解析】

因为是直角三角形，所以其垂心为直角顶点，其外心为斜边的中点，

故的“欧拉线”即为直线，

由题设知直线即为正切曲线以点为切点的切线，

又点在斜边上，故的外心即为点，

由

所以正切曲线在点处的切线的斜率为

故其“欧拉线”的方程为，

令，得，所以∴.

故答案为：

13．【答案】y=2x﹣1

【解析】

f′(x)=xex﹣1+ex﹣1

f′（1）=2，f（1）=1，

故切线方程是：y﹣1=2(x﹣1)，

即y=2x﹣1；

故答案为：y=2x﹣1.

14．【答案】

【解析】

对函数求导得，

由已知条件可得，解得.

故答案为：.

15．【答案】

【解析】

因为，

所以，

所以，

所以曲线在处的切线方程为，

即，

故答案为：

16．【答案】

【解析】

令，，

有且只有一个零点，

与有一个交点，即两曲线在交点处有公切线，设切点为，

，，

，即 ，代入到中，即 ，

化简得：，

即，

，.

故答案为：

17．【答案】

【解析】

解：，则，则切线方程为，

故答案为：.

18．【答案】e

【解析】

由题设知：，则；，则.

∴要使与．都相切，若切点分别为，则有，

∴，则，

∴.

故答案为：.