



初中数学青岛版九年级下册5.1函数与它的表示法课文ppt课件
展开1.认识分段函数.2.会根据简单分段函数的表达式或图象求函数值.
为了鼓励节约用电,某市按以下标准对居民用户收取电费:当一户居民月用电量不超过200 kW·h时,按0.5元/kW·h收费.当一户居民月用电量超过200 kW·h时,超过部分按0.7元/kW·h收费.(1)设用电量为x kW·h,电费为y元,你能按上述标准写出一户居民的每月应缴电费y(元)与x(kW·h)之间的函数表达式吗?(2)你能用描点法画出这个函数的图象吗?与同学交流.
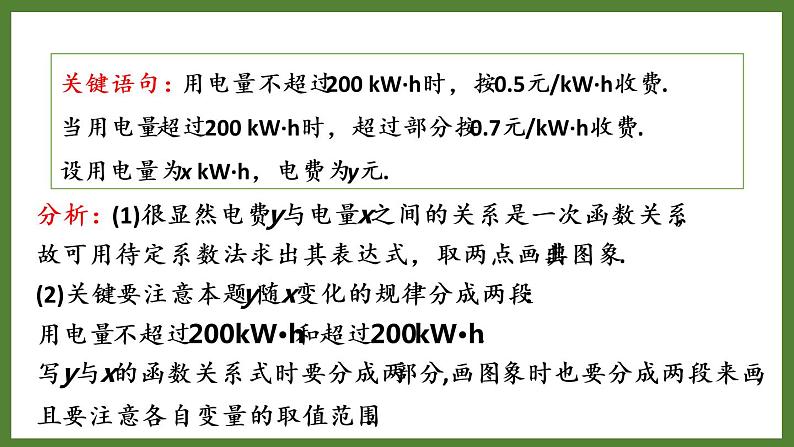
分析:(1)很显然电费y与电量x之间的关系是一次函数关系,故可用待定系数法求出其表达式,取两点画出其图象.(2)关键要注意本题y随x变化的规律分成两段:用电量不超过200kW·h和超过200kW·h.写y与x的函数关系式时要分成两部分,画图象时也要分成两段来画,且要注意各自变量的取值范围.
关键语句:用电量不超过200 kW·h时,按0.5元/kW·h收费. 当用电量超过200 kW·h时,超过部分按0.7元/kW·h收费.设用电量为x kW·h,电费为y元.
解:(1)当 0≤ x ≤ 200 时, y = 0.5x;
当 x > 200 时,
y =0.5× 200 + 0.7×(x – 200) = 0.7x - 40 .
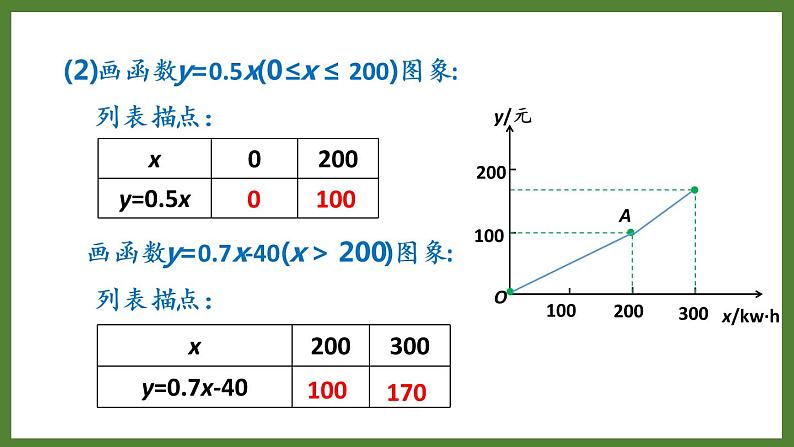
(2)画函数y=0.5x(0≤x ≤ 200)图象:
画函数y=0.7x-40(x > 200)图象:
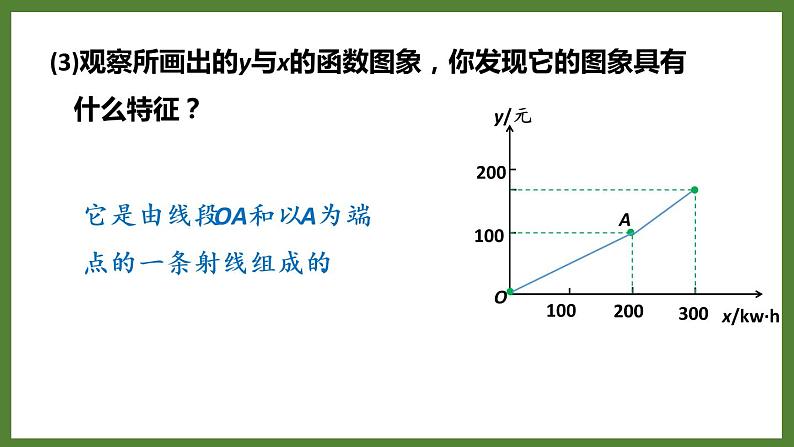
(3)观察所画出的y与x的函数图象,你发现它的图象具有 什么特征?
它是由线段OA和以A为端点的一条射线组成的.
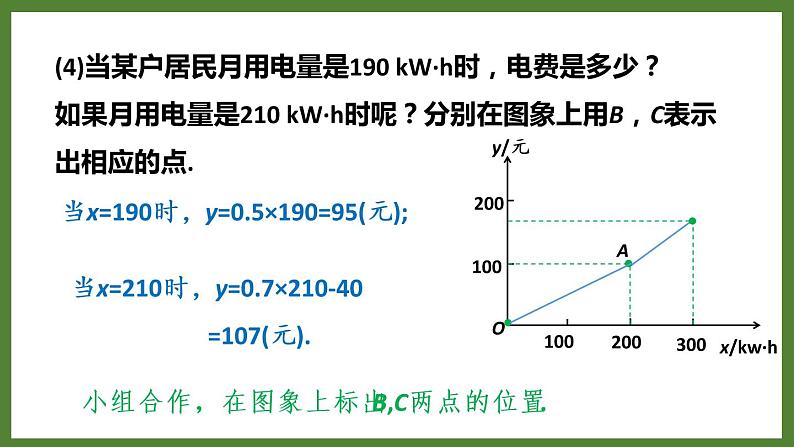
(4)当某户居民月用电量是190 kW·h时,电费是多少?如果月用电量是210 kW·h时呢?分别在图象上用B,C表示出相应的点.
当x=190时,y=0.5×190=95(元);
当x=210时,y=0.7×210-40 =107(元).
小组合作,在图象上标出B,C两点的位置.
(5)图中点A是图象中线段OA的一个端点,又是射线AC的端点,因此,它是图象上的一个分段点. 你发现分段点与图象上其他点的区别是什么?
随着自变量的增加,当图象上的点经过分段点时,函数的对应关系发生了变化:分段点左边函数关系满足 y = 0.5x,右边满足 y = 0.7x - 40.
如果函数关系是分段给出的,这样的函数叫做分段函数.
分段函数反映在函数表达式方面,每一段都有函数表达式,前后两段函数表达式不同.反映在函数图象上,图象有分段点,分段点前后图象不是同一发展趋势,有的分段点既是上一段函数图象的“终点”,也是下一段函数图象的“起点”.
某校住校生放学后到学校锅炉房水箱打水,每人接水2 L. 开始时水箱中有水96 L,两个龙头同时放水,经过2 min后,水箱内的余水量为80 L. 此时其中一个龙头因故障而关闭. 如果前后两人接水间隔时间忽略不计,且不发生泼洒,水箱内的余水量y(L)与放水时间x(min)的函数图象如图所示. 已知放水4 min时,水箱中的余水量为72 L.
(1)写出水箱的余水量y与放水时间x之间的函数表达式;
解:(1)根据题意及图象,可知,y与x之间的函数是分段函数.其中线段AB表示两个水龙头同时放水时y与x的对应关系.
同样地将(2,80),(4,72)代入y=k2x+b2,可以求出当只有一个水龙头放水时,y与x之间函数的表达式为y=-4x+88.令y=0,得x=22(min).所以当只有一个水龙头放水时,函数表达式是y=-4x+88,2<x≤22.
(2)前15位同学接水共用了多少时间?
(2)前15位同学共接水2×15=30(L),当第15位同学接完水时水箱余量为96-30=66<80.由图可以看出,此时只有一个水龙头放水.将y=66代入y=-4x+88,得66=-4x+88,解得x=5.5(min).所以,前15位同学接水共用时间5.5min.
天泉村服装厂今年前5个月中生产服装的总件数S(件)与时间t(月)的函数关系如图所示.在下面的四个说法中,你能判断哪个是正确的吗?
(A)1月至3月每月生产总件数逐月增加, 4,5两月每月生产总件数逐月减少(B)1月至3月每月生产总件数逐月增加,4,5两月停止生产(C)1月至3月每月生产总件数逐月增加,4,5两月每月生产总件数与3月持平(D)1月至3月每月生产总件数不变,4,5两月停止生产
解:S代表前5个月生产服装的总件数,而不是当月的件数,所以1月至3月每月生产的总件数相等,4,5两月总件数维持3月末时的总件数,所以4,5两月停止生产.所以说法D正确.
某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后:(1)服药后____时,血液中含药量最高,达到每毫升_______毫克.(2)服药5时,血液中含药量为每毫升____毫克.(3)当x≤2时,y与x之间的函数关系式是________.
某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后:(4)当x≥2时,y与x之间的函数关系式是_________.(5)如果每毫升血液中含药量3毫克或3毫克以上时,治疗疾病最有效,那么这个有效时间是___ 小时.
初中数学青岛版九年级下册5.1函数与它的表示法教课内容课件ppt: 这是一份初中数学青岛版九年级下册5.1函数与它的表示法教课内容课件ppt,共16页。PPT课件主要包含了学习目标,合作探究,≤t≤21,唯一确定,≤x≤40,≤t≤10,是任意实数,是x≥0,任意实数,不为零等内容,欢迎下载使用。
初中数学青岛版九年级下册5.1函数与它的表示法教学演示ppt课件: 这是一份初中数学青岛版九年级下册5.1函数与它的表示法教学演示ppt课件,共19页。PPT课件主要包含了学习目标,复习导入,观察与思考,2解析法,是函数关系,≤x≤40,归纳与总结,达标练习,2t10分钟,s=2t等内容,欢迎下载使用。
青岛版九年级下册5.3二次函数示范课ppt课件: 这是一份青岛版九年级下册5.3二次函数示范课ppt课件,共16页。PPT课件主要包含了学习目标,复习回顾,yax2+c,yax–h2,yax2,比较与探究,解1列表,2描点,3画图,开口向上等内容,欢迎下载使用。













