河北省承德市平泉市回民中学2022-2023学年九年级上学期期末考试数学试题(含答案)

河北省承德市平泉市回民中学2022-2023学年九年级上学期期末考试数学试题

学校:___________姓名：___________班级：___________考号：___________

一、单选题

1．一元二次方程的二次项系数、一次项系数、常数项分别是（    ）

A．1、2、 B．1、2、4 C．1、、4 D．1、、

2．已知二次函数的解析式为，则图象的顶点坐标是（    ）

A． B． C． D．

3．关于x的方程x2＋4kx＋2k2＝4的一个解是﹣2，则k值为（    ）

A．2或4 B．0或4 C．﹣2或0 D．﹣2或2

4．2022北京冬奥会吉祥物“冰墩墩”以熊猫为原型进行设计创作，如图，旋转吉祥物“冰墩墩”可以得到的图形是（    ）

A． B． C． D．

5．用反证法证明命题“在直角三角形中，必有一个锐角不小于45°”时，首先应假设这个直角三角形中（  ）

A．两个锐角都大于45°       B．两个锐角都小于45°

C．两个锐角都不大于45°    D．两个锐角都等于45°

6．若两个图形成中心对称，则下列说法：

①对应点的连线必经过对称中心；②这两个图形的形状和大小完全相同；

③这两个图形的对应线段一定相等；④将一个图形绕对称中心旋转某个角度后必与另一个图形重合．

其中正确的有（   )

A．1个 B．2个 C．3个 D．4个

7．如图，正六边形内接于．连接．则的度数是（    ）

A．  B． C． D．

8．把一副普通扑克牌中的5张洗匀后，正面向下放在桌子上，其中有1张“黑桃”，2张“梅花”和2张“红桃”，从中随机抽取一张，恰好是“梅花”的概率是（    ）

A． B． C． D．

9．下列关于二次函数有如下说法：①图象的开口向上；②图象最低点到轴的距离为；③图象的对称轴为直线；④当时，随的增大而增大．其中所有正确结论的序号是（    ）

A．①② B．①③ C．②④ D．③④

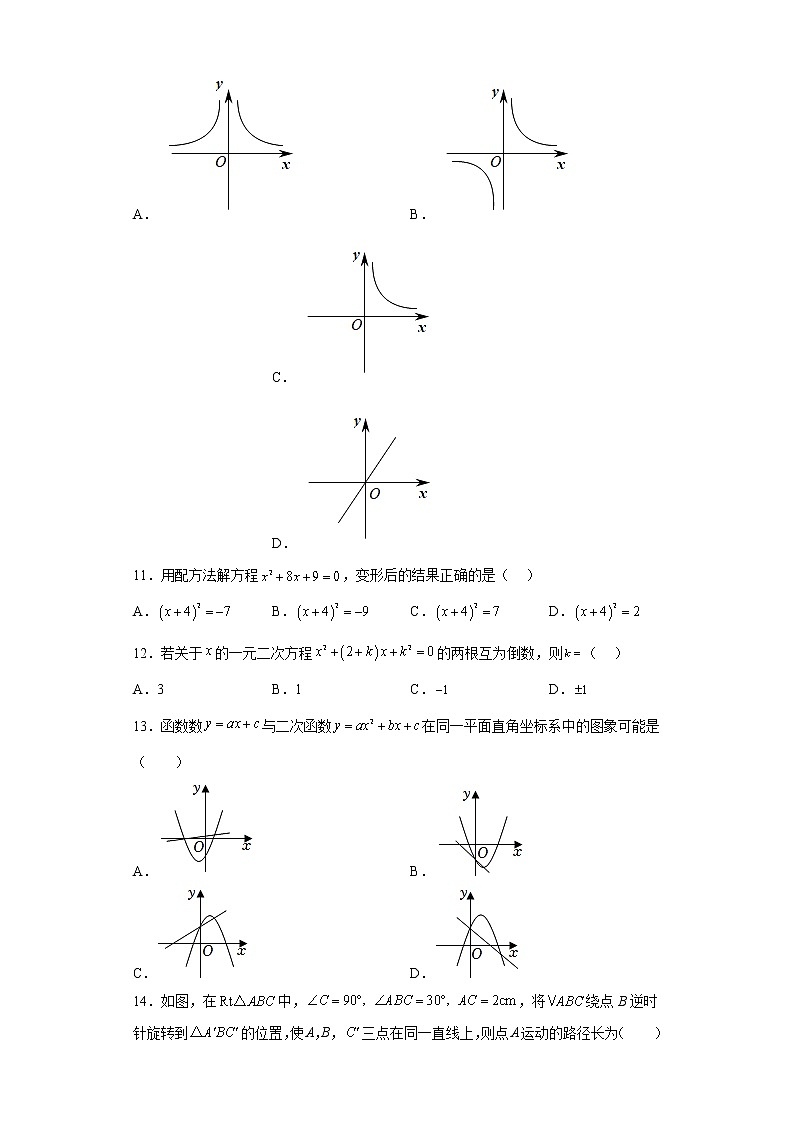
10．如果三角形的面积为，那么它的底边与高之间的函数关系用下列图象表示大致是（　　）

A． B． C． D．

11．用配方法解方程，变形后的结果正确的是（    ）

A． B． C． D．

12．若关于的一元二次方程的两根互为倒数，则（    ）

A．3 B．1 C． D．

13．函数数与二次函数在同一平面直角坐标系中的图象可能是（　　）

A． B．

C． D．

14．如图，在中，，将绕点B逆时针旋转到的位置，使A，B，三点在同一直线上，则点A运动的路径长为（　　）

A． B． C． D．

15．如图，在平面直角坐标系中，点A是反比例函数的图像上的一点，过点A作轴于点B，C在y轴的负半轴上，连接．若的面积为8，则m的值为（　　）

A． B．16 C． D．8

16．已知，在中，，求作的外心O，以下是甲、乙两同学的作法：

对于两人的作法，正确的是（    ）

A．两人都对 B．两人都不对

C．甲对，乙不对 D．甲不对，乙对

17．如图，已知二次函数的图象与轴有两个交点的横坐标分别为和4，则当时，的取值范围是（    ）

A． B． C． D．或

18．如图，在Rt△ABC中，∠C＝90°，AC＝3，BC＝4，以点A为圆心作圆，如果圆A与线段BC没有公共点，那么圆A的半径r的取值范围是(　　)

A．5≥r≥3 B．3＜r＜5 C．r＝3或r＝5 D．0＜r＜3或r＞5

19．如图，将抛物线图象中轴上方的部分沿轴翻折到轴下方，图象的其余部分不变，得到一个新图象（实线部分），则新图象与直线的交点个数有（）

A．4个 B．3个 C．2个 D．1个

20．已知二次函数的部分函数图象如图所示，则一次函数与反比例函数在同一平面直角坐标系中的图象大致是（　　）

A． B． C． D．

二、填空题

21．某园艺公司准备围建一个矩形花圃，其中一边靠墙（墙长20米），另外三边用篱笆围成如图所示，所用的篱笆长为32米．请问当垂直于墙的一边的长为____米时，花圃的面积有最大值，最大值是____．

22．如图，点A坐标为，点B坐标为，C为上一个动点，分别以、为斜边在的同侧作两个等腰直角三角形和，连结．

（1）线段的长为_______．

（2）则长的最小值是_______．

23．如图所示，P是外一点，，分别和切于A，B两点，C是上任意一点，过C作的切线分别交，于D，E．

（1）若的周长为10，则的长为________；

（2）连接、，若，则的度数为________度．

24．如图，平面直角坐标系中，△OA1B1是边长为2的等边三角形，作△B2A2B1与△OA1B1关于点B1成中心对称，再作△B2A3B3与△B2A2B1于点B2成中心对称，如此作下去，则△B2020A2021B2021的顶点A2021的坐标是___

三、解答题

25．某校为落实“双减”工作，增强课后服务的吸引力，充分用好课后服务时间，为学有余力的学生拓展学习空间，成立了5个活动小组（每位学生只能参加一个活动小组）：A．音乐；B．体育；C．美术；D．阅读；E．人工智能．为了解学生对以上活动的参与情况，随机抽取部分学生进行了调查统计，并根据统计结果，绘制了如图所示的两幅不完整的统计图．

根据图中信息，解答下列问题：

(1)①此次调查一共随机抽取了________名学生；

②补全条形统计图（要求在条形图上方注明人数）；

③扇形统计图中圆心角________度；

(2)若该校有3200名学生，估计该校参加D组（阅读）的学生人数；

(3)刘老师计划从E组（人工智能）的甲、乙、丙、丁四位学生中随机抽取两人参加市青少年机器人竞赛，请用树状图法或列表法求出恰好抽中甲、乙两人的概率．

26．在中，，直线经过点C，且于D，于E．

(1)当直线绕点C旋转到图1的位置时，求证：

①；

②．

(2)当直线绕点C旋转到图2的位置时，求证：；

(3)当直线绕点C旋转到图3的位置时，试问具有怎样的等量关系？请写出这个等量关系，并加以证明．

27．如图，一次函数与反比例函数的图象交于，两点．

(1)求一次函数的解析式；

(2)根据图象直接写出的的取值范围；

(3)求的面积．

28．某校为配合疫情防控需要，每星期组织学生进行核酸抽样检测；防疫部门为了解学生错峰进入操场进行核酸检测情况，调查了某天上午学生进入操场的累计人数y（单位：人）与时间x（单位：分钟）的变化情况，发现其变化规律符合函数关系式：数据如下表．

(1)求a，b，c的值；

(2)如果学生一进入操场就开始排队进行核酸检测，检测点有4个，每个检测点每分钟检测5人，求排队人数的最大值（排队人数-累计人数-已检测人数）；

(3)在（2）的条件下，全部学生都完成核酸检测需要多少时间？如果要在不超过20分钟让全部学生完成核酸检测，从一开始就应该至少增加几个检测点？

参考答案：

1．D

2．C

3．B

4．A

5．B

6．C

7．D

8．C

9．B

10．C

11．C

12．B

13．D

14．A

15．A

16．C

17．D

18．D

19．B

20．B

21．     8     128平方米##128m2

22．     7    

23．     5     115

24．

25．(1)①200；②见解析；③54

(2)1120

(3)

26．(1)①见解析；②见解析

(2)见解析

(3)，证明见解析

27．(1)

(2)或

(3)8

28．(1)，，

(2)490人

(3)从一开始应该至少增加3个检测点