高中数学人教A版 (2019)必修 第二册6.3 平面向量基本定理及坐标表示课文内容课件ppt

这是一份高中数学人教A版 (2019)必修 第二册6.3 平面向量基本定理及坐标表示课文内容课件ppt，共44页。PPT课件主要包含了内容索引，课前篇自主预习，课堂篇探究学习，激趣诱思，知识点拨，答案A，答案C，答案75，答案4等内容，欢迎下载使用。

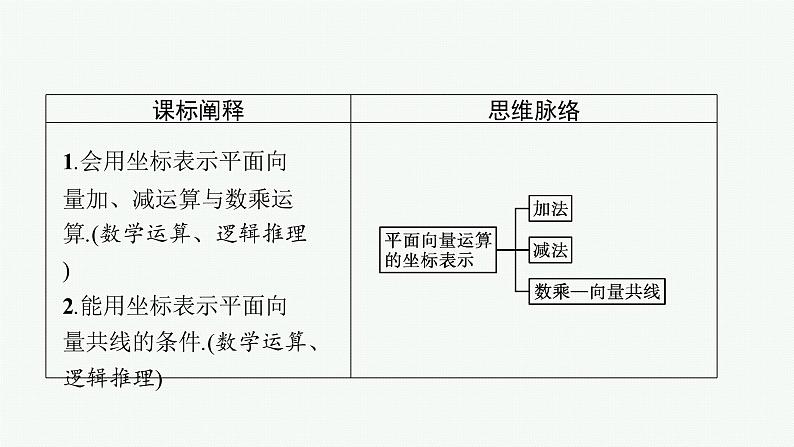
1.会用坐标表示平面向量加、减运算与数乘运算.(数学运算、逻辑推理)2.能用坐标表示平面向量共线的条件.(数学运算、逻辑推理)
我们已经学习了向量的坐标表示,那向量的线性运算能用坐标表示吗?同学,你能自行推导吗?
知识点一、平面向量运算的坐标表示平面向量的坐标运算法则:若向量a=(x1,y1),b=(x2,y2),λ∈R,则
微练习(1)若a=(3,-2),b=(-1,4),则2a+3b=　　　　　. 
答案 (1)(3,8)　(2)(2,10)　(-2,-10)
知识点二、平面向量共线的坐标表示
若再转化为更一般的情况,可得:a1b2-a2b1=0.这是两向量共线坐标条件的一般化表示,适用于任意两向量共线.
微思考向量共线定理的内容是什么?提示向量a(a≠0)与b共线的充要条件是:存在唯一一个实数λ,使b=λa.
微练习(1)下列各组向量共线的是(　　)A.a=(1,2),b=(4,2)B.a=(1,0),b=(0,2)C.a=(0,-2),b=(0,2)D.a=(-3,2),b=(-6,-4)(2)若向量m=(3,-2)与n=(x,4)共线,则实数x=　　　　　. 答案 (1)C　(2)-6解析(1)C选项中,b=-a,所以a与b共线,其余各组向量均不共线.(2)因为两个向量共线,所以3×4=(-2)×x,解得x=-6.
分析(1)可直接运用坐标运算法则进行计算.(2)应先求出相关向量的坐标,再运用法则计算.
解 (1)因为a=(1,2),b=(3,-4),c=(-2,6),所以a+3b=(1,2)+3(3,-4)=(1,2)+(9,-12)=(10,-10),
反思感悟 向量坐标运算要注意的问题(1)向量的坐标运算主要是利用加法、减法、数乘运算法则进行,若已知有向线段两端点的坐标,则应先求出向量的坐标,要注意三角形法则及平行四边形法则的应用.(2)若是给出向量的坐标,解题过程中要注意方程思想的运用及正确使用运算法则.(3)向量线性运算的坐标表示可完全类比数的运算进行.
A.(4,6) B.(-4,-6)C.(-2,-2)D.(2,2)
求解;也可将题中所给向量式中向量的起点全都转化为以原点O为起点,再利用其终点坐标就是向量坐标这一性质求解.(2)可利用平面向量基本定理建立等量关系,代入坐标利用向量相等得到参数的值.
反思感悟 平面向量坐标运算应用技巧(1)坐标形式下向量相等的条件:相等向量的对应坐标相等;对应坐标相等的向量是相等向量.由此可建立相等关系求某些参数的值.(2)利用坐标运算求向量的基底表示,一般先求基底向量和被表示向量的坐标,再利用待定系数法.设c=xa+yb,在求解时要运用相等向量坐标相同的关系列方程(组)求出x,y的值.
分析首先根据点的坐标求出向量 的坐标,然后利用向量共线的条件判断证明.
变式训练2判断下列向量a与b是否平行:
例4已知向量a=(-1,x),b=(x-2,-3),若向量2a+b与向量3a-2b共线,求实数x的值.分析首先求出向量2a+b与向量3a-2b的坐标,然后根据向量共线的坐标表示建立方程求解.
解 因为a=(-1,x),b=(x-2,-3),所以2a+b=(x-4,2x-3),3a-2b=(-2x+1,3x+6).因为向量2a+b与向量3a-2b共线,所以(x-4)(3x+6)=(2x-3)(-2x+1),整理得x2-2x-3=0,解得x=3或x=-1.故实数x的值是3或-1.
要点笔记根据向量共线求参数值的方法根据向量共线的条件求参数值的问题,一般有两种处理思路,一是利用向量共线定理a=λb(b≠0)列方程组求解,二是利用向量共线的坐标表达式x1y2-x2y1=0或
延伸探究本例中,若已知“向量a=(-1,x),b=(x-2,-3)反向”,如何求实数x的值?
解 (方法一)由题意可知向量a=(-1,x),b=(x-2,-3)共线,则有(-1)×(-3)=x(x-2),即x2-2x-3=0,解得x=3或x=-1.当x=3时,a=(-1,3),b=(1,-3),这时a=-b,a与b反向;当x=-1时,a=(-1,-1),b=(-3,-3),这时3a=b,a与b同向,故实数x的值为3.(方法二)因为向量a=(-1,x),b=(x-2,-3)反向,所以设a=λb(λ<0),即(-1,x)=λ(x-2,-3),
因为λ<0,所以取x=3,故实数x的值为3.
反思感悟 三点共线的实质与证明步骤(1)实质:三点共线问题的实质是向量共线问题.两个向量共线只需满足方向相同或相反.(2)证明步骤:①证明向量平行;②证明两个向量有公共点.
于是1×(m+1)-m×2=0,解得m=1.若点A,B,C能构成三角形,则点A,B,C不共线,故m≠1.
线段定比分点的坐标公式及应用1.线段定比分点的定义
2.定比分点的坐标表示
典例线段M1M2的端点M1,M2的坐标分别为(1,5),(2,3),且 ,则点M的坐标为(　　)A.(3,8)B.(1,3)C.(3,1)D.(-3,-1)
1.已知a=(-3,2),b=(2,3),则2a-3b等于(　　)A.(-12,5)B.(12,5)C.(-12,-5)D.(12,-5)答案 C解析 2a-3b=2(-3,2)-3(2,3)=(-6,4)-(6,9)=(-12,-5).
2.(多选题)下列各组向量中,不能组成基底的是(　　)A.e1=(0,0),e2=(1,1)B.e1=(1,2),e2=(-2,1)
D.e1=(2,6),e2=(-1,-3)答案 ACD解析 A,C,D中向量e1与e2共线,不能组成基底;B中e1,e2不共线,所以可组成一个基底.
3.(2021黑龙江香坊校级三模)已知向量a=(1,2),b=(m,m+3),若a∥b,则m=(　　)A.-7B.-3C.3D.7答案 C解析 ∵a∥b,∴m+3-2m=0,解得m=3.故选C.
4.已知a=(3,4),点A(1,-3),若 =2a,则点B的坐标为　　　　　　　　. 
(1)点P在第一、第三象限角平分线上;(2)点P在第三象限内.