

初中数学中考复习 专题10 二次函数【考点精讲】(解析版)
展开专题10 二次函数
知识导航
知识精讲
考点1:二次函数的图象和性质
1.二次函数的一般形式:y=ax2+bx+c (a,b,c是常数,a≠0)
注:未知数的最高次数是2,a≠0,b,c是任意实数。
2.函数图象和性质
函数
二次函数y=ax2+bx+c(a,b,c为常数,a≠0)
图象
a>0
a<0
性质
①当a>0时,抛物线开口向上,并向上无限延伸.
②对称轴是,顶点坐标是.
③在对称轴的左侧,即当x<时,y随x的增大而减小;在对称轴的右侧,即当x>时,y随x的增大而增大,简记为左减右增.
④抛物线有最低点,当x=时,y有最小值,y最小值=.
①当a<0时,抛物线开口向下,并向下无限延伸.
②对称轴是,顶点坐标是.
③在对称轴的左侧,即当x<时,y随x的增大而增大;在对称轴的右侧,即当x>时,y随x的增大而减小,简记为左增右减.
④抛物线有最高点,当x=时,y有最大值,y最大值=.
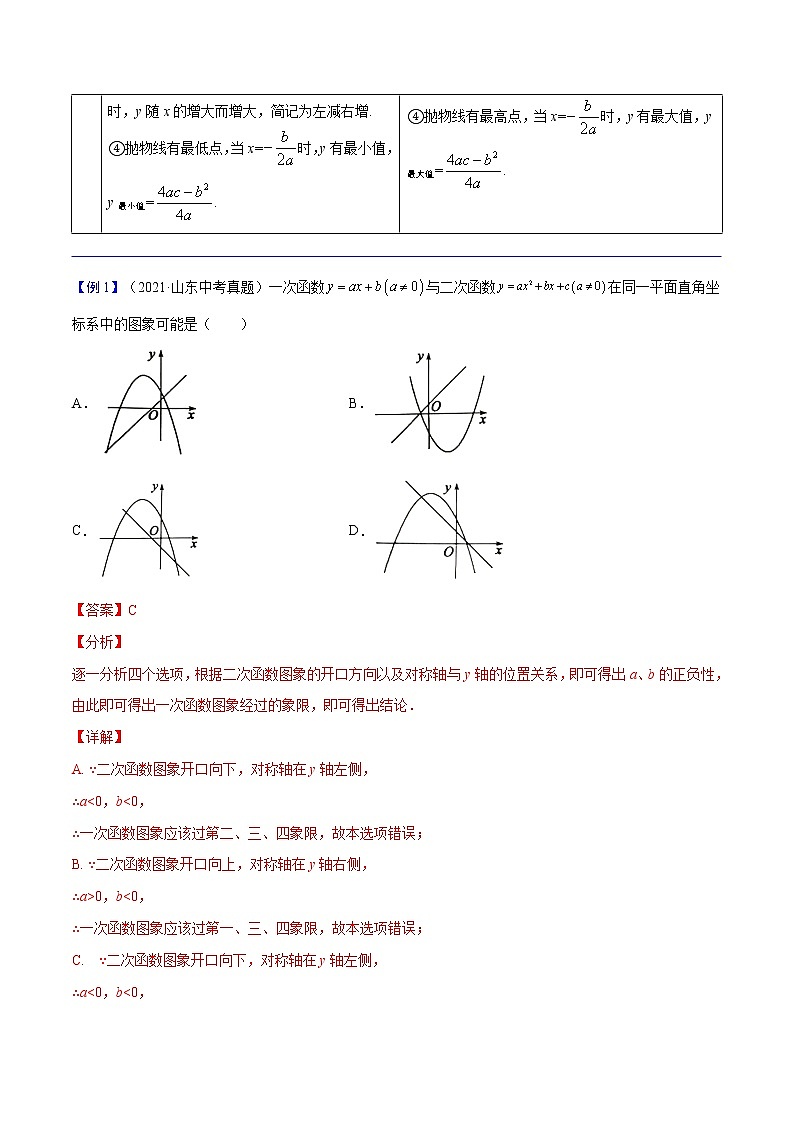
【例1】(2021·山东中考真题)一次函数与二次函数在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
【答案】C
【分析】
逐一分析四个选项,根据二次函数图象的开口方向以及对称轴与y轴的位置关系,即可得出a、b的正负性,由此即可得出一次函数图象经过的象限,即可得出结论.
【详解】
A. ∵二次函数图象开口向下,对称轴在y轴左侧,
∴a<0,b<0,
∴一次函数图象应该过第二、三、四象限,故本选项错误;
B. ∵二次函数图象开口向上,对称轴在y轴右侧,
∴a>0,b<0,
∴一次函数图象应该过第一、三、四象限,故本选项错误;
C. ∵二次函数图象开口向下,对称轴在y轴左侧,
∴a<0,b<0,
∴一次函数图象应该过第二、三、四象限,故本选项正确;
D. ∵二次函数图象开口向下,对称轴在y轴左侧,
∴a<0,b<0,
∴一次函数图象应该过第二、三、四象限,故本选项错误.
故选C.
【例2】(2021·四川中考真题)如图,已知抛物线(,,为常数,)经过点,且对称轴为直线,有下列结论:①;②;③;④无论,,取何值,抛物线一定经过;⑤.其中正确结论有( )
A.1个 B.2个 C.3个 D.4个
【答案】D
【分析】
①根据图像开口向上,对称轴位置,与y轴交点分别判断出a,b,c的正负
②根据对称轴公式,判断的大小关系
③根据时,,比较与0的大小;
④根据抛物线的对称性,得到与时的函数值相等结合②的结论判断即可
⑤根据抛物线对称轴找到顶点坐标的纵坐标,比较任意一点与顶点的纵坐标值,即比较函数值的大小即可判断结论.
【详解】
①图像开口朝上,故 ,根据对称轴“左同右异”可知,
图像与y轴交点位于x轴下方,可知c<0
故①正确;
②得
故②错误;
③经过
又由①得c<0
故③正确;
④根据抛物线的对称性,得到与时的函数值相等
当时,即
即
经过,即经过
故④正确;
⑤当时,, 当时,
函数有最小值
化简得,
故⑤正确.
综上所述:①③④⑤正确.
故选D.
方法技巧
抛物线y=ax2+bx+c中a,b,c的作用
(1)a决定开口方向及开口大小,这与y=ax2中的a完全一样.
a>0时,抛物线开口向上;a<0时,抛物线开口向下;a的绝对值越大,开口越小.
(2)b和a共同决定抛物线对称轴的位置.由于抛物线y=ax2+bx+c的对称轴是直线,故:①b=0时,对称轴为y轴;②>0(即a,b同号)
时,对称轴在y轴左侧;③<0(即a,b异号)时,对称轴在y轴右侧.(口诀:“左同右异”)
【注意问题】
(1)二次函数的图象与系数的关系;
(2)会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换.
针对训练
1.(2021·湖南中考真题)若二次函数的图象如图所示,则一次函数与反比例函数在同一个坐标系内的大致图象为( )
A. B. C. D.
【答案】D
【分析】
先根据抛物线的开口方向确定a<0,对称轴可确定b的正负,与y轴的交点可知c>0,然后逐项排查即可.
【详解】
解:∵抛物线开口方向向下
∴a<0,
∵抛物线对称轴
∴b>0
∵抛物线与y轴的交点在y轴的正半轴
∴c>0
∴的图像过二、一、四象限,的图象在二、四象限
∴D选项满足题意.
故选D.
2.(2021·福建中考真题)二次函数的图象过四个点,下列说法一定正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
【答案】C
【分析】
求出抛物线的对称轴,根据抛物线的开口方向和增减性,根据横坐标的值,可判断出各点纵坐标值的大小关系,从而可以求解.
【详解】
解:二次函数的对称轴为:
,且开口向上,
距离对称轴越近,函数值越小,
,
A,若,则不一定成立,故选项错误,不符合题意;
B,若,则不一定成立,故选项错误,不符合题意;
C,若,所以,则一定成立,故选项正确,符合题意;
D,若,则不一定成立,故选项错误,不符合题意;
故选:C.
3.(2021·湖北中考真题)二次函数的图象的一部分如图所示.已知图象经过点,其对称轴为直线.下列结论:①;②;③;④若抛物线经过点,则关于的一元二次方程的两根分别为,5,上述结论中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
【答案】C
【分析】
根据二次函数的图象与性质进行逐项判断即可求解.
【详解】
解:①由图象可知,a<0,b>0,c>0,
∴abc<0,故①正确;
②∵对称轴为直线x= =1,且图象与x轴交于点(﹣1,0),
∴图象与x轴的另一个交点坐标为(3,0),b=﹣2a,
∴根据图象,当x=2时,y=4a+2b+c>0,故②错误;
③根据图象,当x=﹣2时,y=4a﹣2b+c=4a+4a+c=8a+c<0,故③正确;
④∵抛物线经过点,
∴根据抛物线的对称性,抛物线也经过点,
∴抛物线与直线y=n的交点坐标为(﹣3,n)和(5,n),
∴一元二次方程的两根分别为,5,
故④正确,
综上,上述结论中正确结论有①③④,
故选:C.
考点2:二次函数的平移
1.抛物线y=a(x-h)2+k与y=ax2的关系
(1)二者的形状相同,位置不同,y=a(x-h)2+k是由y=ax2通过平移得来的,平移后的顶点坐标为(h,k).
(2)y=ax2的图象
右左
上下
y=a(x-h)2的图象
y=a(x-h)2+k的图象.
口诀:上加下减,左加右减
【例3】(2020•广东)把函数y=(x﹣1)2+2图象向右平移1个单位长度,平移后图象的的数解析式( )
A.y=x2+2 B.y=(x﹣1)2+1 C.y=(x﹣2)2+2 D.y=(x﹣1)2﹣3
【分析】先求出y=(x﹣1)2+2的顶点坐标,再根据向右平移横坐标加,求出平移后的二次函数图象顶点坐标,然后利用顶点式解析式写出即可.
【解析】二次函数y=(x﹣1)2+2的图象的顶点坐标为(1,2),
∴向右平移1个单位长度后的函数图象的顶点坐标为(2,2),
∴所得的图象解析式为y=(x﹣2)2+2.
故选:C.
方法技巧
图像平移规律:由函数y=ax2平移得到y=a(x-h)2+k满足“h值正右移,负左移;k值正上移,负下移”,概括成八个字,即:“左加右减,上加下减”.
针对训练
1.(2021·上海中考真题)将抛物线向下平移两个单位,以下说法错误的是( )
A.开口方向不变 B.对称轴不变 C.y随x的变化情况不变 D.与y轴的交点不变
【分析】根据二次函数的平移特点即可求解.
【详解】
将抛物线向下平移两个单位,开口方向不变、对称轴不变、故y随x的变化情况不变;与y轴的交点改变
故选D.
2.(2020•绥化)将抛物线y=2(x﹣3)2+2向左平移3个单位长度,再向下平移2个单位长度,得到抛物
线的解析式是( )
A.y=2(x﹣6)2 B.y=2(x﹣6)2+4
C.y=2x2 D.y=2x2+4
【分析】根据“左加右减、上加下减”的原则进行解答即可.
【详解】将将抛物线y=2(x﹣3)2+2向左平移3个单位长度所得抛物线解析式为:y=2(x﹣3+3)2+2,即y=2x2+2;
再向下平移2个单位为:y=2x2+2﹣2,即y=2x2.
故选:C.
3.(2020•哈尔滨)将抛物线y=x2向上平移3个单位长度,再向右平移5个单位长度,所得到的拋物线
为( )
A.y=(x+3)2+5 B.y=(x﹣3)2+5 C.y=(x+5)2+3 D.y=(x﹣5)2+3
【分析】根据“上加下减,左加右减”的原则进行解答即可.
【详解】由“上加下减”的原则可知,将抛物线y=x2向上平移3个单位所得抛物线的解析式为:y=x2+3;
由“左加右减”的原则可知,将抛物线y=x2+3向右平移5个单位所得抛物线的解析式为:y=(x﹣5)2+3;
故选:D.
考点3:二次函数与方程、不等式的关系
1.二次函数与一元二次方程的关系
二次函数图象与x轴的交点有三种情况:有两个交点、有一个交点、没有交点。当图象与x轴有交点时,令y=0,解方程ax2+bx+c=0就可求出与x轴交点的横坐标。
Δ=b2-4ac
ax2+bx+c=0的根
抛物线y=ax2+bx+c与x轴的交点
Δ>0
两个不相等的实数根
两个交点
Δ=0
两个相等的实数根
一个交点
Δ<0
无实数根
无交点
2.二次函数与不等式的关系
设抛物线y=ax2+bx+c(a>0)与x轴交于(x1,0),(x2,0)两点,其中x1
【例4】(2021·浙江中考真题)已知和均是以为自变量的函数,当时,函数值分别为和,若存在实数,使得,则称函数和具有性质.以下函数和具有性质的是( )
A.和 B.和
C.和 D.和
【答案】A
【分析】
根据题中所给定义及一元二次方程根的判别式可直接进行排除选项.
【详解】
解:当时,函数值分别为和,若存在实数,使得,
对于A选项则有,由一元二次方程根的判别式可得:,所以存在实数m,故符合题意;
对于B选项则有,由一元二次方程根的判别式可得:,所以不存在实数m,故不符合题意;
对于C选项则有,化简得:,由一元二次方程根的判别式可得:,所以不存在实数m,故不符合题意;
对于D选项则有,化简得:,由一元二次方程根的判别式可得:,所以不存在实数m,故不符合题意;
故选A.
【例5】(2021·广西中考真题)如图,已知抛物线与直线交于,两点,则关于的不等式的解集是( )
A.或 B.或 C. D.
【答案】D
【分析】
将要求的不等式抽象成两个函数的函数关系问题,根据二次函数图象的对称性,以及两一次函数图象的关系,求出新的一次函数与二次函数的交点,从而写出抛物线在直线上方部分的x的取值范围即可.
【详解】
与关于y轴对称
抛物线的对称轴为y轴,
因此抛物线与直线的交点和与直线的交点也关于y轴对称
设与交点为,则,
即在点之间的函数图像满足题意
的解集为:
故选D.
方法技巧
一元二次方程和二次函数的区别与联系
(1)求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.
(2)二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点和一元二次方程ax2+bx+c=0的根之间的关系:
Δ=b2-4ac决定抛物线与x轴的交点个数.
①Δ=b2-4ac>0时,抛物线与x轴有2个交点;
②Δ=b2-4ac=0时,抛物线与x轴有1个交点;
③Δ=b2-4ac<0时,抛物线与x轴没有交点.
(3)二次函数的交点式:y=a(x-x1)(x-x2)(a,b,c是常数,a≠0),可直接得到抛物线与x轴的交点坐标(x1,0),(x2,0).
针对训练
1.(2021·贵州中考真题)已知直线过一、二、三象限,则直线与抛物线的交点个数为( )
A.0个 B.1个 C.2个 D.1个或2个
【答案】C
【分析】
先由直线过一、二、三象限,求出,通过判断方程实数解的个数可判断直线与抛物线交点的个数.
【详解】
解:∵直线过一、二、三象限,
∴.
由题意得:,
即,
∵△,
∴此方程有两个不相等的实数解.
∴直线与抛物线的交点个数为2个.
故选:C.
2.(2021·黑龙江中考真题)已知函数,则下列说法不正确的个数是( )
①若该函数图像与轴只有一个交点,则
②方程至少有一个整数根
③若,则的函数值都是负数
④不存在实数,使得对任意实数都成立
A.0 B.1 C.2 D.3
【答案】C
【分析】
对于①:分情况讨论一次函数和二次函数即可求解;
对于②:分情况讨论a=0和a≠0时方程的根即可;
对于③:已知条件中限定a≠0且a>1或a<0,分情况讨论a>1或a<0时的函数值即可;
对于④:分情况讨论a=0和a≠0时函数的最大值是否小于等于0即可.
【详解】
解:对于①:当a=0时,函数变为,与只有一个交点,
当a≠0时,,∴,
故图像与轴只有一个交点时,或,①错误;
对于②:当a=0时,方程变为,有一个整数根为,
当a≠0时,方程因式分解得到:,其中有一个根为,故此时方程至少有一个整数根,故②正确;
对于③:由已知条件得到a≠0,且a>1或a<0
当a>1时,开口向上,对称轴为,自变量离对称轴越远,其对应的函数值越大,
∵ ,
∴离对称轴的距离一样,将代入得到,此时函数最大值小于0;
当a<0时,开口向下,自变量离对称轴越远,其对应的函数值越小,
∴时,函数取得最大值为,
∵a<0,
∴最大值,即有一部分实数,其对应的函数值,故③错误;
对于④:a=0时,原不等式变形为:对任意实数不一定成立,故a=0不符合;
a≠0时,对于函数,
当a>0时开口向上,总有对应的函数值,此时不存在a对对任意实数都成立;
当a<0时开口向下,此时函数的最大值为,
∵a<0,
∴最大值,即有一部分实数,其对应的函数值,
此时不存在a对对任意实数都成立;故④正确;
综上所述,②④正确,
故选:C.
3.(2021·广东中考真题)若一元二次方程(b,c为常数)的两根满足,则符合条件的一个方程为_____.
【答案】(答案不唯一)
【分析】
设与交点为,根据题意关于y轴对称和二次函数的对称性,可找到的值(只需满足互为相反数且满足即可)即可写出一个符合条件的方程
【详解】
设与交点为,
根据题意
则
的对称轴为
故设
则方程为:
故答案为:
考点4:求二次函数的解析式
1.二次函数的解析式的确定:
要确定二次函数的解析式,就是要确定解析式中的待定系数(常数)。
(1)当已知抛物线上任意三点时,通常将函数的解析式设为一般式;y=ax2+bx+c(a≠0);
(2)当已知抛物线的顶点坐标和抛物线上另一点时,通常将函数的解析式设为顶点式:y=a(x-h)2+k(a≠0).
(3)已知抛物线与x轴的两个交点的横坐标,一般选用交点式[y=a(x-x1)(x-x2)].
【例6】(2021·陕西中考真题)下表中列出的是一个二次函数的自变量x与函数y的几组对应值:
…
-2
0
1
3
…
…
6
-4
-6
-4
…
下列各选项中,正确的是( )
A.这个函数的图象开口向下 B.这个函数的图象与x轴无交点
C.这个函数的最小值小于-6 D.当时,y的值随x值的增大而增大
【答案】C
【分析】
利用表中的数据,求得二次函数的解析式,再配成顶点式,根据二次函数的性质逐一分析即可判断.
【详解】
解:设二次函数的解析式为,
依题意得:,解得:,
∴二次函数的解析式为=,
∵,
∴这个函数的图象开口向上,故A选项不符合题意;
∵,
∴这个函数的图象与x轴有两个不同的交点,故B选项不符合题意;
∵,∴当时,这个函数有最小值,故C选项符合题意;
∵这个函数的图象的顶点坐标为(,),
∴当时,y的值随x值的增大而增大,故D选项不符合题意;
故选:C.
方法技巧
根据已知条件确定二次函数的解析式,通常利用待定系数法.用待定系数法求二次函数的解析式必须根据题目的特点,选择适当的形式,才能使解题简便.一般来说,有如下几种情况:
(1)已知抛物线上三点的坐标,一般选用一般式(y=ax2+bx+c).
(2)已知抛物线顶点坐标或对称轴或最大(小)值,一般选用顶点式[y=a(x-h)2+k].
(3)已知抛物线与x轴的两个交点的横坐标,一般选用交点式[y=a(x-x1)(x-x2)].
(4)已知抛物线上纵坐标相同的两点,常选用顶点式:y=a(x-h)2+k(a≠0)
【方法解说】(1)若二次公数的图家经过三个已知点可没函数解析式为一般式,即y=ax2+bx+c;
(2)若知抛物线的顶点坐标,可出数解析式为顶点式,即y=a(x-h)2+k(a≠0),再根据抛物线与y轴的交点求出a的值;
(3)若抛物线与x轴的两个交点的坐标为(x1,0)和(x2,0),可没函数解析式为交点式,即y=a(x-x1)(x-x2),再根据抛物线与y轴的交点坐标求出a的值
针对训练
1.(2021·河南中考真题)请写出一个图象经过原点的函数的解析式__________.
【答案】y=x(答案不唯一)
【分析】
直接写出一个已经学过的经过原点的函数解析式即可.
【详解】
解:因为直线y=x经过原点(0,0),
故答案为:y=x(本题答案不唯一,只要函数图像经过原点即可).
2.(2021·浙江中考真题)在“探索函数的系数,,与图象的关系”活动中,老师给出了直角坐标系中的四个点:,,,,同学们探索了经过这四个点中的三个点的二次函数的图象,发现这些图象对应的函数表达式各不相同,其中的值最大为( )
A. B. C. D.
【答案】A
【分析】
分四种情况讨论,利用待定系数法,求过,,,中的三个点的二次函数解析式,继而解题.
【详解】
解:设过三个点,,的抛物线解析式为:
分别代入,,得
解得;
设过三个点,,的抛物线解析式为:
分别代入,,得
解得;
设过三个点,,的抛物线解析式为:
分别代入,,得
解得;
设过三个点,,的抛物线解析式为:
分别代入,,得
解得;
最大为,
故选:A.
3.(2021·广东中考真题)把抛物线向左平移1个单位长度,再向下平移3个单位长度,得到的抛物线的解析式为___.
【答案】
【分析】
直接根据“上加下减,左加右减”进行计算即可.
【详解】
解:抛物线向左平移1个单位长度,
再向下平移3个单位长度,
得到的抛物线的解析式为:,
即:
故答案为:.
考点5:二次函数的最值
【例7】(2021·广东中考真题)我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式,此公式与古希腊几何学家海伦提出的公式如出一辙,即三角形的三边长分别为a,b,c,记,则其面积.这个公式也被称为海伦-秦九韶公式.若,则此三角形面积的最大值为( )
A. B.4 C. D.5
【答案】C
【分析】
由已知可得a+b=6,,把b=6-a代入S的表达式中得:
,由被开方数是二次函数可得其最大值,从而可求得S的最大值.
【详解】
∵p=5,c=4,
∴a+b=2p-c=6
∴
由a+b=6,得b=6-a,代入上式,得:
设,当取得最大值时,S也取得最大值
∵
∴当a=3时,取得最大值4
∴S的最大值为
故选:C.针对训练
1.(2020•连云港)加工爆米花时,爆开且不糊的粒数的百分比称为“可食用率”.在特定条件下,可食用率y与加工时间x(单位:min)满足函数表达式y=﹣0.2x2+1.5x﹣2,则最佳加工时间为 min.
【分析】根据二次函数的性质可得.
【解析】根据题意:y=﹣0.2x2+1.5x﹣2,
当x=−1.52×(−0.2)=3.75时,y取得最大值,
则最佳加工时间为3.75min.
故答案为:3.75.
2.(2020•哈尔滨)抛物线y=3(x﹣1)2+8的顶点坐标为 .
【分析】已知抛物线顶点式y=a(x﹣h)2+k,顶点坐标是(h,k).
【解析】∵抛物线y=3(x﹣1)2+8是顶点式,
∴顶点坐标是(1,8).
故答案为:(1,8).
3.(2020•南京)小明和小丽先后从A地出发沿同一直道去B地.设小丽出发第xmin时,小丽、小明离B地的距离分别为y1m、y2m.y1与x之间的函数表达式是y1=﹣180x+2250,y2与x之间的函数表达式是y2=﹣10x2﹣100x+2000.
(1)小丽出发时,小明离A地的距离为 m.
(2)小丽出发至小明到达B地这段时间内,两人何时相距最近?最近距离是多少?
【分析】(1)根据题意和函数解析式,可以计算出小丽出发时,小明离A地的距离;
(2)根据题目中的函数解析式和题意,利用二次函数的性质,可以得到小丽出发至小明到达B地这段时间内,两人何时相距最近,最近距离是多少.
【解析】(1)∵y1=﹣180x+2250,y2=﹣10x2﹣100x+2000,
∴当x=0时,y1=2250,y2=2000,
∴小丽出发时,小明离A地的距离为2250﹣2000=250(m),
故答案为:250;
(2)设小丽出发第xmin时,两人相距sm,则
s=(﹣180x+2250)﹣(﹣10x2﹣100x+2000)=10x2﹣80x+250=10(x﹣4)2+90,
∴当x=4时,s取得最小值,此时s=90,
答:小丽出发第4min时,两人相距最近,最近距离是90m.
考点6:二次函数的应用
【例8】(2021·山东中考真题)公路上正在行驶的甲车,发现前方20m处沿同一方向行驶的乙车后,开始减速,减速后甲车行驶的路程s(单位:m)、速度v(单位:m/s)与时间t(单位:s) 的关系分别可以用二次函数和一次函数表示,其图象如图所示.
(1)当甲车减速至9m/s时,它行驶的路程是多少?
(2)若乙车以10m/s的速度匀速行驶,两车何时相距最近,最近距离是多少?
【答案】(1)87.5m;(2)6秒时两车相距最近,最近距离是2米
【分析】
(1)根据图像分别求出一次函数和二次函数解析式,令v=9求出t,代入求出s即可;
(2)分析得出当v=10m/s时,两车之间距离最小,代入计算即可.
【详解】
解:(1)由图可知:二次函数图像经过原点,
设二次函数表达式为,一次函数表达式为,
∵一次函数经过(0,16),(8,8),
则,解得:,
∴一次函数表达式为,
令v=9,则t=7,
∴当t=7时,速度为9m/s,
∵二次函数经过(2,30),(4,56),
则,解得:,
∴二次函数表达式为,
令t=7,则s==87.5,
∴当甲车减速至9m/s时,它行驶的路程是87.5m;
(2)∵当t=0时,甲车的速度为16m/s,
∴当10<v<16时,两车之间的距离逐渐变小,
当0<v<10时,两车之间的距离逐渐变大,
∴当v=10m/s时,两车之间距离最小,
将v=10代入中,得t=6,
将t=6代入中,得,
此时两车之间的距离为:10×6+20-78=2m,
∴6秒时两车相距最近,最近距离是2米.
针对训练
1.(2020•无锡)有一块矩形地块ABCD,AB=20米,BC=30米.为美观,拟种植不同的花卉,如图所示,将矩形ABCD分割成四个等腰梯形及一个矩形,其中梯形的高相等,均为x米.现决定在等腰梯形AEHD和BCGF中种植甲种花卉;在等腰梯形ABFE和CDHG中种植乙种花卉;在矩形EFGH中种植丙种花卉.甲、乙、丙三种花卉的种植成本分别为20元/米2、60元/米2、40元/米2,设三种花卉的种植总成本为y元.
(1)当x=5时,求种植总成本y;
(2)求种植总成本y与x的函数表达式,并写出自变量x的取值范围;
(3)若甲、乙两种花卉的种植面积之差不超过120平方米,求三种花卉的最低种植总成本.
【分析】(1)当x=5时,EF=20﹣2x=10,EH=30﹣2x=20,y=2×12(EH+AD)×20x+2×12(GH+CD)×x×60+EF•EH×40,即可求解;
(2)参考(1),由题意得:y=(30×30﹣2x)•x•20+(20+20﹣2x)•x•60+(30﹣2x)(20﹣2x)•40(0<x<10);
(3)S甲=2×12(EH+AD)×2x=(30﹣2x+30)x=﹣2x2+60x,S乙=﹣2x2+40x,则﹣2x2+60x﹣(﹣2x2+40x)≤120,即可求解.
【解析】(1)当x=5时,EF=20﹣2x=10,EH=30﹣2x=20,
y=2×12(EH+AD)×20x+2×12(GH+CD)×x×60+EF•EH×40=(20+30)×5×20+(10+20)×5×60+20×10×40=22000;
(2)EF=20﹣2x,EH=30﹣2x,
参考(1),由题意得:y=(30×30﹣2x)•x•20+(20+20﹣2x)•x•60+(30﹣2x)(20﹣2x)•40=﹣400x+24000(0<x<10);
(3)S甲=2×12(EH+AD)×2x=(30﹣2x+30)x=﹣2x2+60x,
同理S乙=﹣2x2+40x,
∵甲、乙两种花卉的种植面积之差不超过120米2,
∴﹣2x2+60x﹣(﹣2x2+40x)≤120,
解得:x≤6,
故0<x≤6,
而y=﹣400x+24000随x的增大而减小,故当x=6时,y的最小值为21600,
即三种花卉的最低种植总成本为21600元.
2.(2021·湖北中考真题)在“乡村振兴”行动中,某村办企业以,两种农作物为原料开发了一种有机产品,原料的单价是原料单价的1.5倍,若用900元收购原料会比用900元收购原料少.生产该产品每盒需要原料和原料,每盒还需其他成本9元.市场调查发现:该产品每盒的售价是60元时,每天可以销售500盒;每涨价1元,每天少销售10盒.
(1)求每盒产品的成本(成本=原料费+其他成本);
(2)设每盒产品的售价是元(是整数),每天的利润是元,求关于的函数解析式(不需要写出自变量的取值范围);
(3)若每盒产品的售价不超过元(是大于60的常数,且是整数),直接写出每天的最大利润.
【答案】(1)每盒产品的成本为30元.(2);(3)当时,每天的最大利润为16000元;当时,每天的最大利润为元.
【分析】
(1)设原料单价为元,则原料单价为元.然后再根据“用900元收购原料会比用900元收购原料少”列分式方程求解即可;
(2)直接根据“总利润=单件利润×销售数量”列出解析式即可;
(3)先确定的对称轴和开口方向,然后再根据二次函数的性质求最值即可.
【详解】
解:(1)设原料单价为元,则原料单价为元.
依题意,得.
解得,,.
经检验,是原方程的根.
∴每盒产品的成本为:(元).
答:每盒产品的成本为30元.
(2)
;
(3)∵抛物线的对称轴为=70,开口向下
∴当时,a=70时有最大利润,此时w=16000,即每天的最大利润为16000元;
当时,每天的最大利润为元.
中考数学一轮复习考点复习专题10 二次函数【考点精讲】(含解析): 这是一份中考数学一轮复习考点复习专题10 二次函数【考点精讲】(含解析),共26页。试卷主要包含了二次函数的一般形式,函数图象和性质等内容,欢迎下载使用。
初中数学中考复习 专题15 函数与行程问题【考点精讲】(解析版): 这是一份初中数学中考复习 专题15 函数与行程问题【考点精讲】(解析版),共16页。
初中数学中考复习 专题14 函数与利润问题【考点精讲】(解析版): 这是一份初中数学中考复习 专题14 函数与利润问题【考点精讲】(解析版),共22页。












