

初中数学中考复习 考点12 反比例函数的图像与性质及实际应用(解析版)
展开
这是一份初中数学中考复习 考点12 反比例函数的图像与性质及实际应用(解析版),共24页。
考点十二 反比例函数的图像与性质及实际应用
【命题趋势】
在中考中,反比例函数的图像与性质常以选择题和填空形式考查;反比例函数解析式主要在反比例函数综合题中与一次函数、几何图形结合考查。
【中考考查重点】
一、 结合具体情境体会反比例函数的意义,能根据已知条件确定反比例函数的表达式;
二、 能画出反比例函数的图像,根据图像和表达式探索并理解k>0和k<0时,图像的变化 情况;
三、 结合具体情境体会反比例函数的意义
四、 能用反比例函数解决简单实际问题
考点一:反比例函数的概念
概念
一般地,形如,叫做反比例函数,自变量x的取值范围是≠0的一切实数
【提分要点】反比例函数图像上的点的横纵坐标之积是定值k
1.(2021秋•南召县期末)下列函数是y关于x的反比例函数的是( )
A.y= B.y= C.y=﹣ D.y=﹣
【答案】C
【解答】解:A、不是y关于x的反比例函数,故此选项不合题意;
B、不是y关于x的反比例函数,故此选项不合题意;
C、是y关于x的反比例函数,故此选项符合题意;
D、不是y关于x的反比例函数,是正比例函数,故此选项不合题意;
故选C
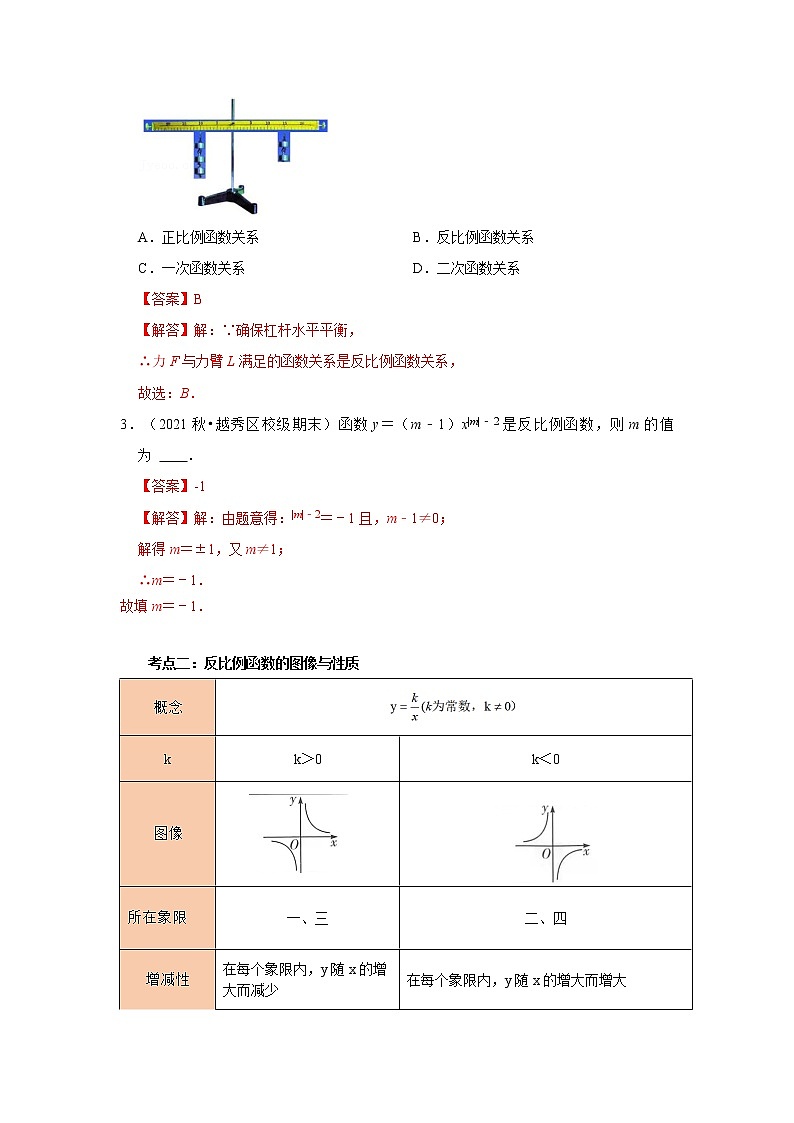
2.(2021•门头沟区一模)在物理实验室实验中,为了研究杠杆的平衡条件,设计了如下实验,如图,铁架台左侧钩码的个数与位置都不变,在保证杠杆水平平衡的条件下,右侧采取变动钩码数量即改变力F,或调整钩码位置即改变力臂L,确保杠杆水平平衡,则力F与力臂L满足的函数关系是( )
A.正比例函数关系 B.反比例函数关系
C.一次函数关系 D.二次函数关系
【答案】B
【解答】解:∵确保杠杆水平平衡,
∴力F与力臂L满足的函数关系是反比例函数关系,
故选:B.
3.(2021秋•越秀区校级期末)函数y=(m﹣1)x|m|﹣2是反比例函数,则m的值为 .
【答案】-1
【解答】解:由题意得:|m|﹣2=﹣1且,m﹣1≠0;
解得m=±1,又m≠1;
∴m=﹣1.
故填m=﹣1.
考点二:反比例函数的图像与性质
概念
k
k>0
k<0
图像
所在象限
一、三
二、四
增减性
在每个象限内,y随x的增大而减少
在每个象限内,y随x的增大而增大
图像特征
图像无限接近于坐标轴,但不与坐标轴相交;关于直线y=±x成轴对称;关于原点成中心对称
4.(2021秋•南开区期末)若反比例函数y=的图象在其所在的每一象限内,y随x的增大而减小,则k的取值范围是( )
A.k<﹣2 B.k>﹣2 C.k<2 D.k>2
【答案】B
【解答】解:∵反比例比例函数y=的图象在其每一象限内,y随x的增大而减小,
∴k+2>0,解得k>﹣2.
故选:B.
5.(2021秋•揭阳期末)点(x1,y1)、(x2,y2)、(x3,y3)在反比例函数y=﹣的图象上,且x1<0<x2<x3,则有( )
A.y1<y2<y3 B.y2<y3<y1 C.y1<y3<y2 D.y3<y2<y1
【答案】B
【解答】解:∵k<0,
∴函数图象在二,四象限,由x1<0<x2<x3可知,横坐标为x1的点在第二象限,横坐标为x2,x3的点在第四象限.
∵第四象限内点的纵坐标总小于第二象限内点的纵坐标,
∴y1最大,在第二象限内,y随x的增大而增大,
∴y2<y3<y1.
故选:B.
6.(2020秋•浦东新区校级期末)已知函数y=kx,y随x的增大而减小,另有函数,两个函数在同一平面直角坐标系内的大致图象可能是( )
A. B.
C. D.
【答案】B
【解答】解:∵函数y=kx中y随x的增大而减小,
∴k<0,且函数的图象经过第二、四象限,
∴函数的反比例系数大于零,
∴反比例函数图象经过第一、三象限,
故选:B.
7.(2020秋•孝义市期末)近视眼镜的度数y(度)与镜片焦距x(米)之间具有如图所示的反比例函数关系,若要配制一副度数小于400度的近视眼镜,则镜片焦距x的取值范围是( )
A.0米<x<0.25米 B.x>0.25米
C.0米<x<0.2米 D.x>0.2米
【答案】B
【解答】解:根据题意,近视眼镜的度数y(度)与镜片焦距x(米)成反比例,
设y=,
∵点(0.5,200)在此函数的图象上,
∴k=0.5×200=100,
∴y=(x>0),
∵y<400,
∴<400,
∵x>0,
∴400x>100,
∴x>0.25,
即镜片焦距x的取值范围是x>0.25米,
故选:B.
考点三:反比例函数系数k的几何意义
K的几何意义
在反比例函数上任取一点P(x,y),过这个点分别作x轴,y轴的垂线PM、PN,于坐标轴围成的矩形PMON的面积S=PM·PN===k
基本图形面积
基本图形面积
8.(2021秋•铁西区期末)如图,A是反比例函数y=的图象上一点,过点A作AB⊥y轴于点B,点C在x轴上,且S△ABC=2,则k的值为( )
A.4 B.﹣4 C.﹣2 D.2
【答案】B
【解答】解:设点A的坐标为(x,y),
∵点A在第二象限,
∴x<0,y>0,
∴S△ABC=AB•OB=|x|•|y|=﹣xy=2,
∴xy=﹣4,
∵A是反比例函数y=的图象上一点,
∴k=xy=﹣4,
故选:B.
9.(2021•铜仁市)如图,矩形ABOC的顶点A在反比例函数y=的图象上,矩形ABOC的面积为3,则k= .
【答案】3
【解答】解:∵矩形ABOC的面积为3,
∴|k|=3,
又∵k>0,
∴k=3,
故答案为:3.
考点四:反比例函数解析式的确定
待定系数法
1. 设所求反比例函数解析式为:
2. 找出反比例函数图像上一点P(a,b),并将其代入解析式得k=ab;
3. 确定反比例函数解析式
利用k得几何意义
题中已知面积时,考虑利用k得几何意义,由面积得,再综合图像所在象限判段k得正负,从而得出k的值,代入解析式即可
10.(2021秋•房山区期末)若反比例函数的图象经过点(3,﹣2),则该反比例函数的表达式为( )
A.y= B.y=﹣ C.y= D.y=﹣
【答案】B
【解答】解:设反比例函数的解析式为y=(k≠0),函数的图象经过点(3,﹣2),
∴﹣2=,得k=﹣6,
∴反比例函数解析式为y=﹣.
故选:B.
11.(2021秋•泰山区期中)如果等腰三角形的面积为6,底边长为x,底边上的高为y,则y与x的函数关系式为( )
A.y= B.y= C.y= D.y=
【答案】A
【解答】解:∵等腰三角形的面积为6,底边长为x,底边上的高为y,
∴xy=6,
∴y与x的函数关系式为:y=.
故选:A.
12.(2021•江西模拟)小明学习了物理中的杠杆平衡原理发现:阻力×阻力臂=动力×动力臂.现已知某一杠杆的阻力和阻力臂分别为2400N和1m,则动力F(单位:N)关于动力臂l(单位:m)的函数图象大致是( )
A. B.
C. D.
【答案】A
【解答】】解:∵阻力×阻力臂=动力×动力臂,已知阻力和阻力臂分别是2400N和1m,
∴动力F(单位:N)关于动力臂l(单位:m)的函数解析式为:2400×1=Fl,
则F=,是反比例函数,A选项符合,
故选:A.
1.(2021秋•隆回县期中)下面的函数是反比例函数的是( )
A.y= B.y= C.y= D.y=
【答案】C
【解答】解:A.y不是关于x的反比例函数,故本选项不符合题意;
B.y是x的是正比例函数,不是反比例函数,故本选项不符合题意;
C.y是关于x的反比例函数,故本选项符合题意;
D.y不是关于x的反比例函数,故本选项不符合题意;
故选:C.
2.(2021秋•大东区期末)如果反比例函数的图象经过点P(﹣3,﹣1),那么这个反比例函数的表达式为( )
A.y= B.y=﹣ C.y=x D.y=﹣x
【答案】A
【解答】解:设反比例函数解析式为y=(k≠0),
∵函数经过点P(﹣3,﹣1),
∴﹣1=,
解得k=3.
∴反比例函数解析式为y=.
故选:A.
3.(2021春•海淀区校级月考)某物体对地面的压力为定值,物体对地面的压强p(Pa)与受力面积S(m2)之间的函数关系如图所示,这一函数表达式为( )
A. B. C. D.
【答案】B
【解答】解:观察图象易知p与S之间的是反比例函数关系,设p=,
由于A(20,10)在此函数的图象上,
∴k=20×10=200,
∴p=.
故选:B.
4.(2020秋•瓜州县期末)如图,在某温度不变的条件下,通过一次又一次地对气缸顶部的活塞加压,测出每一次加压后气缸内气体的体积V(mL)与气体对气缸壁产生的压强p(kPa)的关系可以用如图所示的反比例函数图象进行表示,下列说法错误的是( )
A.气压p与体积V表达式为p=,则k>0
B.当气压p=70时,体积V的取值范围为70<V<80
C.当体积V变为原来的时,对应的气压p变为原来的
D.当60≤V≤100时,气压p随着体积V的增大而减小
【答案】B
【解答】解:当V=60时,p=100,则pV=6000,
A.气压p与体积V表达式为p=,则k>0,故不符合题意;
B.当p=70时,V=>80,故符合题意;
C.当体积V变为原来的时,对应的气压p变为原来的,不符合题意;
D.当60≤V≤100时,气压p随着体积V的增大而减小,不符合题意;
故选:B.
5.(2020秋•东莞市校级期末)已知点(3,y1),(﹣2,y2),(2,y3)都在反比例函数的图象上,那么y1,y2与y3的大小关系是( )
A.y3<y1<y2 B.y3<y2<y1 C.y1<y2<y3 D.y1<y3<y2
【答案】A
【解答】解:∵k=﹣6<0,
∴图象位于第二、四象限,在每一象限内,y随x的增大而增大,
∴y2>0,y3<y1<0,
∴y3<y1<y2,
故选:A.
6.(2021秋•西湖区期中)已知y1和y2均是以x为自变量的函数,当x=m时,函数值分别是M1和M2,若存在实数m,使得M1+M2=1,则称函数y1和y2具有性质P.以下函数y1和y2不具有性质P的是( )
A.y1=x2+2x和y2=﹣x﹣1 B.y1=x2+2x和y2=﹣x+1
C.y1=﹣和y2=﹣x﹣1 D.y1=﹣和y2=﹣x+1
【答案】D
【解答】解:A.令y1+y2=1,则x2+2x﹣x﹣1=1,整理得,x2+x﹣2=0,解得x=﹣2或x=1,即函数y1和y2具有性质P,不符合题意;
B.令y1+y2=1,则x2+2x﹣x+1=1,整理得,x2+x=0,解得x=0或x=﹣1,即函数y1和y2具有性质P,不符合题意;
C.令y1+y2=1,则﹣﹣x﹣1=1,整理得,x2+2x+1=0,解得x1=x2=﹣1,即函数y1和y2具有性质P,不符合题意;
D.令y1+y2=1,则﹣﹣x+1=1,整理得,x2+1=0,方程无解,即函数y1和y2不具有性质P,符合题意;
故选:D.
7.(2021秋•会宁县期末)如图,A,B是反比例函数的图象上关于原点对称的两点,BC∥x轴,AC∥y轴,若△ABC的面积为6,则k的值是 .
【答案】3
【解答】解:∵反比例函数的图象在一、三象限,
∴k>0,
∵BC∥x轴,AC∥y轴,
∴S△AOD=S△BOE=k,
∵反比例函数及正比例函数的图象关于原点对称,
∴A、B两点关于原点对称,
∴S矩形OECD=2S△AOD=k,
∴S△ABC=S△AOD+S△BOE+S矩形OECD=2k=6,解得k=3.
故答案为:3.
8.(2021春•沙坪坝区校级期末)已知函数y=(m﹣1)是反比例函数,则m的值为 .
【答案】-1
【解答】解:根据题意m2﹣2=﹣1,
∴m=±1,
又m﹣1≠0,m≠1,
所以m=﹣1.
故答案为:﹣1.
1.(2018•柳州)已知反比例函数的解析式为y=,则a的取值范围是( )
A.a≠2 B.a≠﹣2 C.a≠±2 D.a=±2
【答案】C
【解答】解:根据反比例函数解析式中k是常数,不能等于0,由题意可得:|a|﹣2≠0,
解得:a≠±2,
故选:C.
2.(2020•上海)已知反比例函数的图象经过点(2,﹣4),那么这个反比例函数的解析式是( )
A.y= B.y=﹣ C.y= D.y=﹣
【答案】D
【解答】解:设反比例函数解析式为y=,
将(2,﹣4)代入,得:﹣4=,
解得k=﹣8,
所以这个反比例函数解析式为y=﹣,
故选:D.
3.(2021•黔西南州)对于反比例函数y=,下列说法错误的是( )
A.图象经过点(1,﹣5)
B.图象位于第二、第四象限
C.当x<0时,y随x的增大而减小
D.当x>0时,y随x的增大而增大
【答案】C
【解答】解:∵反比例函数y=,
∴当x=1时,y=﹣=﹣5,故选项A不符合题意;
k=﹣5,故该函数图象位于第二、四象限,故选项B不符合题意;
当x<0,y随x的增大而增大,故选项C符合题意;
当x>0时,y随x的增大而增大,故选项D不符合题意;
故选:C.
4.(2021•济南)反比例函数y=(k≠0)图象的两个分支分别位于第一、三象限,则一次函数y=kx﹣k的图象大致是( )
A. B. C. D.
【答案】D
【解答】解:∵反比例函数y=(k≠0)图象的两个分支分别位于第一、三象限,
∴k>0,
∴﹣k<0,
∴一次函数y=kx﹣k的图象图象经过第一、三、四象限,
故选:D.
5.(2021•宜昌)某气球内充满了一定质量m的气体,当温度不变时,气球内气体的气压p(单位:kPa)是气体体积V(单位:m3)的反比例函数:p=,能够反映两个变量p和V函数关系的图象是( )
A. B.
C. D.
【答案】B
【解答】解:∵气球内气体的气压p(单位:kPa)是气体体积V(单位:m3)的反比例函数:p=(V,p都大于零),
∴能够反映两个变量p和V函数关系的图象是:.
故选:B.
6.(2021•沈阳)如图,平面直角坐标系中,O是坐标原点,点A是反比例函数y=(k≠0)图象上的一点,过点A分别作AM⊥x轴于点M,AN⊥y轴于点N.若四边形AMON的面积为12,则k的值是 .
【答案】-12
【解答】解:∵四边形AMON的面积为12,
∴|k|=12,
∵反比例函数图象在二四象限,
∴k<0,
∴k=﹣12,
故答案为:﹣12.
7.(2021•阜新)已知点A(x1,y1),B(x2,y2)都在反比例函数y=﹣的图象上,且x1<0<x2,则y1,y2的关系一定成立的是( )
A.y1>y2 B.y1<y2 C.y1+y2=0 D.y1﹣y2=0
【答案】A
【解答】解:∵反比例函数y=﹣中k=﹣1<0,
∴函数图象的两个分支分别位于二、四象限,且在每一象限内,y随x的增大而增大.
∵x1<0<x2,
∴A在第二象限,B在第四象限,
∴y1>0,y2<0,
∴y1>y2.
故选:A.
8.(2020•大庆)已知正比例函数y=k1x和反比例函数y=,在同一平面直角坐标系下的图象如图所示,其中符合k1•k2>0的是( )
A.①② B.①④ C.②③ D.③④
【答案】B
【解答】解:①中k1>0,k2>0,故k1•k2>0,故①符合题意;
②中k1<0,k2>0,故k1•k2<0,故②不符合题意;
③中k1>0,k2<0,故k1•k2<0,故③不符合题意;
④中k1<0,k2<0,故k1•k2>0,故④符合题意;
故选:B.
9.(2021•自贡)已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.下列说法正确的是( )
A.函数解析式为I= B.蓄电池的电压是18V
C.当I≤10A时,R≥3.6Ω D.当R=6Ω时,I=4A
【答案】C
【解答】解:设I=,
∵图象过(4,9),
∴k=36,
∴I=,
∴蓄电池的电压是36V.
∴A,B均错误;
当I=10时,R=3.6,
由图象知:当I≤10A时,R≥3.6Ω,
∴C正确,符合题意;
当R=6时,I=6,
∴D错误,
故选:C.
10.(2020•河北)如图是8个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作Tm(m为1~8的整数).函数y=(x<0)的图象为曲线L.
(1)若L过点T1,则k= ;
(2)若L过点T4,则它必定还过另一点Tm,则m= ;
(3)若曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,则k的整数值有 个.
【答案】(1)-16 (2)5 (3)7
【解答】解:(1)∵每个台阶的高和宽分别是1和2,
∴T1(﹣16,1),T2(﹣14,2),T3(﹣12,3),T4(﹣10,4),T5(﹣8,5),T6(﹣6,6),T7(﹣4,7),T8(﹣2,8),
∵L过点T1,
∴k=﹣16×1=﹣16,
故答案为:﹣16;
(2)∵L过点T4,
∴k=﹣10×4=﹣40,
∴反比例函数解析式为:y=﹣,
当x=﹣8时,y=5,
∴T5在反比例函数图象上,
∴m=5,
故答案为:5;
(3)若曲线L过点T1(﹣16,1),T8(﹣2,8)时,k=﹣16,
若曲线L过点T2(﹣14,2),T7(﹣4,7)时,k=﹣14×2=﹣28,
若曲线L过点T3(﹣12,3),T6(﹣6,6)时,k=﹣12×3=﹣36,
若曲线L过点T4(﹣10,4),T5(﹣8,5)时,k=﹣40,
∵曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,
∴﹣36<k<﹣28,
∴整数k=﹣35,﹣34,﹣33,﹣32,﹣31,﹣30,﹣29共7个,
故答案为:7.
声明:试题解析著作权属所有,未经书面同意,不得复制发布
1.(2021•抚顺模拟)下列函数中,y是x的反比例函数的是( )
A. B. C. D.
【答案】B
【解答】解:A、是正比例函数,不是反比例函数,故此选项不合题意;
B、是反比例函数,故此选项符合题意;
C、不是反比例函数,故此选项不合题意;
D、不是反比例函数,故此选项不合题意;
故选:B.
2.(2021•卧龙区二模)已知反比例函数,在下列结论中,不正确的是( )
A.图象必经过点(﹣1,﹣2)
B.图象在第一、三象限
C.若x<﹣1,则y<﹣2
D.点A(x1,y1),B(x2,y2)图象上的两点,且x1<0<x2,则y1<y2
【答案】C
【解答】解:A.反比例函数,图象必经过点(﹣1,﹣2),原说法正确,故此选项不合题意;
B.反比例函数,图象在第一、三象限,原说法正确,故此选项不合题意;
C.若x<﹣1,则y>﹣2,原说法错误,故此选项符合题意;
D.点A(x1,y1),B(x2,y2)图象上的两点,且x1<0<x2,则y1<y2,原说法正确,故此选项不合题意;
故选:C.
3.(2021•富阳区二模)已知反比例函数y=,当﹣2<x<﹣1,则下列结论正确的是( )
A.﹣3<y<0 B.﹣2<y<﹣1 C.﹣10<y<﹣5 D.y>﹣10
【答案】C
【解答】解:∵k=10,且﹣2<x<﹣1,
∴在第三象限内,y随x的增大而减小,
当x=﹣2时,y=﹣5,
当x=﹣1时,y=﹣10,
∴﹣10<y<﹣5,
故选:C.
4.(2021•武陟县模拟)某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kpa)是气体体积V(m3)的反比例函数其图象如图所示,当气体体积为1m3时,气压为( )kPa.
A.150 B.120 C.96 D.84
【答案】C
【解答】解:设P=,
由题意知120=,
所以k=96,
故P=,
当V=1m3时,P==96(kPa);
故选:C.
5.(2021•云岩区模拟)阿基米德说:“给我一个支点,我就能撬动整个地球”这句话精辟地阐明了一个重要的物理学知识﹣﹣杠杆原理,即“阻力×阻力臂=动力×动力臂”.若已知某一杠杆的阻力和阻力臂分别为1200N和0.5m,则这一杠杆的动力F和动力臂l之间的函数图象大致是( )
A. B.
C. D.
【答案】A
【解答】解:∵阻力×阻力臂=动力×动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1200N和0.5m,
∴动力F(单位:N)关于动力臂l(单位:m)的函数解析式为:1200×0.5=Fl,
则F=,是反比例函数,A选项符合,
故选:A.
6.(2021•昆明模拟)如图,点P在双曲线第一象限的图象上,PA⊥x轴于点A,则△OPA的面积为( )
A.2 B.3 C.4 D.6
【答案】B
【解答】解:∵PA⊥x轴于点A,
∴S△AOP=|k|==3,
故选:B.
7.(2021•乐陵市一模)为预防新冠病毒,某学校每周末用药熏消毒法对教室进行消毒,已知药物释放过程中,教室内每立方米空气中含药量y(mg)与时间t(h)成正比例;药物释放完毕后,y与t成反比例,如图所示.根据图象信息,下列选项错误的是( )
A.药物释放过程需要小时
B.药物释放过程中,y与t的函数表达式是y=t
C.空气中含药量大于等于0.5mg/m3的时间为h
D.若当空气中含药量降低到0.25mg/m3以下时对身体无害,那么从消毒开始,至少需要经过4.5小时学生才能进入教室
【答案】D
【解答】解:设正比例函数解析式是y=kt,
反比例函数解析式是y=,
把点(3,)代入反比例函数的解析式,得:=,
解得:m=,
∴反比例函数的解析式是y=.
当y=1时,代入上式得t=,
把t=时,y=1代入正比例函数的解析式是y=kt,得:k=,
∴正比例函数解析式是y=t,
A.由图象知,y=1时,t=,即药物释放过程需要小时,故A不符合题意;
B.药物释放过程中,y与t成正比例,函数表达式是y=t,故B不符合题意;
C.把y=0.5mg/m3分别代入y=t和y=得,0.5=t1和0.5=,
解得:t1=和t2=3,
∴t2﹣t1=,
∴空气中含药量大于等于0.5mg/m3的时间为h;故C不符合题意;
<0.25,
解得t>6,
所以至少需要经过6小时后,学生才能进入教室,故D符合题意,
故选:D.
8.(2021•山西模拟)已知,A(﹣3,n),C(3n﹣6,2)是反比例函数y=(x<0)图象上的两点,则反比例函数的解析式为 .
【答案】y=﹣
【解答】解:∵A(﹣3,n),C(3n﹣6,2)是反比例函数y=(x<0)图象上的两点,
∴n=,2=,即m=﹣3n,m=2(3n﹣6),
消去m得:﹣3n=2(3n﹣6),
解得:n=,
把n=代入得:m=﹣4,
则反比例函数解析式为y=﹣.
故答案为:y=﹣.
9.(2021•雁塔区校级模拟)已知同一象限内的两点A(3,n),B(n﹣4,n+3)均在反比例函数y=的图象上,则该反比例函数关系式为 .
【答案】y=
【解答】解:∵同一象限内的两点A(3,n),B(n﹣4,n+3)均在反比例函数y=的图象上,
∴k=3n=(n﹣4)(n+3),
解得n=6或n=﹣2,
∵n=﹣2时,A(3,﹣2),B(﹣6,1),
∴A、B不在同一象限,故n=﹣2舍去,
∵k=3n=18,
∴y=,
故答案为y=.
10.(2021•昭通模拟)若函数y=是关于x的反比例函数,则a满足的条件是 .
【答案】a≠﹣3
【解答】解:由题可得,a+3≠0,
解得a≠﹣3,
故答案为:a≠﹣3.
相关试卷
这是一份中考数学一轮复习知识点梳理+练习考点12 反比例函数的图像与性质及实际应用(含解析),共1页。
这是一份(通用版)中考数学一轮复习考点练习12 反比例函数的图像与性质及实际应用(教师版),共1页。
这是一份初中数学中考复习 考点24 解直角三角形的实际应用(解析版),共28页。








