

初中数学中考复习 考点24 解直角三角形的实际应用(解析版)
展开考点二十四 解直角三角形的实际应用
【命题趋势】
在中考中,锐角三角形函数主要选择题、填空题,解答题考查为主,难度系数低。
【中考考查重点】
解直角三角形的实际应用
1.解一个直角三角形
2.背靠背型
3.母子型
考点 解直角三角形的实际应用
类型一 仰角、俯角
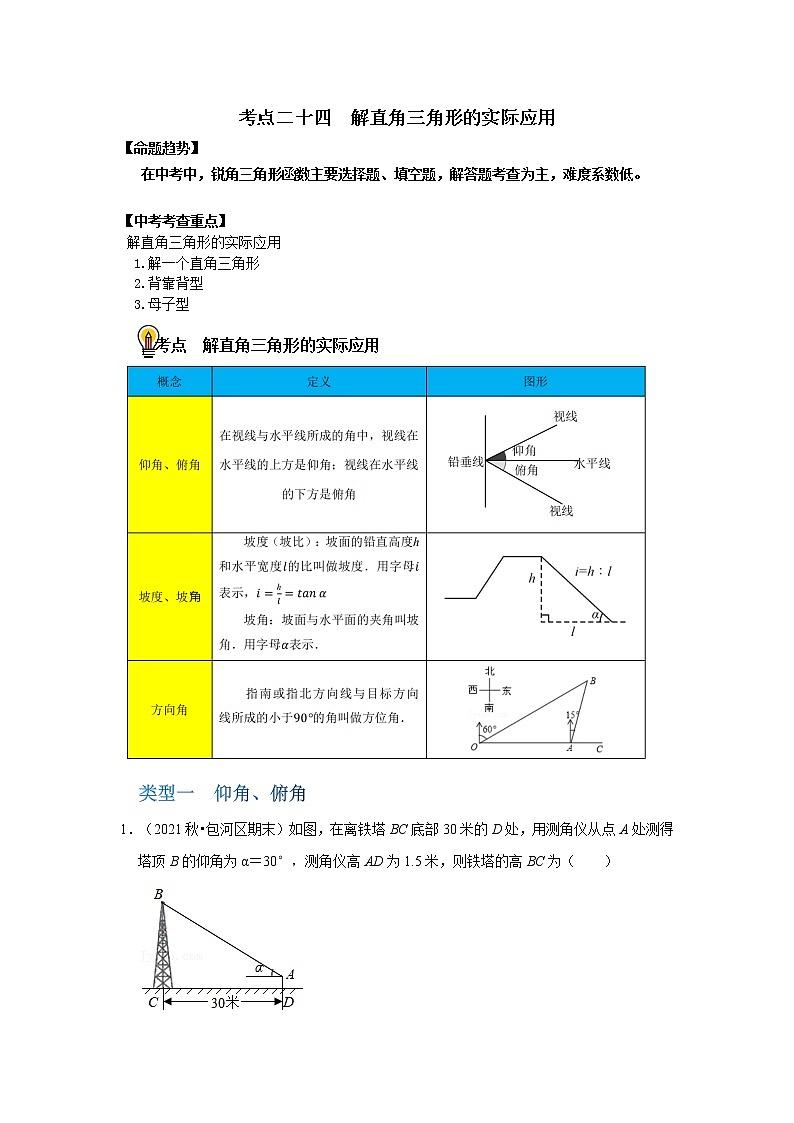
1.(2021秋•包河区期末)如图,在离铁塔BC底部30米的D处,用测角仪从点A处测得塔顶B的仰角为α=30°,测角仪高AD为1.5米,则铁塔的高BC为( )
A.16.5米 B.(10+1.5)米
C.(15+1.5)米 D.(15+1.5)米
【答案】B
【解答】解:过点A作AE⊥BC,E为垂足,如图所示:
则四边形ADCE为矩形,AE=30米,
∴CE=AD=1.5米,
在Rt△ABE中,tanα==tan30°=,
∴BE=AE=×30=10(米),
∴BC=BE+CE=(10+1.5)米,
故选:B.
2.(2021秋•丛台区校级期末)如图,小东在教学楼距地面8米高的窗口C处,测得正前方旗杆顶部A点的仰角为37°,旗杆底部B点的俯角为45°,升旗时,国旗上端悬挂在距地面2.5米处,若国旗随国歌声冉冉升起,并在国歌播放46秒结束时到达旗杆顶端,则国旗匀速上升的速度为( )米/秒.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A.0.3 B.0.2 C.0.25 D.0.35
【答案】C
【解答】解:在Rt△BCD中,BD=8米,∠BCD=45°,
∴△BCD是等腰直角三角形,
∴BD=CD=8米,
在Rt△ACD中,CD=8米,∠ACD=37°,
∴AD=CD•tan37°≈8×0.75=6(米),
∴旗杆AB的高为:AD+BD=6+8=14(米);
升旗时,国旗上升高度是:14﹣2.5=11.5(米),
∵耗时46s,
∴国旗匀速上升的速度为:=0.25(米/秒),
故选:C.
3.(2021秋•历城区期末)如图,某建筑物的顶部有一块宣传牌CD,小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°,已知斜坡AB的坡角为30°,AB=10米,AE=15米,则宣传牌CD的高度是( )
A. B. C. D.
【答案】A
【解答】解:过B作BF⊥AE,交EA的延长线于F,作BG⊥DE于G.
在Rt△ABF中,∠BAF=30°,AB=10米,
∴BF=AB=5(米),AF=BF=5(米).
∴BG=AF+AE=(5+15)(米),
在Rt△BGC中,∠CBG=45°,
∴△BGC是等腰直角三角形,
∴CG=BG=(5+15)(米),
在Rt△ADE中,∠DAE=60°,AE=15米,
∴DE=AE=15(米),
∴CD=CG+GE﹣DE=5+15+5﹣15=(20﹣10)(米),
即宣传牌CD的高度是(20﹣10)米,
故选:A.
4.(2021秋•汉寿县期末)如图,某办公楼AB的后面有一建筑物CD(办公楼AB与建筑物CD均垂直于地面BCF),当光线与地面的夹角是22°时,办公楼在建筑物CD的墙上留下的影子CE=2米,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有25米的距离(点B,F,C在同一条直线上).
(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:sin22°≈,cos22°≈,tan22°≈,)
【答案】(1) 20m (2)48米
【解答】解:(1)过点E作EM⊥AB于点M,
则四边形BCEM为矩形,
∴BM=CE=2米,
设AB=x米,
在Rt△ABF中,∠AFB=45°,
∴BF=AB=x米,
∴BC=BF+FC=(x+25)米,AM=(x﹣2)米,
在Rt△AEM中,tan∠AEM=,
则≈,
解得:x=20,
答:办公楼AB的高度为20m;
(2)在Rt△AME中,cos∠AEM=,
则cos22°=,即≈,
解得:AE=48,
答:A,E之间的距离约为48米.
类型二 坡度、坡角
5.(2021秋•淇县期末)如图,河坝横断面迎水坡AB的坡比为1:,坝高BC=3m,则AC的长度为( )
A.6m B.m C.9m D.m
【答案】D
【解答】解:∵坡AB的坡比为1:,
∴BC:AC=1:,
∵BC=3m,
∴AC=3m,
故选:D.
16.(2021秋•莱芜区期末)如图,某水库大坝的横断面是梯形ABCD,坝高DE=5m,斜坡BC的坡比为5:12,则斜坡BC=( )
A.13m B.8m C.18m D.12m
【答案】A
【解答】解:过点C作CF⊥AB于F,
∵DC∥AB,
∴CF=DE=5m,
∵斜坡BC的坡比为5:12,CF=5m,
∴BF=12m,
由勾股定理得:BC===13(m),
故选:A.
6.(2021秋•龙口市期末)如图,山区某教学楼后面紧邻着一个土坡,坡面BC平行于地面AD,斜坡AB的坡比为i=1:,且AB=26米,为了防止山体滑坡,保障安全,学校决定对该土坡进行改造,经地质人员勘测,当坡角不超过53°时,可确保山体不滑坡;
(1)求改造前坡顶与地面的距离BE的长;
(2)为了消除安全隐患,学校计划将斜坡AB改造成AF(如图所示),那么BF至少是多少米?(结果精确到1米)
【参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75】
【答案】(1) BE=24 (2)BE为24米;BF至少是8米
【解答】解:(1)在Rt△ABE中,AB=26,i==,
设BE=12k,AE=5k,则AB=13k=26,k=2,
∴AE=10(米),BE=24(米);
(2)过点F作FG⊥AD于点G,
由题意可知:FG=BE=24,∠FAD=53°,
在Rt△AFG中,cot53°==0.75,
∴AG=18(米),
∴BF=GE=AG﹣AE=8(米),
答:改造前坡顶与地面的距离BE为24米;BF至少是8米.
类型三 方向角
7.(2021秋•汝阳县期末)如图,点A到点C的距离为100米,要测量河对岸B点到河岸AD的距离.小明在A点测得B在北偏东60°的方向上,在C点测得B在北偏东30°的方向上,则B点到河岸AD的距离为( )
A.100米 B.50米 C.米 D.50米
【答案】D
【解答】解:过B作BM⊥AD于M,如图:
由题意得:∠BAD=90°﹣60°=30°,∠BCD=90°﹣30°=60°,
∴∠ABC=∠BCD﹣∠BAD=30°,
∴∠BAD=∠ABC,
∴BC=AC=100米,
∵BM⊥AD,
∴∠BMC=90°,
在Rt△BCM中,sin∠BCM=,
∴BM=BC×sin∠BCM=100×=50(米),
即B点到河岸AD的距离为50米,
故选:D.
8.(2021•钦州模拟)如图,一艘测量船在A处测得灯塔S在它的南偏东60°方向,测量船继续向正东航行30海里后到达B处,这时测得灯塔S在它的南偏西75°方向,则灯塔S离观测点A的距离是( )
A.15海里 B.(15﹣15)海里
C.(15﹣15)海里 D.15海里
【答案】B
【解答】解:过S作SC⊥AB于C,在AB上截取CD=AC,
∴AS=DS,
∴∠CDS=∠CAS=30°,
∵∠ABS=15°,
∴∠DSB=15°,
∴SD=BD,
设CS=x海里,
在Rt△ASC中,∠CAS=30°,
∴AC=x(海里),AS=DS=BD=2x(海里),
∵AB=30海里,
∴x+x+2x=30,
解得:x=,
∴AS=(15﹣15)(海里),
故选:B.
9.(2021秋•成武县期中)如图在某监测点B处望见一艘正在作业的渔船在南偏西15方向的A处,若渔船沿北偏西75°方向以60海里/小时的速度航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B、C之间的距离为( )
A.30海里 B.20海里 C.20海里 D.30海里
【答案】D
【解答】解:如图,由题意得:AC=60×0.5=30(海里),
∵CD∥BF,
∴∠CBF=∠DCB=60°,
∵∠ABF=15°,
∴∠ABC=∠CBF﹣∠ABF=45°,
∵AE∥BF,
∴∠EAB=∠FBA=15°,
又∵∠EAC=75°,
∴∠CAB=∠EAB+∠EAC=90°,
∴△ABC是等腰直角三角形,
∴BC=AC=30(海里),
故选:D.
1.(2021秋•历下区期末)我国航天事业捷报频传,天舟二号于2021年5月29日成功发射,震撼人心.当天舟二号从地面到达点A处时,在P处测得A点的仰角∠DPA为30°,A与P两点的距离为10千米;它沿铅垂线上升到达B处时,此时在P处测得B点的仰角∠DPB为45°,则天舟二号从A处到B处的距离AB的长为( )(参考数据:≈1.7,≈1.4).
A.2.0千米 B.1.5千米 C.2.5千米 D.3.5千米
【答案】D
【解答】解:在Rt△APD中,∠DPA=30°,AP=10千米,∠ADP=90°,cos∠DPA=cos30°=,
∴AD=AP=×10=5(千米),PD=AP•cos30°=10×=5(千米),
在Rt△BPD中,tan∠DPB=tan45°=,
∴BD=PD•tan45°=5×1=5(千米),
∴AB=BD﹣AD=5﹣5≈8.5﹣5=3.5(千米),
故选:D.
2.(2021秋•盐湖区期末)如图,一艘轮船在小岛A的西北方向距小岛40海里的C处,沿正东方向航行一段时间后到达小岛A的北偏东60°的B处,则该船行驶的路程为( )
A.80海里 B.120海里
C.(40+40)海里 D.(40+40)海里
【答案】D
【解答】解:如图,过点A作AD⊥BC于D,
由题意得,∠CAD=45°,∠BAD=60°,AC=40海里,
在Rt△ADC中,∠ADC=90°,∠CAD=45°,AC=40海里,
∴AD=CD=×40=40(海里),
在Rt△ADB中,∠ADB=90°,∠BAD=45°,AD=40海里,
∴BD=AD=40(海里),
∴BC=CD+BD=(40+40)海里,
故选:D.
3.(2021秋•柯城区期末)如图,河坝横断面迎水坡AB的坡比是1:2(坡比是坡面铅直高度BC与水平宽度AC之比),坝高BC=3m,则坡面AB的长度最接近( )(参考数据:≈1.73,≈2.24)
A.5.2m B.6m C.6.7m D.9m
【答案】C
【解答】解:∵坡AB的坡比是1:2,BC=3m,
∴AC=6cm,
由勾股定理得:AB===3≈6.7(m),
故选:C.
4.(2021秋•通州区期末)如图,要测量山高CD,可以把山坡“化整为零”地划分为AB和BC两段,每一段上的山坡近似是“直”的.若量得坡长AB=600m,BC=800m,测得坡角∠BAD=30°,∠CBE=45°,则山高CD为( )
A.(300+800)m B.700m
C.(300+400)m D.(400+300)m
【答案】C
【解答】解:由题意可知,四边形BFDE为矩形,
∴DE=BF,
在Rt△BAF中,∠BAF=30°,AB=600m,
则BF=AB=300(m),
∴DE=300m,
在Rt△CBE中,∠CBE=45°,BC=800m,
∴CE=BC=400(m),
∴CD=CE+DE=(300+400)m,
故选:C.
5.(2021秋•安居区期末)如图所示,某拦水大坝的横断面为梯形ABCD,AE,DF为梯形的高,其中迎水坡AB的坡角α=45°,坡长AB=10米,背水坡CD的坡度i=1:,则背水坡的坡长CD为( )米.
A.20 B.20 C.10 D.20
【答案】A
【解答】解:由题意得:四边形AEFD是矩形,
∴DF=AE,
∵迎水坡AB的坡角α=45°,坡长AB=10米,
∴DF=AE=10×sin45°=10(米),
∵背水坡CD的坡度i=1:,
∴tanC=i===,
∴∠C=30°,
∴CD=2DF=2AE=20(米),
故选:A.
6.(2021秋•临淄区期末)为了学生的安全,某校决定把一段如图所示的步梯路段进行改造.已知四边形ABCD为矩形,DE=10m,其坡度为i1=1:,将步梯DE改造为斜坡AF,其坡度为i2=1:4,求斜坡AF的长度是 米.(结果精确到0.01m,参考数据:≈1.732,≈4.123)
【答案】20.62
【解答】解:∵DE的坡度为i1=1:,
∴tan∠DEC==,
∴∠DEC=30°,
∴DC=DE=5(m),
∵四边形ABCD为矩形,
∴AB=CD=5m,
∵斜坡AF的坡度为i2=1:4,AB=5m,
∴BF=4AB=20(m),
在Rt△ABF中,AF==≈20.62(m),
∴斜坡AF的长度约为20.62米,
故答案为:20.62.
7.(2021•抚顺)某景区A、B两个景点位于湖泊两侧,游客从景点A到景点B必须经过C处才能到达.观测得景点B在景点A的北偏东30°,从景点A出发向正北方向步行600米到达C处,测得景点B在C的北偏东75°方向.
(1)求景点B和C处之间的距离;(结果保留根号)
(2)当地政府为了便捷游客游览,打算修建一条从景点A到景点B的笔直的跨湖大桥.大桥修建后,从景点A到景点B比原来少走多少米?(结果保留整数.参考数据:≈1.414,≈1.732)
【答案】(1)300m (2)205m
【解答】解:(1)过点C作CD⊥AB于点D,
由题意得,∠A=30°,∠BCE=75°,AC=600m,
在Rt△ACD中,∠A=30°,AC=600,
∴CD=AC=300(m),
AD=AC=300(m),
∵∠BCE=75°=∠A+∠B,
∴∠B=75°﹣∠A=45°,
∴CD=BD=300(m),
BC=CD=300(m),
答:景点B和C处之间的距离为300m;
(2)由题意得.
AC+BC=(600+300)m,
AB=AD+BD=(300+300)m,
AC+BC﹣AB=(600+300)﹣(300+300)
≈204.6
≈205(m),
答:大桥修建后,从景点A到景点B比原来少走约205m.
1.(2021•深圳)如图,在点F处,看建筑物顶端D的仰角为32°,向前走了15米到达点E即EF=15米,在点E处看点D的仰角为64°,则CD的长用三角函数表示为( )
A.15sin32° B.15tan64° C.15sin64° D.15tan32°
【答案】C
【解答】解:∵∠CED=64°,∠F=32°,∠CED=∠F+∠EDF,
∴∠EDF=∠CED﹣∠F=64°﹣32°=32°,
∴∠EDF=∠F,
∴DE=EF,
∵EF=15米,
∴DE=15米,
在Rt△CDE中,
∵sin∠CED=,
∴CD=DEsin∠CED=15sin64°,
故选:C.
2.(2021•重庆)如图,在建筑物AB左侧距楼底B点水平距离150米的C处有一山坡,斜坡CD的坡度(或坡比)为i=1:2.4,坡顶D到BC的垂直距离DE=50米(点A,B,C,D,E在同一平面内),在点D处测得建筑物顶点A的仰角为50°,则建筑物AB的高度约为( )
(参考数据:sin50°≈0.77;cos50°≈0.64;tan50°≈1.19)
A.69.2米 B.73.1米 C.80.0米 D.85.7米
【答案】D
【解答】解:∵斜坡CD的坡度(或坡比)为i=1:2.4,
∴DE:CE=5:12,
∵DE=50米,
∴CE=120米,
∵BC=150米,
∴BE=150﹣120=30(米),
∴AB=tan50°×30+50
≈85.7(米).
故选:D.
3.(2020•自贡)如图,我市在建高铁的某段路基横断面为梯形ABCD,DC∥AB.BC长6米,坡角β为45°,AD的坡角α为30°,则AD长为 米(结果保留根号).
【答案】6
【解答】解:过点D作DE⊥AB于E,过点C作CF⊥AB于F.
∵CD∥AB,DE⊥AB,CF⊥AB,
∴DE=CF,
在Rt△CFB中,CF=BC•sin45°=3(米),
∴DE=CF=3(米),
在Rt△ADE中,∵∠A=30°,∠AED=90°,
∴AD=2DE=6(米),
故答案为:6.
4.(2020•泰安)如图,某校教学楼后面紧邻着一个山坡,坡上面是一块平地.BC∥AD,BE⊥AD,斜坡AB长26m,斜坡AB的坡比为12:5.为了减缓坡面,防止山体滑坡,学校决定对该斜坡进行改造.经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.如果改造时保持坡脚A不动,则坡顶B沿BC至少向右移 m时,才能确保山体不滑坡.(取tan50°≈1.2)
【答案】10
【解答】解:在BC上取点F,使∠FAE=50°,过点F作FH⊥AD于H,
∵BF∥EH,BE⊥AD,FH⊥AD,
∴四边形BEHF为矩形,
∴BF=EH,BE=FH,
∵斜坡AB的坡比为12:5,
∴=,
设BE=12xm,则AE=5xm,
由勾股定理得,AE2+BE2=AB2,即(5x)2+(12x)2=262,
解得,x=2,
∴AE=10m,BE=24m,
∴FH=BE=24m,
在Rt△FAH中,tan∠FAH=,
∴AH=≈20(m),
∴BF=EH=AH﹣AE=10(m),
∴坡顶B沿BC至少向右移10m时,才能确保山体不滑坡,
故答案为:10.
5.(2021•黔西南州)如图,热气球的探测器显示,从热气球底部A处看一栋楼顶部的俯角为30°,看这栋楼底部的俯角为60°,热气球A处与地面距离为150m,则这栋楼的高度是 m.
【答案】100
【解答】解:如图,过A作AH⊥BC,交CB的延长线于点H,
在Rt△ACD中,
∵∠CAD=30°,AD=150m,
∴CD=AD•tan30°=150×=50(m),
∴AH=CD=50m.
在Rt△ABH中,
∵∠BAH=30°,AH=50m,
∴BH=AH•tan30°=50×=50(m),
∴BC=AD﹣BH=150﹣50=100(m),
答:这栋楼的高度为100m.
故答案为:100.
6.(2021•广西)如图,从楼顶A处看楼下荷塘C处的俯角为45°,看楼下荷塘D处的俯角为60°,已知楼高AB为30米,则荷塘的宽CD为 米(结果保留根号).
【答案】(30﹣10)
【解答】解:由题意可得,∠ADB=60°,∠ACB=45°,AB=30m,
在Rt△ABC中,
∵∠ACB=45°,
∴AB=BC,
在Rt△ABD中,
∵∠ADB=60°,
∴BD=AB=10(m),
∴CD=BC﹣BD=(30﹣10)m,
故答案为:(30﹣10).
7.(2019•潍坊)自开展“全民健身运动”以来,喜欢户外步行健身的人越来越多,为方便群众步行健身,某地政府决定对一段如图1所示的坡路进行改造.如图2所示,改造前的斜坡AB=200米,坡度为1:;将斜坡AB的高度AE降低AC=20米后,斜坡AB改造为斜坡CD,其坡度为1:4.求斜坡CD的长.(结果保留根号)
【答案】米
【解答】解:∵∠AEB=90°,AB=200米,坡度为1:,
∴tan∠ABE=,
∴∠ABE=30°,
∴AE=AB=100米,
∵AC=20米,
∴CE=80米,
∵∠CED=90°,斜坡CD的坡度为1:4,
∴,
即,
解得,ED=320米,
∴CD==米,
答:斜坡CD的长是米.
1.(2021•双阳区一模)某课外数学兴趣小组的同学进行关于测量楼房高度的综合实践活动.如图,他们在距离楼房35米的C处测得楼顶的仰角为α,则楼房AB的高为( )
A.35sinα米 B.35tanα米 C.米 D.米
【答案】B
【解答】解:在Rt△ABC中,∵∠ABC=90°,∠ACB=α,BC=35米,
∴AB=BC•tanα=35tanα(米),
答:楼房AB的高为35tanα米.
故选:B.
2.(2021•南山区校级二模)如图,从一热气球的探测器A点,看一栋高楼顶部的仰角为55°,看这栋高楼底部的俯角为35°,若热气球与高楼的水平距离为35m,则这栋高楼度大约是( )(考数据:sin55°≈,cos55°≈,tan55°≈)
A.74米 B.80米 C.84米 D.98米
【答案】A
【解答】解:过点A作AD⊥BC于D,
在Rt△ABD中,∠BAD=55°,AD=35m,tan∠BAD=,
∴BD=AD•tan∠BAD≈35×=49(m),
在Rt△ACD中,∠ACD=90°﹣∠CAD=55°,AD=35m,tan∠ACD=,
∴CD=≈=25(m),
∴BC=BD+CD=49+25=74(m),
故选:A.
3.(2021•长春模拟)如图,建筑工地划出了三角形安全区△ABC,一人从A点出发,沿北偏东53°方向走50m到达C点,另一人从B点出发,沿北偏西53°方向走100m到达C点,则点A与点B相距( )(tan53°≈)
A. B. C. D.130m
【答案】B
【解答】解:如图,过C作CF⊥AD,CE∥AD,BE∥AG,
∴∠CEB=90°,∠GAC=∠ACF=∠EBC=∠BCF=53°,AC=50,BC=100,四边形CEDF是矩形,
∴DE=CF,DF=CE,
在Rt△ACF中,tan∠ACF==tan53°,
在Rt△BCE中,tan∠EBC==tan53°,
∵tan53°≈,
∴==,
∴AF=CF,CE=BE,
在Rt△ACF中,AF2+CF2=AC2,
∴CF2+(CF)2=502,
解得CF=DE=30,AF=×30=40,
在Rt△BCE中,BE2+CE2=BC2,
∴BE2+(BE)2=1002,
解得BE=60,CE=DF=×60=80,
∴AD=AF+DF=120,BD=BE﹣DE=30,
在Rt△ABD中,AD2+BD2=AB2,
∴AB==30.
故选:B.
4.(2021•松北区三模)如图,胡同左右两侧是竖直的墙,一架3米长的梯子BC斜靠在右侧墙壁上,测得梯子与地面的夹角为45°,此时梯子顶端B恰巧与墙壁顶端重合.因梯子阻碍交通,故将梯子底端向右移动一段距离到达D处,此时测得梯子AD与地面的夹角为60°,则胡同左侧的通道拓宽了( )
A.米 B.3米 C.(3﹣)米 D.(3﹣)米
【答案】D
【解答】解:在Rt△EBC中,∠BCE=45°,
∴EC=EB=BC=×3=3(米),
在Rt△BDE中,tan∠BDE=,
∴DE===(米),
∴CD=EC﹣DE=(3﹣)米,
故选:D.
5.(2021•河南模拟)如图,AD是土坡AB左侧的一个斜坡,坡度为55°,村委会在坡底D处建另一个高为3米的平台,并将斜坡AD改为AC,坡比i=1:1,求土坡AB的高度.(精确到0.1米,参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43.)
【答案】10.0米
【解答】解:过点C作CE⊥AB于E,
设AE=x米,
∵CD⊥BD,AB⊥CD,
∴四边形CDBE为矩形,
∴BE=CD=3米,CE=DB,
∵斜坡AC的坡比i=1:1,
∴CE=AE=x米,
∴AB=(x+3)米,
在Rt△ADB中,tan∠ADB=,即≈1.43,
解得:x≈6.98,
则AB=x+3=9.98≈10.0(米),
答:土坡AB的高度约为10.0米.
6.(2021•九江模拟)如图1是甘棠湖上的一座拱桥,图2是其侧面示意图,斜道AB的坡度tanA=,斜道CD的坡度tanD=,得湖宽AD=76米,AB=10米,CD=12米,已知所在圆的圆心O在AD上.
(1)分别求点B,C到直线AD的距离;
(2)求的长.
【答案】(1)点B到直线AD的距离为10米,点C到直线AD的距离为12米
(2)π
【解答】解:(1)过点B作BE⊥AD于E,过点C作CF⊥AD于F,
在Rt△BAE中,tanA=,即=,
设BE=x米,则AE=3x米,
由勾股定理得:BE2+AE2=AB2,即x2+(3x)2=(10)2,
解得:x1=10,x2=﹣10(舍去),
∴BE=10米,AE=30米,
在Rt△DCF中,tanD=,即=,
设CF=y米,则DF=2y米,
由勾股定理得:CF2+DF2=CD2,即y2+(2y)2=(12)2,
解得:y1=12,22=﹣12(舍去),
∴CF=12米,DF=24米,
答:点B到直线AD的距离为10米,点C到直线AD的距离为12米;
(2)连接OB、OC,
∵AD=76米,AE=30米,DF=24米,
∴EF=76﹣30﹣24=22米,
设OE=z米,则OF=(22﹣z)米,
在Rt△BEO中,OB2=BE2+OE2,
在Rt△CFO中,OC2=CF2+OF2,
∴BE2+OE2=CF2+OF2,即102+z2=122+(22﹣z)2,
解得:z=12,
则OE=12米,OF=10米,
∴△BEO≌△OFC,
∴∠BOE=∠OCF,
∵∠COF+∠OCF=90°,
∴∠COF+∠BOE=90°,
∴∠BOC=90°,
在Rt△BEO中,OB===2(米),
∴的长==π(米).
7.(2021•九龙坡区模拟)重庆市某校数学兴趣小组在水库某段CD的附近借助无人机进行实物测量的社会实践活动.如图所示,兴趣小组在水库正面左岸的C处测得水库右岸D处某标志物DE顶端的仰角为α.在C处一架无人飞机以北偏西90°﹣β方向飞行100米到达点A处,无人机沿水平线AF方向继续飞行30米至B处,测得正前方水库右岸D处的俯角为30°.线段AM的长为无人机距地面的铅直高度,点M、C、D在同一条直线上.
(1)求无人机的飞行高度AM;
(2)求标志物DE的高度.(结果精确到0.1米)
(已知数据:sinα=,cosα=,tanα=,sinβ=,cosβ=,tanβ=2,≈1.732)
【答案】(1) AM为200 (2) 207.3米
【解答】解:(1)根据题意可知:∠ACM=β,AC=100米,
∴AM=AC•sinβ=100×=200(米),
答:无人机的飞行高度AM为200米;
(2)根据题意可知:∠ECD=α,AB=30米,∠FBD=30°,
如图,作BG⊥MC于点G交AC于点H,
∵AB∥CM,
∴∠BAH=∠ACM=β,
∴BH=AB•tanβ=30×2=60(米),
∴HG=BG﹣BH=200﹣60=140(米),
∵AB∥CM,
∴△HBA∽△HGC,
∴AB:GC=BH:HG,
∴30:GC=60:140,
解得GC=70(米),
∵∠GBD=90°﹣30°=60°,
∴GD=BG•tan∠GBD=200×=200(米),
∴CD=GD﹣GC=(200﹣70)米,
∴DE=CD•tanα=(200﹣70)×≈207.3(米).
答:标志物DE的高度为207.3米.
中考数学一轮复习知识点梳理+练习考点24 解直角三角形的实际应用(含解析): 这是一份中考数学一轮复习知识点梳理+练习考点24 解直角三角形的实际应用(含解析),共1页。
(通用版)中考数学一轮复习考点练习24 解直角三角形的实际应用(教师版): 这是一份(通用版)中考数学一轮复习考点练习24 解直角三角形的实际应用(教师版),共1页。
初中数学中考复习 考点24 解直角三角形-中考数学考点一遍过: 这是一份初中数学中考复习 考点24 解直角三角形-中考数学考点一遍过,共23页。试卷主要包含了锐角三角函数的定义,特殊角的三角函数值,解直角三角形,解直角三角形的应用等内容,欢迎下载使用。












