



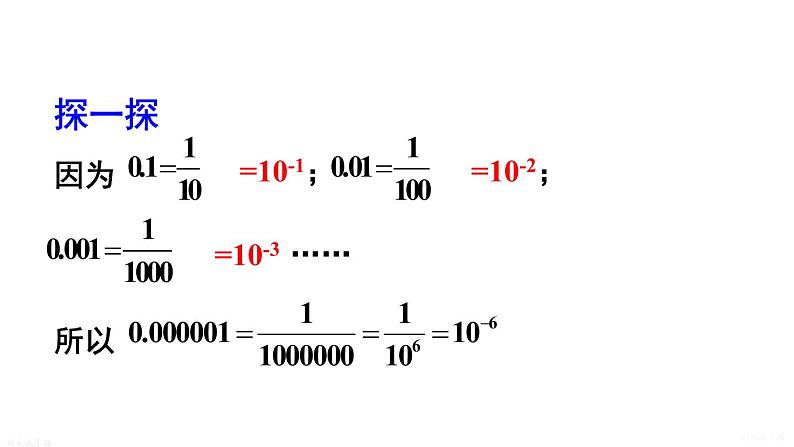



还剩10页未读,
继续阅读
16.4.2 科学记数法 华师版数学八年级下册上课课件
展开
这是一份16.4.2 科学记数法 华师版数学八年级下册上课课件,共18页。
2.科学记数法华师大版 八年级数学下册16.4 零指数幂与负整数指数幂状元成才路状元成才路用科学记数法表示下列各数:1.地球半径约为686000000米.2.光的速度约为300000000m/s.3.地球离太阳约为一万五千万米.4.地球上煤的储量估计在15万亿吨以上.试一试状元成才路状元成才路状元成才路状元成才路思考:下面的数该如何表示? 1.细胞的直径只有一微米,即0.000001米.2.一种计算机完成一次基本操作运算的时间约为1纳秒,即0.000000001秒.3.一个氧原子的质量为0.000 000 000 000 000 000 000 000 02657kg. 上面这些较小的数能否用科学记数法来表示呢?该如何表示?状元成才路状元成才路状元成才路状元成才路科学记数法:绝对值大于10的数记成a×10n的形式,其中1≤a<10,n是正整数.例:2280000可以写成 ___________ .想一想怎样把0.000001用科学记数法表示?2.28×106状元成才路状元成才路状元成才路状元成才路探一探因为=10-1;=10-2;=10-3 ……所以状元成才路状元成才路状元成才路状元成才路 类似地,我们可以利用10的负整数次幂,用科学记数法表示一些绝对值较小的数,即将它们表示成 a×10-n 的形式,其中 n 是正整数,1≤|a|<10.状元成才路状元成才路状元成才路状元成才路试一试把﹣0.00043 用科学记数法表示.状元成才路状元成才路状元成才路状元成才路 可见,绝对值小于1的数可记成±a×10-n的形式,其中1≤a<10,n是正整数,n等于原数中第一个不等于零的数字前面的零的个数(包括小数点前面的一个零),这种记数方法也是科学记数法.状元成才路状元成才路状元成才路状元成才路例 用科学记数法表示下列各数:(1)0.000 76; (2)﹣0.000 001 59.解:(1)0.000 76 = 7.6×0.000 1 = 7.6×10-4.(2)-0.000 001 59 = -1.59×0.000 001 = -1.59×10-6.状元成才路状元成才路状元成才路状元成才路练一练1.用科学记数法表示下列各数:(1) 0.000 0032= (2) -0.000 00014=(3) -680 000 000=(4) 314 000 000 000=3.2×10-6-1.4×10-76.8×1083.14×1011状元成才路状元成才路状元成才路状元成才路2. 随着微电子制造技术的不断进步,半导体材料的精加工尺寸大幅度缩小,目前已经能够在350平方毫米的芯片上集成5亿个元件,问1个这样的元件大约占多少平方毫米?解:350÷(5×108)=350÷5×10-8=70×10-8=7×10-7(平方毫米).所以1个这样的元件大约占7×10-7平方毫米.状元成才路状元成才路状元成才路状元成才路1. 数据 0.0000314 用科学记数法表示为( )A. 31.4×10-4 B. 3.14×10-5C. 3.14×10-6 D. 0.314×10-6B状元成才路状元成才路状元成才路状元成才路2. 已知空气的单位体积质量为 1.24×10-3 克/厘米3,1.24×10-3 用小数表示为( )A. 0.000124 B. 0.0124C. -0.00124 D. 0.00124D状元成才路状元成才路状元成才路状元成才路3. 用科学记数法表示下列各数:(1)0.000 3; (2)-0.000 006 4;(3)0.000 031 4; (4)2013 0003×10-4-6.4×10-63.14×10-52.013×106状元成才路状元成才路状元成才路状元成才路4.计算:状元成才路状元成才路5. 一根头发丝的直径为6万nm(纳米),某种生物细胞的直径为1μm(微米).请你选择适当的方法说明两者之间的差距(1nm=10-9m,1μm=10-6m).解:因为6万nm=6×104×10-9m=6×10-5m,所以6×10-5÷(1×10-6)=6×10-5+6=60,即一根头发丝的直径是该种生物细胞直径的60倍.状元成才路状元成才路状元成才路状元成才路课后小结 我们可以利用10的负整数次幂,用科学记数法表示一些绝对值较小的数,即将它们表示成 a×10-n 的形式,其中 n 是正整数,1≤|a|<10.状元成才路状元成才路1.从教材习题中选取.2.完成练习册本课时的习题.课后作业状元成才路状元成才路
2.科学记数法华师大版 八年级数学下册16.4 零指数幂与负整数指数幂状元成才路状元成才路用科学记数法表示下列各数:1.地球半径约为686000000米.2.光的速度约为300000000m/s.3.地球离太阳约为一万五千万米.4.地球上煤的储量估计在15万亿吨以上.试一试状元成才路状元成才路状元成才路状元成才路思考:下面的数该如何表示? 1.细胞的直径只有一微米,即0.000001米.2.一种计算机完成一次基本操作运算的时间约为1纳秒,即0.000000001秒.3.一个氧原子的质量为0.000 000 000 000 000 000 000 000 02657kg. 上面这些较小的数能否用科学记数法来表示呢?该如何表示?状元成才路状元成才路状元成才路状元成才路科学记数法:绝对值大于10的数记成a×10n的形式,其中1≤a<10,n是正整数.例:2280000可以写成 ___________ .想一想怎样把0.000001用科学记数法表示?2.28×106状元成才路状元成才路状元成才路状元成才路探一探因为=10-1;=10-2;=10-3 ……所以状元成才路状元成才路状元成才路状元成才路 类似地,我们可以利用10的负整数次幂,用科学记数法表示一些绝对值较小的数,即将它们表示成 a×10-n 的形式,其中 n 是正整数,1≤|a|<10.状元成才路状元成才路状元成才路状元成才路试一试把﹣0.00043 用科学记数法表示.状元成才路状元成才路状元成才路状元成才路 可见,绝对值小于1的数可记成±a×10-n的形式,其中1≤a<10,n是正整数,n等于原数中第一个不等于零的数字前面的零的个数(包括小数点前面的一个零),这种记数方法也是科学记数法.状元成才路状元成才路状元成才路状元成才路例 用科学记数法表示下列各数:(1)0.000 76; (2)﹣0.000 001 59.解:(1)0.000 76 = 7.6×0.000 1 = 7.6×10-4.(2)-0.000 001 59 = -1.59×0.000 001 = -1.59×10-6.状元成才路状元成才路状元成才路状元成才路练一练1.用科学记数法表示下列各数:(1) 0.000 0032= (2) -0.000 00014=(3) -680 000 000=(4) 314 000 000 000=3.2×10-6-1.4×10-76.8×1083.14×1011状元成才路状元成才路状元成才路状元成才路2. 随着微电子制造技术的不断进步,半导体材料的精加工尺寸大幅度缩小,目前已经能够在350平方毫米的芯片上集成5亿个元件,问1个这样的元件大约占多少平方毫米?解:350÷(5×108)=350÷5×10-8=70×10-8=7×10-7(平方毫米).所以1个这样的元件大约占7×10-7平方毫米.状元成才路状元成才路状元成才路状元成才路1. 数据 0.0000314 用科学记数法表示为( )A. 31.4×10-4 B. 3.14×10-5C. 3.14×10-6 D. 0.314×10-6B状元成才路状元成才路状元成才路状元成才路2. 已知空气的单位体积质量为 1.24×10-3 克/厘米3,1.24×10-3 用小数表示为( )A. 0.000124 B. 0.0124C. -0.00124 D. 0.00124D状元成才路状元成才路状元成才路状元成才路3. 用科学记数法表示下列各数:(1)0.000 3; (2)-0.000 006 4;(3)0.000 031 4; (4)2013 0003×10-4-6.4×10-63.14×10-52.013×106状元成才路状元成才路状元成才路状元成才路4.计算:状元成才路状元成才路5. 一根头发丝的直径为6万nm(纳米),某种生物细胞的直径为1μm(微米).请你选择适当的方法说明两者之间的差距(1nm=10-9m,1μm=10-6m).解:因为6万nm=6×104×10-9m=6×10-5m,所以6×10-5÷(1×10-6)=6×10-5+6=60,即一根头发丝的直径是该种生物细胞直径的60倍.状元成才路状元成才路状元成才路状元成才路课后小结 我们可以利用10的负整数次幂,用科学记数法表示一些绝对值较小的数,即将它们表示成 a×10-n 的形式,其中 n 是正整数,1≤|a|<10.状元成才路状元成才路1.从教材习题中选取.2.完成练习册本课时的习题.课后作业状元成才路状元成才路
相关资料
更多









