2023届上海市洋泾中学高三上学期10月月考数学试题（解析版）

2023届上海市洋泾中学高三上学期10月月考数学试题

一、单选题

1．设x，，则是的（    ）

A．充分不必要条件 B．必要不充分条件

C．充要条件 D．既不充分也不必要条件

【答案】B

【分析】分别作出与的区域，即可判断.

【详解】分别作出与的图象如图，

表示圆及内部，表示正方形及内部，显然 ，，则是的必要不充分条件.

故选B．

【点睛】本题主要考查充要条件的判断，利用“小范围大范围，大范围小范围”，考查逻辑推理与数形结合思想，属于基础题.

2．关于三个不同平面与直线，下列命题中的假命题是（       ）

A．若，则内一定存在直线平行于

B．若与不垂直，则内一定不存在直线垂直于

C．若，，，则

D．若，则内所有直线垂直于

【答案】D

【分析】对四个选项，利用正方体中的线和面的关系，逐一验证，由此得出是假命题的选项.

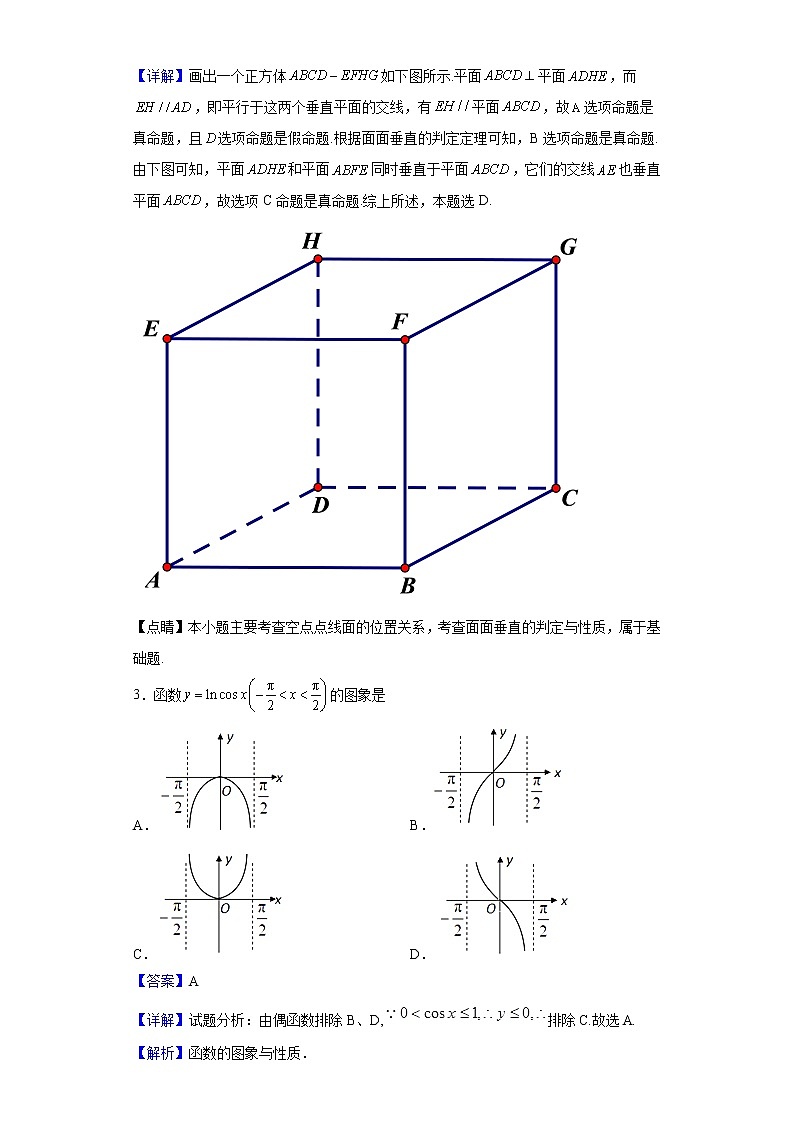
【详解】画出一个正方体如下图所示.平面平面，而，即平行于这两个垂直平面的交线，有平面，故选项命题是真命题，且选项命题是假命题.根据面面垂直的判定定理可知，B选项命题是真命题.由下图可知，平面和平面同时垂直于平面，它们的交线也垂直平面，故选项C命题是真命题.综上所述，本题选D.

【点睛】本小题主要考查空点点线面的位置关系，考查面面垂直的判定与性质，属于基础题.

3．函数的图象是

A． B．

C． D．

【答案】A

【详解】试题分析：由偶函数排除B、D,排除C.故选A.

【解析】函数的图象与性质．

4．设、、是定义域为的三个函数，对于命题：①若、、均为增函数，则、、中至少有一个增函数；②若、、均是以为周期的函数，则、、均是以为周期的函数，下列判断正确的是

A．①和②均为真命题

B．①和②均为假命题

C．①为真命题，②为假命题

D．①为假命题，②为真命题

【答案】D

【详解】试题分析：

因为，所以,又、、均是以为周期的函数，所以，所以是周期为的函数，同理可得、均是以为周期的函数，②正确；增函数加减函数也可能为增函数，因此①不正确.选D.

【解析】抽象函数、函数的单调性、函数的周期性

【名师点睛】本题主要考查抽象函数的单调性与周期性，是高考常考内容.本题有一定难度.解答此类问题时，关键在于灵活选择方法，如结合选项或通过举反例应用“排除法”等.本题能较好地考查考生分析问题与解决问题的能力、基本计算能力等.

二、填空题

5．设全集，，，则___________.

【答案】

【分析】根据补集贺交集的定义即可得解.

【详解】解：因为，

所以或，

所以.

故答案为：.

6．若复数满足，其中为虚数单位，则_________．

【答案】

【详解】设，则

【解析】复数相等，共轭复数

7．如果展开式中各项系数的和等于，则展开式中第项是__________.

【答案】

【分析】利用各项系数和可得出的值，然后利用二项展开式通项可求得结果.

【详解】因为展开式中各项系数的和为，解得，

所以，展开式中第三项为.

故答案为：.

8．抛物线（）上的动点到焦点的距离的最小值为，则_______．

【答案】

【详解】因为抛物线上动点到焦点的距离为动点到准线的距离，因此抛物线上动点到焦点的最短距离为顶点到准线的距离，即

9．已知α∈.若幂函数f(x)＝xα为奇函数，且在(0，＋∞)上递减，则＝______.

【答案】-1

【分析】根据幂函数，当为奇数时，函数为奇函数，时，函数在(0，＋∞)上递减，即可得出答案.

【详解】解：∵幂函数f(x)＝xα为奇函数，∴可取－1，1，3，

又f(x)＝xα在(0，＋∞)上递减，∴α＜0，故＝－1.

故答案为：-1.

10．已知定义在上的函数周期为，且当，，则_________.

【答案】1

【分析】利用函数的周期性，直接代入求值即可.

【详解】定义在上的函数周期为，且，，

故答案为：1

11．已知正实数，满足，则的最大值为_________.

【答案】

【解析】利用基本不等式可求得的范围，等式两边同时平方即可得解.

【详解】，，当且仅当即时等号成立，

，即的最大值为.

故答案为：

12．在一个盒子中有大小质地相同的10个球，其中6个红球，4个白球，两个人依次不放回地摸一个球，在第一个人摸出1个红球的条件下，第2个人摸出1个白球的概率是_________.

【答案】

【分析】根据概率的定义计算．

【详解】在第一个人摸出1个红球的条件下，盒子中还有5个红球，4个白球，第2个人摸出1个白球的概率为．

故答案为：．

13．方程在区间上的解为___________．

【答案】

【详解】试题分析：

化简得：，所以，解得或（舍去），又，所以.

【解析】二倍角公式及三角函数求值

【名师点睛】已知三角函数值求角，基本思路是通过化简 ，得到角的某种三角函数值，结合角的范围求解. 本题难度不大，能较好地考查考生的逻辑推理能力、基本计算能力等.

14．设函数若不等式的解集为则实数的取值范围为___________.

【答案】

【分析】利用分段函数，结合指数函数的单调性，推出不等式，求解即可得到答案．

【详解】，且，设函数，若不等式的解集是，，

当时，，可得，解得；

当，即时，，不等式恒成立可得．

综上可得．

实数的取值范围为：，．

故答案为：，．

【点睛】本题考查分段函数的应用，函数的单调性的应用，考查分析问题解决问题的能力，是中档题．

15．定义域为的函数图象的两个端点为、，是图象上任意一点，过点作垂直于轴的直线交线段于点 (点与点可以重合)，我们称的最大值为该函数的“曲径”. 则定义域为上的函数的曲径是___________.

【答案】

【分析】由题意得端点，可求出直线的方程，然后令，利用导数求出函数在上的最值，从而可求得答案.

【详解】由题意得端点，则，

所以直线的方程为，

令（），

则，

当时，，当时，，

所以在上递增，在上递减，

所以当时，取得最大值，即，

因为，，

所以，

所以，所以，

所以的最大值为，

即定义域为上的函数的曲径是，

故答案为：.

16．如图，已知是半径为圆心角为的一段圆弧上的一点，若，则的取值范围是__________．

【答案】

【分析】建立如图平面直角坐标系，运用坐标法可得，即可讨论值域

【详解】如图所示，建立平面直角坐标系，则，，， ，

由，则，即有，

∵，∴.

故答案为：

三、解答题

17．如图，直三棱柱内接于高为的圆柱中，已知，，，为的中点.

(1)求圆柱的表面积；

(2)求二面角的大小.

【答案】(1)

(2)

【分析】（1）由勾股定理可求得底面圆的半径，分别求得圆柱的侧面积和底面积，进而可求得表面积；

（2）方法一：连接，可证得，则可得所求二面角的平面角为，根据长度关系可得结果；

方法二：以为坐标原点可建立空间直角坐标系，利用二面角的向量求法可求得结果.

【详解】(1)，，，

底面圆的半径，圆柱的侧面积为，

又圆柱的底面积为，圆柱的表面积.

(2)方法一：连接，

平面，平面，；

，即，，平面，

平面，又平面，；

即为二面角的平面角，

，，，，

即二面角的大小为.

方法二：以为坐标原点，正方向为轴，可建立如图所示空间直角坐标系，

则，，，，，

设平面的法向量，

则，令，解得：，，；

轴平面，是平面的一个法向量，

，

由图形可知：二面角为锐二面角，

二面角的大小为，即.

18．已知,,为△ABC的三个内角，向量，，且．

（1）求的大小；

（2）若，求△ABC的面积．

【答案】(1)；(2)．

【分析】(1)由题意结合向量垂直的充分必要条件得到三角方程，结合三角形的特征和三角方程可得∠A的大小；

(2)由题意结合余弦定理得到的值，然后结合面积公式即可求得△ABC的面积.

【详解】（1）由，可得·=0，

即·，又，，

所以，

即，又，

∴，故．

（2）在△ABC中，由，

可得，

即，

故，

∴．

【点睛】在处理三角形中的边角关系时，一般全部化为角的关系，或全部化为边的关系．题中若出现边的一次式一般采用到正弦定理，出现边的二次式一般采用到余弦定理．应用正、余弦定理时，注意公式变式的应用．解决三角形问题时，注意角的限制范围．

19．已知函数，其中.

(1)求的单调区间；

(2)当时，记在区间的最大值为，最小值为，求的取值范围.

【答案】(1)单调递增区间为、，减区间为

(2)

【分析】（1）利用导数与函数单调性的关系可求得函数的增区间和减区间；

（2）分、两种情况讨论，结合（1）中的结论求出、的表达式，结合导数法与函数的单调性可求得的取值范围.

【详解】(1)解：函数的定义域为，，

当时，由可得，由可得或，

所以，函数的单调递增区间为、，减区间为.

(2)解：因为，则，则函数在区间上单调递减，在上单调递增，

所以，当时，，

因为，，则，

所以，，令.

①若，则，

，故函数在上单调递减，此时；

②若，则.

综上所述，的取值范围是.

【点睛】方法点睛：求函数在区间上的最值的方法：

（1）若函数在区间上单调，则与一个为最大值，另一个为最小值；

（2）若函数在区间内有极值，则要求先求出函数在区间上的极值，再与、比大小，最大的为最大值，最小的为最小值；

（3）若函数在区间上只有唯一的极大点，则这个极值点就是最大（最小）值点，此结论在导数的实际应用中经常用到.

20．已知、分别是椭圆的左右顶点，为坐标原点，，点在椭圆上．过点，且与坐标轴不垂直的直线交椭圆于、两个不同的点．

(1)求椭圆的标准方程；

(2)若点落在以线段为直径的圆的外部，求直线的斜率的取值范围；

(3)当直线的倾斜角为锐角时，设直线、分别交轴于点、，记，，求的取值范围．

【答案】(1)

(2)

(3)

【分析】（1）根据长轴长求出，再代入，求出，得到椭圆方程；

（2）设出直线的方程，联立椭圆方程，先根据根的判别式求出的取值范围，

再根据点落在以线段为直径的圆的外部，则，列出不等式，求出的取值范围；

（3）先设出直线的方程，求出点S坐标，同理求出点T为，根据向量关系得到，结合的范围求出的范围.

【详解】(1)因为，所以；

又点在图像上即，所以，

所以椭圆的方程为；

(2)由（1）可得

设直线，设、，

由得，

解得或①

∵点在以线段为直径的圆的外部，则，

又②

解得或    

由①②得

(3)设直线，又直线的倾斜角为锐角，由（2）可知，

记、，所以直线的方程是：，直线的方程是：.

令，解得，所以点S坐标为；同理点T为.

所以，，.

由，，可得：，，

所以，

由（2）得，，

所以

，

因为，所以，，

故的范围是.

【点睛】对于直线与圆锥曲线结合，求解取值范围问题，通常思路为设出直线方程，与圆锥曲线联立，得到两根之和，两根之积，再根据题干条件列出方程，求出答案.

21．对于数列，定义为数列的差分数列，其中．如果对任意的，都有，则称数列为差分增数列．

（1）已知数列为差分增数列，求实数的取值范围；

（2）已知数列为差分增数列，且，．若，求非零自然数k的最大值；

（3）已知项数为2k的数列（）是差分增数列，且所有项的和等于k，证明：．

【答案】（1）；（2）65；（3）证明见解析．

【分析】（1）利用差分增数列的定义可得关于的不等式组，即可求解；

（2）根据△△，，，可得△△，△，△，，△，，从而可得，即可求解；

（3）利用反证法推出矛盾，即可得证．

【详解】（1）数列1，2，4，，16，24的差分数列为1，2，，，8，

由题意可得，解得，

故实数的取值范围是．

（2）由题意，△，△，

因为数列为差分增数列，所以对任意的，都有△△，

所以△△，△，同理，△，，△，，

所以当时，△△△，

所以，

解得，

所以非零自然数的最大值为65．

（3）证明：假设，

由题意知，2，3，，，

因为项数为的数列所有项的和等于，

所以，

即，

所以，

因为数列，2，3，，是差分增数列，

所以，

所以，因此，

所以对任意的，，都有，即，

所以，

所以与矛盾，

故假设不成立，所以．

【点睛】关键点睛：对于数列的新定义的题，解题的关键是理解清楚题意，熟练掌握数列中常见的解题方法.