2022-2023学年江苏省扬州市宝应中学高一上学期期中数学试题（解析版）

2022-2023学年江苏省扬州市宝应中学高一上学期期中数学试题

一、单选题

1．已知集合，则

A． B． C． D．

【答案】C

【分析】先求，再求．

【详解】由已知得，所以，故选C．

【点睛】本题主要考查交集、补集的运算．渗透了直观想象素养．使用补集思想得出答案．

2．命题：“，”，若命题是真命题，则的取值范围为（    ）

A． B． C． D．

【答案】B

【分析】由题可得，，进而即得.

【详解】由题可知，，

所以，，又，

所以.

故选：B.

3．设，则的最大值为（    ）

A．3 B． C． D．

【答案】C

【分析】利用基本不等式求出函数得最大值.

【详解】因为，所以，当且仅当，即时取等号，

所以，即的最大值为.

故选：C.

4．函数的定义域为(    )

A． B． C． D．

【答案】D

【分析】根据表达式有意义列出不等式组求解即可

【详解】由题知,解得且

即函数的定义域为

故选：D

5．某人去上班，先快速走，后中速走．如果表示该人离单位的距离，表示出发后的时间，那么下列图象中符合此人走法的是（    ）

A． B．

C． D．

【答案】D

【分析】根据已知条件及排除法即可求解.

【详解】当时，距离单位最远，不可能是，排除A，C，先快速走，后中速，则随的变化慢，排除B，

故选：D．

6．已知函数若在单调递减，则实数m的取值范围是（    ）

A． B． C． D．

【答案】D

【分析】利用分段函数的单调性求参数m的取值范围.

【详解】由在单调递减，可得，解得.

故选:D.

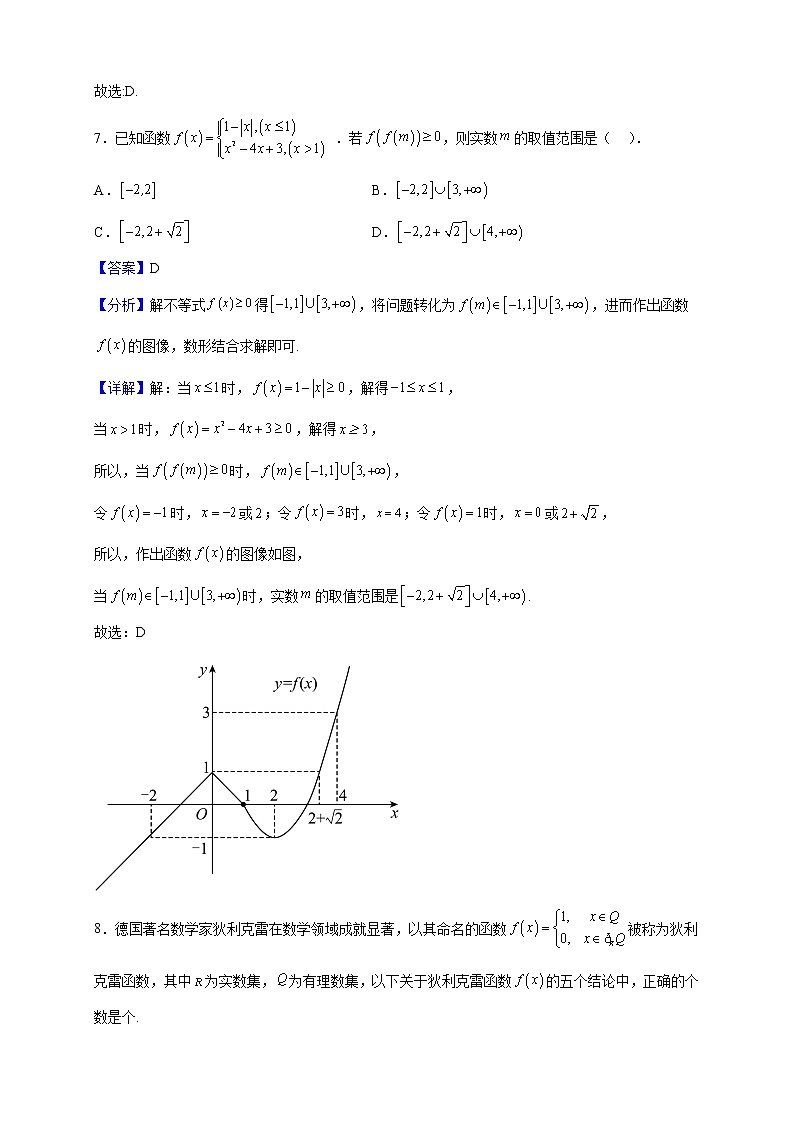
7．已知函数 ．若，则实数的取值范围是（    ）．

A． B．

C． D．

【答案】D

【分析】解不等式得，将问题转化为，进而作出函数的图像，数形结合求解即可.

【详解】解：当时，，解得，

当时，，解得，

所以，当时，，

令时，或；令时，；令时，或，

所以，作出函数的图像如图，

当时，实数的取值范围是.

故选：D

8．德国著名数学家狄利克雷在数学领域成就显著，以其命名的函数被称为狄利克雷函数，其中为实数集，为有理数集，以下关于狄利克雷函数的五个结论中，正确的个数是个.

①函数偶函数；

②函数的值域是；

③若且为有理数，则对任意的恒成立；

④在图象上存在不同的三个点，，，使得为等边角形.

A．1 B．2 C．3 D．4

【答案】D

【分析】当时，，当时，，函数为偶函数，①正确，函数的值域是，②正确，为有理数，则当时，，当时，，故，③正确，，，构成等边三角形，故④正确，得到答案.

【详解】当时，，当时，，故，函数为偶函数，①正确；

函数的值域是，②正确；

为有理数，则当时，，当时，，故，③正确；

，，，故，，构成等边三角形，故④正确；

故选：D.

【点睛】本题考查了函数的新定义问题，意在考查学生的理解能力和对于函数性质的灵活运用.

二、多选题

9．下列命题正确的是（    ）

A．“”是“”的充分不必要条件

B．“三角形为等腰三角形”是“三角形为正三角形”的必要不充分条件

C．若集合是的真子集，则“”是“”的必要不充分条件

D．“关于x的不等式在上恒成立”的充要条件是“”

【答案】BC

【分析】A选项，根据，但得到A错误；

B选项，等边三角形是特殊的等腰三角形，从而得到“三角形为等腰三角形”是“三角形为正三角形”的必要不充分条件；

C选项，由是的真子集得到，但，从而C正确；

D选项，关于x的不等式在上恒成立，分为，两种情况进行求解.

【详解】因为，但，故“”是“”的必要不充分条件，A错误；

三角形是等腰三角形不一定是等边三角形，等边三角形是特殊的等腰三角形，

故“三角形为等腰三角形”是“三角形为正三角形”的必要不充分条件，B正确；

若集合是的真子集，则，但，

所以“”是“”的必要不充分条件，C正确；

关于x的不等式在上恒成立，当，时，满足要求，

若，则需要满足，故D错误.

故选：BC

10．已知关于的不等式的解集是，则下列结论正确的是（    ）

A． B．

C． D．

【答案】ABD

【分析】根据一元二次不等式与相应的一元二次方程的关系，利用根与系数的关系即可判断出结论．

【详解】关于的不等式的解集是，

所以，且是一元二次方程即的两根，

所以，选项A正确；

，选项B正确；

，选项D正确；

由，可得：是错误的，即选项C错误．

故选：ABD．

11．已知函数，则（    ）

A．

B．若，则或

C．的解集为

D．，，则

【答案】BCD

【分析】对于A，根据解析式先求，再求，对于B，分和两种情况求解，对于C，分和两种情况解不等式，对于D，求出函数的最大值判断.

【详解】对于A，因为，所以，所以A错误，

对于B，当时，由，得，得，当时，则，得，，得或（舍去），综上或，所以B正确，

对于C，当时，由，得，解得，当时，由，得，解得，综上，的解集为，所以C正确，

对于D，当时，，当时，，所以的值域为，

因为，，所以，所以D正确，

故选：BCD

12．已知，若对任意的，不等式恒成立，则（    ）

A． B．

C．的最小值为12 D．的最小值为

【答案】ACD

【分析】由已知可得，由于，所以可得当时，，当时，，从而可得，，则，然后代入各选项的式子中结合基本不等式和函数的性质分析判断.

【详解】由，得，

所以，

因为，

所以当时，，当时，，

因为对任意的，不等式恒成立，

所以当时，，当时，，

所以对于函数，有，，所以，

所以A正确，B错误，

对于C，因为，所以，

所以，当且仅当，即时取等号，所以的最小值为12，所以C正确，

对于D，，

令，因为，当且仅当即时取等号，所以，

由，得，所以，

所以，

所以函数在上递增，

所以当时，取得最小值为，

所以的最小值为，所以D正确，

故选：ACD

【点睛】关键点点睛：此题考查不等式恒成立问题，考查基本不等式的应用，解题的关键是由题意结合一次函数和二次函数的性质得，，从而可结合基本不等式分析判断，考查数学转化思想，属于较难题.

三、填空题

13．已知，，全集，则_________.（用区间表示）

【答案】##

【分析】先求解二次不等式和绝对值不等式化简集合，再利用集合的交集和补集运算计算即可.

【详解】由题意，，

，故，

则.

故答案为：

14．已知，若幂函数在区间上单调递增，且其图像不过坐标原点，则______.

【答案】-2.

【分析】根据幂函数的单调性与定义域判定即可.

【详解】因为幂函数图像不过坐标原点，故，又在区间上单调递增，故.

故答案为：.

15．计算：______．

【答案】

【分析】根据换底公式、对数的运算性质计算可得.

【详解】解：

．

故答案为：．

16．设函数，存在最小值时，实数a的取值范围是______；

【答案】

【分析】求出的对称轴为，得到要想存在最小值，需要，单调递减，且在处，的函数值要大于等于的函数值，列出不等式组，求出实数a的取值范围.

【详解】当时，的对称轴为，

要想存在最小值，当时，单调递减，且在处，的函数值要大于等于的函数值，

故且②，解②得：或，

综上：

故答案为：.

四、解答题

17．已知全集.

(1)求；

(2)若集合且，求实数的取值范围.

【答案】(1)

(2)

【分析】先求出集合A、B，分类讨论求出集合C，结合集合的基本运算，从而求得a的取值范围．

【详解】（1）解不等式可得，或，

所以

（2）因为，

当时，，

因为，所以，解得．

当时，，不成立．

当时，，显然不满足题意．

综上知实数的取值范围是．

18．已知集合，．

(1)若“”是“”的充分条件，求实数m的取值范围；

(2)若“”是“”的必要条件，求实数m的取值范围．

【答案】(1)

(2)

【分析】（1）根据题意分析出，再利用数轴得到不等式组，解出范围即可；

（2）分析出，分和进行分类讨论即可.

【详解】（1）

由题可知，所以，解得，

所以实数m的取值范围为.

（2）由题可知，

当时，，即，此时满足题意；

当时，，解得，

综上所述，实数m的取值范围为．

19．已知幂函数在上是减函数.

(1)求的解析式；

(2)若，求的取值范围.

【答案】(1)

(2)（2，5）.

【分析】（1）根据幂函数的性质可求得的值.

（2）根据幂函数的单调性解不等式求参数.

【详解】（1）解：由题意得：

根据幂函数的性质可知，即，解得或.

因为在上是减函数，所以，即，则.

故.

（2）由（1）可得，设，

则的定义域为，且在定义域上为减函数.

因为，所以

解得.

故的取值范围为（2，5）.

20．已知函数是奇函数，是偶函数.

(1)求.

(2)判断函数在上的单调性并说明理由，再求函数在上的最值.

(3)若函数满足不等式，求出t的范围.

【答案】(1)

(2)是区间上的增函数，理由见解析，

(3)

【分析】（1）由函数的奇偶性定义以及性质求解即可；

（2）利用定义证明单调性，进而得出最值；

（3）由在区间上的单调性以及奇偶性，解不等式得出t的范围.

【详解】（1）因为在是奇函数

验证：，，函数为奇函数；

为偶函数，则

验证：，，函数为偶函数.

（2）是区间上的增函数，理由如下：

设是区间上任意两个实数，且，

则

因为所以

是区间上的增函数

（3）因为是区间上的增函数，且是奇函数，

由满足

，即t的范围是

21．已知，函数

(1)当时，画出函数的图像，并结合图像写出函数的单调递增区间；

(2)当时，求在区间上的最大值；

(3)设，函数在区间上既有最大值又有最小值，请直接写出p，q的取值范围（用a表示），不必书写过程．

【答案】(1)图象见解析，递增区间是；

(2)答案见解析；

(3)答案见解析.

【分析】（1）把代入，将函数分段表示出，画出函数图象，求出单调增区间作答.

（2）由（1）的函数解析式，分段求出函数最大值作答.

（3）按与分别画出函数图象，借助图象求出p，q范围作答.

【详解】（1）当时，，其图象如图：

观察图象得：函数的单调递增区间是.

（2）由（1）知，当时，函数在上单调递增，，

当时，，当时，因在上单调递增，

当，即时，，当时，，

所以当时，；当时，；当时，

（3）函数，因函数在开区间上既有最大值又有最小值，

则函数的最值点只能是开区间的内点，则有，

当时，如图1，，解得，，

当时，如图2，，解得，，

所以当时，实数p，q的取值范围分别是，；

当时，实数p，q的取值范围分别是，.

22．若函数满足：存在整数，使得关于的不等式的解集恰为（），则称函数为函数.

(1)若函数为函数，请直接写出（不要过程）；

(2)判断函数是否为函数，并说明理由；

(3)是否存在实数使得函数为函数，若存在，请求出的值；若不存在，请说明理由.

【答案】(1)

(2)不是，理由见解析

(3)存在，

【分析】（1）结合函数的定义列方程、不等式，由此求得的值.

（2）结合函数的定义以及反证法进行判断.

（3）结合函数的定义列方程、不等式，由此求得的值，从而确定正确答案.

【详解】（1）函数为二次函数，对称轴为，开口向上，

若函数为函数，

所以，即，

解得.

（2）函数不是P函数，理由如下：

在上递增，

因为m，n为整数，由题意可知，即，

令，即，解得，

假设函数为P函数，

则，即，与已知矛盾，所以不存在这样的m，n，

所以函数不是P函数；

（3）函数为二次函数，对称轴为，开口向上，

因为关于x的不等式的解集恰为

所以，即

将①代入③得，，

又m，n为整数，，所以，解得，此时，满足题意，

综上所述，存在实数使得函数为P函数.

【点睛】对于函数新定义的题目，解题的关键点在于将“新定义”的问题转化为所学过的知识进行求解.本题中，第（1）（3）两问是二次函数，函数图象有对称性；第（2）问是单调函数.这两种情况列式不一样，但也是围绕 “新定义”去列式.