2022-2023学年湖北省潜江市园林高级中学高二上学期期中数学试题（解析版）

2022-2023学年湖北省潜江市园林高级中学高二上学期期中数学试题

一、单选题

1．已知为平面的一个法向量，为内的一点，则点到平面的距离为（    ）

A． B． C． D．

【答案】A

【分析】根据给定条件，利用点到平面的向量求法，列式计算作答.

【详解】依题意，，而为平面的一个法向量，

所以点到平面的距离.

故选：A

2．已知椭圆的上焦点为，以点为圆心，且与一条坐标轴相切的圆的方程为（    ）

A． B．

C． D．

【答案】A

【解析】先求出点，由题意知圆的半径为即可得圆的方程.

【详解】由题意，椭圆的上焦点为在轴正半轴上，

故所求圆只能是与轴相切，切点为原点，

所以，

可得圆的方程为：，即.

故选：A

3．已知空间向量，，满足，，，，则与的夹角为（    ）

A． B． C． D．

【答案】C

【分析】将，两边平方，利用空间向量的数量积即可得选项.

【详解】设与的夹角为．由，得，两边平方，得，

所以，解得，又，所以，

故选：C．

4．若抛物线的弦AB中点坐标为，则直线AB的斜率为（    ）

A．－4 B．4 C．－2 D．2

【答案】B

【分析】根据点差法求解即可.

【详解】设，，则.

所以，

所以.

故选：B

5．已知直三棱柱中，，，，则异面直线与所成角的余弦值为（    ）

A． B． C． D．

【答案】C

【分析】由题知，，进而利用向量求解异面直线所成角即可.

【详解】解：由题知，在直三棱柱中，平面，平面，

∵平面，平面，

∴，，

∵，，

∴.

∵，，

∴，

∴异面直线与所成角的余弦值为

故选：C.

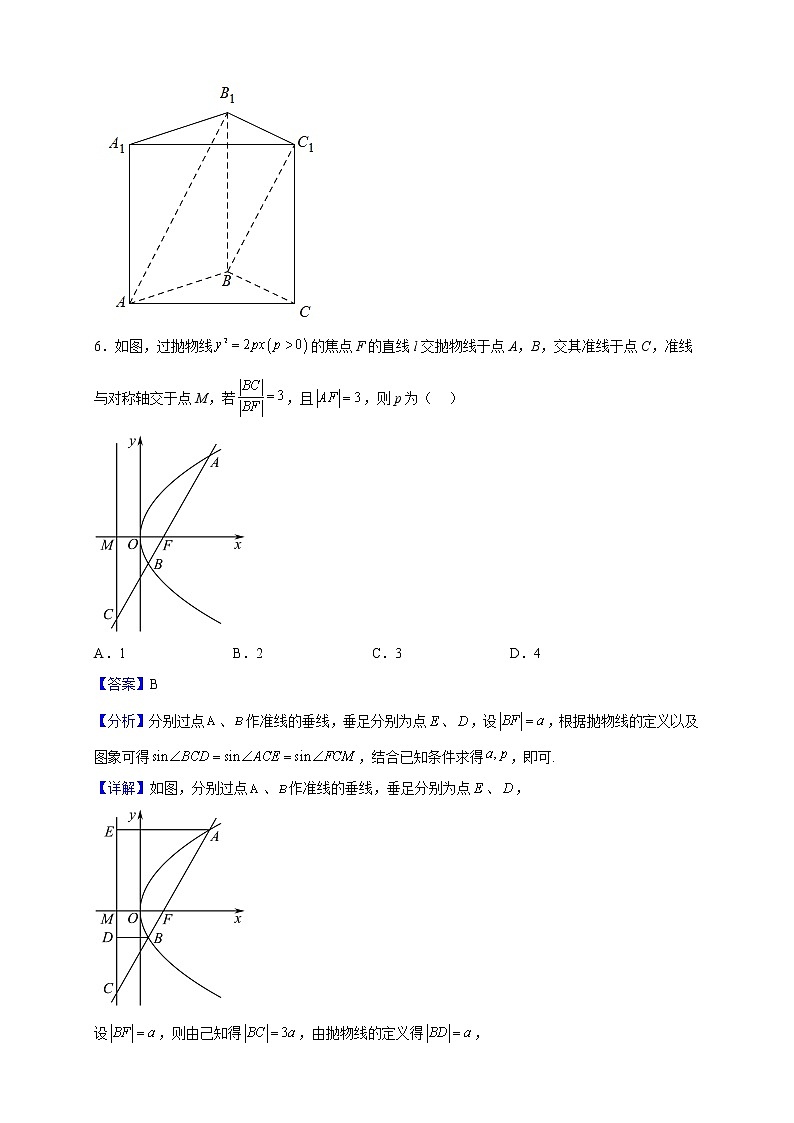
6．如图，过抛物线的焦点F的直线l交抛物线于点A，B，交其准线于点C，准线与对称轴交于点M，若，且，则p为（    ）

A．1 B．2 C．3 D．4

【答案】B

【分析】分别过点、作准线的垂线，垂足分别为点、，设，根据抛物线的定义以及图象可得，结合已知条件求得，即可.

【详解】如图，分别过点、作准线的垂线，垂足分别为点、，

设，则由己知得，由抛物线的定义得，

故，

在直角三角形中，，，

又因为，

则，从而得，

又因为，

所以.

故选：B.

7．已知点、，动点满足：直线的斜率与直线的斜率之积为，则的取值范围为（    ）

A． B． C． D．

【答案】C

【分析】根据已知条件可得出、所满足的等式，求出的取值范围，结合二次函数的基本性质可求得的取值范围.

【详解】由题意可知，，整理得，

则，故，

因为，所以，所以，

即．

故选：C．

8．已知双曲线的左、右焦点分别为，一条渐近线为，过点且与平行的直线交双曲线于点，若，则双曲线的离心率为（    ）

A． B．

C． D．

【答案】C

【分析】由双曲线定义可得，根据平行关系可知，由余弦定理可构造齐次方程求得离心率.

【详解】设，则点位于第四象限，

由双曲线定义知：，；

设过点且与平行的直线的倾斜角为，则，，

；

在中，由余弦定理得：，

即，整理可得：，.

故选：C.

二、多选题

9．下列说法正确的是（    ）

A．直线必过定点

B．过点作圆的切线，切线方程为

C．经过点，倾斜角为的直线方程为

D．直线在x轴上的截距为，在y轴上的截距为1

【答案】AB

【分析】根据直线系的方程求解顶点即可判断A；结合点在圆上求解切线判断B；分和讨论判断C；直接求解直线在坐标轴上的交点坐标即可判断D.

【详解】解：对于A选项，，

故直线过与的交点，

所以，联立得，即直线必过定点，故正确；

对于B选项，点在上，圆心为，所以切线的斜率为，所以切线方程为，即，故正确；

对于C选项，经过点，倾斜角时，直线方程为，当时，直线方程为，故错误；

对于D选项，令得，令得，所以直线在x轴上的截距为，在y轴上的截距为，故错误.

故选：AB

10．如图，在三棱柱中，，，设，，，且向量与的夹角为45°，则（    ）

A．

B．与AC所成的角为60°

C．

D．当时，三棱锥的体积为定值

【答案】BD

【分析】对于A，由勾股定理可判断；

对于B，由题可知，，，，．根据空间向量的数量积以及向量的夹角运算可判断；

对于C，根据空间向量的线性运算可判断；

对于D，由已知得点P在直线上．从而得直线上的点到平面的距离相等，由此可判断．

【详解】解：对于A，∵，，∴，故A不正确；

对于B，由题可知，，，，．

∵，

∴，∴与AC所成的角为60°，故B正确；

对于C，，故C不正确；

对于D，∵，∴点P在直线上．由于平面，∴直线上的点到平面的距离相等，又的面积为定值，∴三棱锥的体积为定值，故D正确．

故选：BD．

11．双曲线具有如下光学性质：如图，是双曲线的左、右焦点，从右焦点发出的光线m交双曲线右支于点P，经双曲线反射后，反射光线n的反向延长线过左焦点．若双曲线C的方程为，下列结论正确的是（    ）

A．若，则

B．当n过时，光由所经过的路程为13

C．射线n所在直线的斜率为k，则

D．若，直线PT与C相切，则

【答案】CD

【分析】对于A：判断出，由定义和勾股定理联立方程组即可求得；对于B：利用双曲线的定义直接求得；对于C：先求出双曲线的渐近线方程，由P在双曲线右支上，即可得到n所在直线的斜率的范围；对于D：设直线PT的方程为.利用相切解得，进而求出.即可求出.

【详解】对于A：若，则.

因为P在双曲线右支上，所以.由勾股定理得：

二者联立解得：.故A错误；

对于B：光由所经过的路程为.

故B错误；

对于C：双曲线的方程为.设左、右顶点分别为A、B.如图示：

当与同向共线时，的方向为，此时k=0，最小.

因为P在双曲线右支上，所以n所在直线的斜率为.即.

故C正确.

对于D：设直线PT的方程为.

，消去y可得：.

其中，即，解得

代入，有，解得：x=9.

由P在双曲线右支上，即，解得：（舍去），所以.

所以.

故D正确

故选：CD

12．过椭圆的中心任作一直线交椭圆于P，Q两点，，是椭圆的左、右焦点，A，B是椭圆的左、右顶点，则下列说法正确的是（    ）

A．周长的最小值为18

B．四边形可能为矩形

C．若直线PA斜率的取值范围是，则直线PB斜率的取值范围是

D．的最小值为-1

【答案】AC

【分析】A由椭圆对称性及定义有周长为，根据椭圆性质即可判断；B根据圆的性质，结合椭圆方程与已知判断正误；C、D设，利用斜率两点式可得，进而判断C正误，应用向量数量积的坐标表示列关于的表达式，结合椭圆有界性求最值.

【详解】A：根据椭圆的对称性，，当PQ为椭圆的短轴时，有最小值8，所以周长的最小值为18，正确；

B：若四边形为矩形，则点P，Q必在以为直径的圆上，但此圆与椭圆无交点，错误；

C：设，则，因为直线PA斜率的范围是，所以直线PB斜率的范围是，正确；

D：设，则．因为，所以当时，最小值为，错误.

故选：AC．

三、填空题

13．已知点，，直线，若直线与直线平行，则______．

【答案】

【分析】根据两点坐标求得直线的斜率，根据直线方程求得直线的斜率，根据平行的必要条件得到关于的方程，求得的值，然后检验点（或点）不在直线上，进而得到答案.

【详解】直线的斜率为,直线的斜率为，由于直线与直线平行，所以，即，此时直线的方程为，

整理得：，经检验点（或点）不在直线上，所以当且仅当时，直线与直线平行，

故答案为：

14．双曲线的一条渐近线方程为，且焦点到渐近线的距离为2，则该双曲线的焦距为____________．

【答案】

【分析】根据渐近线方程可得的关系，然后根据焦点到渐近线的距离，结合点到直线的距离公式即可求得，从而求得，即可得到结果.

【详解】因为双曲线的渐近线方程为，

且其一条渐近线方程为，所以

由双曲线的对称性可知，两焦点到两渐近线的距离均相等，

取渐近线，焦点

则，所以，，即

所以焦距为

故答案为:

15．已知椭圆的中心在坐标原点，右焦点与圆的圆心重合，长轴长等于圆的直径，那么短轴长等于______．

【答案】

【分析】由于是圆，可得，通过圆心和半径计算，即得解

【详解】由于是圆，

即：圆

其中圆心为，半径为4

那么椭圆的长轴长为8，即，，，

那么短轴长为

故答案为：

16．四叶草也叫幸运草，四片叶子分别象征着：成功､幸福､平安､健康，表达了人们对美好生活的向往.梵克雅宝公司在设计四叶草吊坠的时候，利用了曲线方程（如图所示）进行图案绘制.试求曲线围成的封闭图形的面积___________.

【答案】

【分析】先对分情况讨论，去掉绝对值，然后结合方程表示的图形求解面积.

【详解】当时，方程可化为它表示圆心在，半径为

的圆在第一象限的部分；

当时，方程可化为它表示圆心在，半径为

的圆在第四象限的部分；

当时，方程可化为它表示圆心在，半径为

的圆在第二象限的部分；

当时，方程可化为它表示圆心在，半径为

的圆在第三象限的部分；

综上，四个部分都是半圆，并且它们正好围成了一个封闭的区域.

这个区域的面积可以割成四个半圆和一个正方形，其中正方形的边长就是半圆的直径.

所以总面积为.

故答案为：.

四、解答题

17．如图，在三棱锥中，点为棱上一点，且，点为线段的中点．

(1)以为一组基底表示向量；

(2)若，，，求．

【答案】(1)；

(2).

【分析】（1）直接利用向量的数乘运算及加减运算求解；

（2）由向量的单项式乘多项式及向量的数量积运算求解．

【详解】（1）∵为线段的中点，∴，

∵，∴，

∴

；

（2）

．

18．已知点，________，从条件①、条件②、条件③中选择一个作为已知条件补充在横线处，并作答．

(1)求直线的方程；

(2)求直线：关于直线的对称直线的方程．

条件①：点关于直线的对称点的坐标为；

条件②：点的坐标为，直线过点且与直线垂直；

条件③点的坐标为，直线过点且与直线平行．

注：如果选择多个条件分别解答，按第一个解答计分．

【答案】(1)

(2)

【分析】（1）计算直线的斜率，根据直线的平行或垂直关系得到斜率，代入点得到直线方程.

（2）计算直线的交点，在直线上取一点，求其关于对称的点，根据交点和对称点得到直线方程.

【详解】（1）选择条件：

因为点关于直线的对称点的坐标为，所以是线段的垂直平分线．

因为，所以直线的斜率为，又线段的中点坐标为，

所以直线的方程为，即．

选择条件：

因为，直线与直线垂直，所以直线的斜率为，

又直线过点，所以直线的方程为，即．

选择条件，

因为，直线与直线平行，所以直线的斜率为，

又直线过点，所以直线的方程为，即．

（2），解得，故，的交点坐标为，

因为在直线：上，设关于对称的点为，

则，解得，

直线关于直线对称的直线经过点，，代入两点式方程得，即，

所以：关于直线的对称直线的方程为．

19．如图，圆台上底面圆半径为1，下底面圆半径为为圆台下底面的一条直径，圆上点满足是圆台上底面的一条半径，点在平面的同侧，且.

(1)证明：平面平面；

(2)若圆台的高为2，求直线与平面所成角的正弦值.

【答案】(1)证明见解析

(2)

【分析】（1）取中点，四边形为平行四边形，从而得到，根据平面可得平面，从而得到需求证的面面垂直.

（2）建立如图所示的空间直角坐标系，求出及平面的法向量后可求线面角的正弦值.

【详解】（1）取中点，由题意，，

又，故.

又，故，

所以四边形为平行四边形，则.

由平面，故平面，

又面，故平面平面.

（2）以为坐标原点，的方向为轴的正方向，建立如图所示的空间直角坐标系.则有：，

故

设平面的法向量

而，

故，令，得

设所求角的大小为，则.

所以直线与平面所成角的正弦值为.

20．已知圆．

(1)若圆C被直线截得的弦长为8，求圆C的直径；

(2)已知圆C过定点P，且直线与圆C交于A，B两点，若，求a的取值范围．

【答案】(1)；

(2).

【分析】（1）根据弦长为8，利用弦心距、半径、半弦长之间的关系列出方程求解即可；

（2）求出动圆所过定点，再联立直线与圆的方程，求出交点坐标，由数量积的坐标运算列出不等式即可求解.

【详解】（1）依题意可知圆的圆心为，

到直线的距离，

因为圆被直线截得的弦长为8，所以，

解得，故圆的直径为.

（2）圆的一般方程为，

令，，解得，所以定点的坐标为.

联立解得或

所以，因为，所以.

又方程表示一个圆，所以，

所以的取值范围是.

21．已知抛物线的顶点为原点，焦点F在x轴的正半轴，F到直线的距离为.点为此抛物线上的一点，.直线l与抛物线交于异于N的两点A，B，且.

(1)求抛物线方程和N点坐标；

(2)求证：直线AB过定点，并求该定点坐标.

【答案】(1)，

(2)证明见解析，定点

【分析】（1）设抛物线的标准方程为，利用点到直线距离公式可求出，再利用焦半径公式可求出N点坐标；

（2）设直线的方程为，与抛物线联立，利用韦达定理计算，可得关系，然后代入直线方程可得定点.

【详解】（1）设抛物线的标准方程为，，其焦点为

则，

∴

所以抛物线的方程为.

，所以，所以.

因为，所以，所以.

（2）由题意知，直线的斜率不为0，设直线的方程为（），

联立方程得

设两个交点，（，）.

所以

所以，

即

整理得，此时恒成立，

此时直线l的方程为，可化为，

从而直线过定点.

22．已知，直线过椭圆的右焦点F且与椭圆交于A、B两点，l与双曲线的两条渐近线、分别交于M、N两点．

(1)若，且当轴时，△MON的面积为，求双曲线的方程；

(2)如图所示，若椭圆的离心率，且，求实数的值．

【答案】(1)；

(2).

【分析】（1）由题设可得、，结合三角形面积可得，由椭圆参数关系求a、b，即可写出双曲线方程.

（2）由椭圆离心率可得，进而可得双曲线渐近线，假设，写出、l方程，联立求N坐标，由向量的数量关系及向量坐标表示求A坐标，根据A在椭圆上求值.

【详解】（1）由题设，且双曲线的渐近线为，

当轴时，，又，△MON的面积为，

所以，故，而，可得，

所以双曲线的方程为.

（2）对于椭圆有，而，则，

不妨假设，则且l为，

所以，又，，

令，则，故，

所以，而在椭圆上，

则，整理得，

综上，可得.