2022-2023学年九年级上册数学人教版第二十二章二次函数（单元测试）

第二十二章二次函数（单元测试）2022-2023学年九年级上册数学人教版

一、单选题（本大题共12小题，每小题3分，共36分)。

1．抛物线的顶点坐标是（    ）

A． B． C． D．

2．如图，抛物线的对称轴为，下列结论正确的是（   ）

A． B．

C．当时，随的增大而减小 D．当时，随的增大而减小

3．在羽毛球比赛中，某次羽毛球的运动路线呈抛物线形，羽毛球距地面的高度与水平距离之间的关系如图所示，点B为落地点，且，，羽毛球到达的最高点到y轴的距离为，那么羽毛球到达最高点时离地面的高度为（    ）

A． B． C． D．

4．下列关于二次函数的图像和性质的叙述中，正确的是（    ）

A．点在函数图像上 B．开口方向向上

C．对称轴是直线 D．与直线有两个交点

5．抛物线经过点、，且与y轴交于点，则当时，y的值为（    ）

A． B． C． D．5

6．在平面直角坐标系中，将二次函数的图像向左平移2个单位长度，再向上平移1个单位长度，所得抛物线对应的函数表达式为（    ）

A． B． C． D．

7．已知抛物线的对称轴在轴右侧，现将该抛物线先向右平移3个单位长度，再向上平移1个单位长度后，得到的抛物线正好经过坐标原点，则的值是（    ）

A．或2 B． C．2 D．

8．关于二次函数，下列说法正确的是（    ）

A．函数图象的开口向下 B．函数图象的顶点坐标是

C．该函数有最大值，是大值是5 D．当时，y随x的增大而增大

9．已知二次函数的图象上有两点A（x1，2023）和B（x2，2023），则当时，二次函数的值是（   ）

A．2020 B．2021 C．2022 D．2023

10．抛物线y＝x2+3上有两点A（x1，y1），B（x2，y2），若y1＜y2，则下列结论正确的是(   )

A．0≤x1＜x2 B．x2＜x1≤0

C．x2＜x1≤0或0≤x1＜x2 D．以上都不对

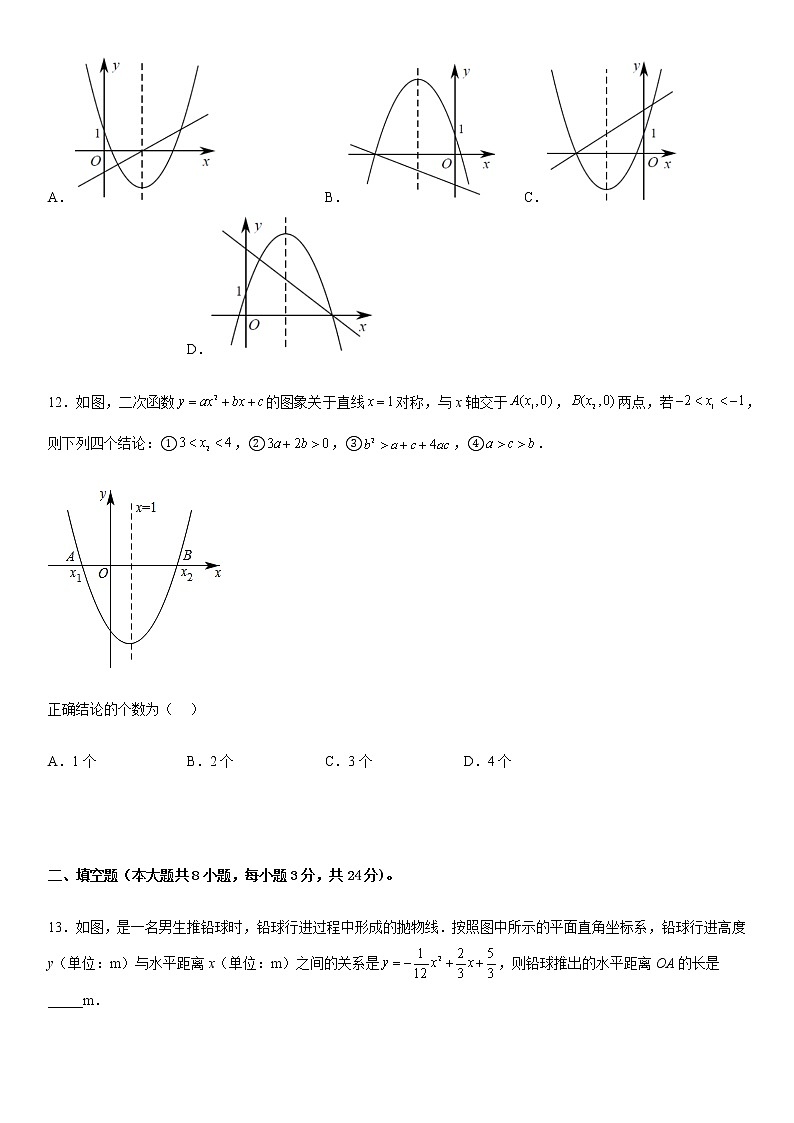
11．二次函数的图象与一次函数在同一平面直角坐标系中的图象可能是（    ）

A． B． C． D．

12．如图，二次函数的图象关于直线对称，与x轴交于，两点，若，则下列四个结论：①，②，③，④．

正确结论的个数为（    ）

A．1个 B．2个 C．3个 D．4个

二、填空题（本大题共8小题，每小题3分，共24分)。

13．如图，是一名男生推铅球时，铅球行进过程中形成的抛物线．按照图中所示的平面直角坐标系，铅球行进高度y（单位：m）与水平距离x（单位：m）之间的关系是，则铅球推出的水平距离OA的长是_____m．

14．如图，抛物线与轴交于点，与轴交于A，两点，则该抛物线的解析式是____．

15．把二次函数y=x2+4x+m的图像向上平移1个单位长度，再向右平移3个单位长度，如果平移后所得抛物线与坐标轴有且只有一个公共点，那么m应满足条件：________．

16．如图，抛物线y＝ax2与直线y＝bx+c的两个交点坐标分别为A(﹣3，6)，B(1，3)，则方程ax2﹣bx﹣c＝0的解是_________．

17．如图，二次函数的图像过点(－1，0)，对称轴为直线x=2，下列结论：①4a+b=0；②9a+c<3b；③8a+7b+2c>0；④若点A(－3，)、点B()、点C()在该函数图像上，则：⑤若方程的两根为，且，则其中正确的结论有__________． (只填序号)

18．二次函数的部分图象如图所示，由图象可知，方程的解为___________________；不等式的解集为___________________．

19．已知二次函数，当时，函数值y的最小值为1，则a的值为_______．

20．平面直角坐标系中，已知点，且实数m，n满足，则点P到原点O的距离的最小值为___________．

三、解答题（本大题共5小题，每小题8分，共40分)。

21．如图，抛物线y＝x2+x﹣2与x轴交于A、B两点，与y轴交于点C．

（1）求点A，点B和点C的坐标；

（2）抛物线的对称轴上有一动点P，求PB+PC的值最小时的点P的坐标．

22．某公司电商平台，在2021年五一长假期间，举行了商品打折促销活动，经市场调查发现，某种商品的周销售量y（件）是关于售价x（元/件）的一次函数，下表仅列出了该商品的售价x，周销售量y，周销售利润W（元）的三组对应值数据．

（1）求y关于x的函数解析式（不要求写出自变量的取值范围）；

（2）若该商品进价a（元/件），售价x为多少时，周销售利润W最大？并求出此时的最大利润；

（3）因疫情期间，该商品进价提高了m（元/件）（），公司为回馈消费者，规定该商品售价x不得超过55（元/件），且该商品在今后的销售中，周销售量与售价仍满足（1）中的函数关系，若周销售最大利润是4050元，求m的值．

23．如图，抛物线的顶点为A(h，－1)，与y轴交于点B，点F(2，1)为其对称轴上的一个定点．

（1）求这条抛物线的函数解析式；

（2）已知直线l是过点C(0，－3)且垂直于y轴的定直线，若抛物线上的任意一点P(m，n)到直线l的距离为d，求证：PF＝d；

（3）已知坐标平面内的点D(4，3)，请在抛物线上找一点Q，使△DFQ的周长最小，并求此时DFQ周长的最小值及点Q的坐标．

24．在平面直角坐标系xOy中，已知抛物线y=-x2+2mx+3m，点A（3，0）．

(1)当抛物线过点A时，求抛物线的解析式；

(2)证明：无论m为何值，抛物线必过定点D，并求出点D的坐标；

(3)在（1）的条件下，抛物线与y轴交于点B，点P是抛物线上位于第一象限的点，连接AB，PD交于点M，PD与y轴交于点N．设S=S△PAM－S△BMN，问是否存在这样的点P，使得S有最大值？若存在，请求出点P的坐标，并求出S的最大值；若不存在，请说明理由．

25．如图，抛物线经过点，点，与y轴交于点C，抛物线的顶点为D．

(1)求抛物线的解析式；

(2)抛物线上是否存在点P，使的面积是面积的4倍，若存在，请直接写出点P的坐标：若不存在，请说明理由．

参考答案：

1．B

2．C

3．D

4．D

5．A

6．B

7．B

8．D

9．C

10．D

11．A

12．B

13．10

14．

15．m>3

16．x1＝﹣3，x2＝1

17．①②③⑤

18．     ，     或

19．

20．

21．（1）A（﹣2，0），B（1，0），C（0，﹣2）．（2）P（，）

22．（1）；（2）售价60元时，周销售利润最大为4800元；（3）

23．（1）；（2）见解析；（3），

24．(1)y=-x2+2x+3；

(2)证明见解析，；

(3)存在，点的坐标是（1，4），．

25．(1)

(2)存在，，