

还剩13页未读,
继续阅读
第01讲 集合 期末大总结(解析版) 试卷
展开
这是一份第01讲 集合 期末大总结(解析版),共16页。
第1讲 集合 期末大总结
目 录 速 览
第一部分:必会知识结构导图
第二部分:考点梳理知识方法技巧大总结
第三部分:必会技能常考题型及思想方法大归纳
必会题型一:集合的含义与表示
必会题型二:集合间的基本关系
必会题型三:集合的基本运算
必会题型四:Venn图法解决集合运算问题
必会题型五:分类讨论法解决元素与集合关系问题
必会题型六:根据集合包含关系求参数值或范围
第一部分:知识结构导图速看
第二部分:考点梳理知识方法技巧大总结
1.集合与元素的概念
(1)集合:一般地,指定的某些对象的全体称为集合.集合常用大写字母A,B,C,D,…标记.
(2)元素:集合中的每个对象叫作这个集合的元素.元素常用小写字母a,b,c,d,…标记.
2.元素与集合的关系
(1)属于:若a在集合A中,就说a属于集合A,记作a∈A.
(2)不属于:若a不在集合A中,就说a不属于集合A,记作a∉A.
3.集合中元素的特性
(1)确定性;(2)互异性(元素互不相同);
(3)无序性:如{1,2,3}和{3,2,1}表示同一个集合.
4.集合的表示
(1)列举法:列举法是把集合中的元素一一列举出来并用大括号“{}”括起来的方法(元素之间用“,”隔开),如{1,2,3}.
(2)描述法:用确定的条件表示某些对象是否属于这个集合的方法叫描述法。它的一般形式为{x∈A|p(x)},如{(x,y)|xy=0}、{x|(x+1)(x-3)=0}、{y|y=x2}.
5.常用数集及表示符号:
自然数集N;正整数集N*或N+;整数集Z;有理数集Q;实数集R。
6.集合的分类
(1)有限集:我们把含有限个元素的集合叫有限集.
(2)无限集:含无限个元素的集合叫无限集.
(3)空集:我们把不含有任何元素的集合叫作空集,记作∅.
7.Venn图:用平面上封闭曲线的内部代表集合这种图称为Venn图(可以是圆,椭圆,矩形等封闭曲线)。
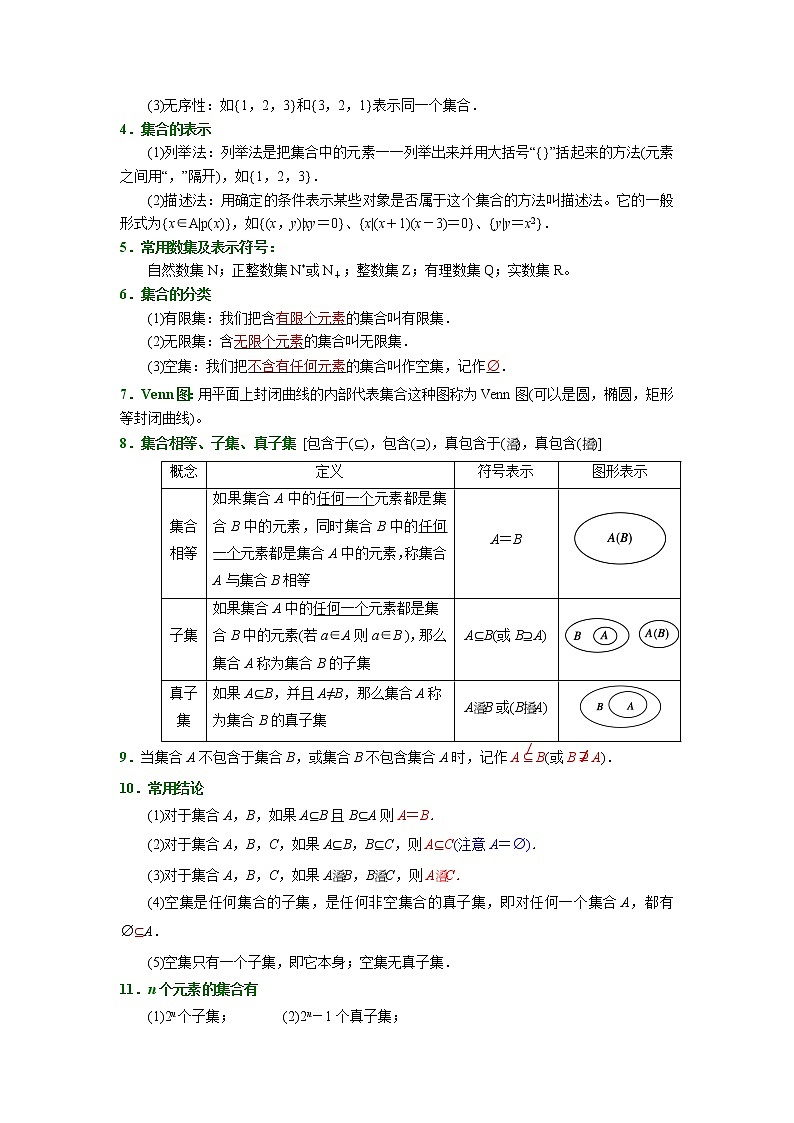
8.集合相等、子集、真子集 [包含于(⊆),包含(⊇),真包含于(),真包含()]
概念
定义
符号表示
图形表示
集合相等
如果集合A中的任何一个元素都是集合B中的元素,同时集合B中的任何一个元素都是集合A中的元素,称集合A与集合B相等
A=B
子集
如果集合A中的任何一个元素都是集合B中的元素(若a∈A则a∈B ),那么集合A称为集合B的子集
A⊆B(或B⊇A)
真子集
如果A⊆B,并且A≠B,那么集合A称为集合B的真子集
AB或(BA)
9.当集合A不包含于集合B,或集合B不包含集合A时,记作AB(或BA).
10.常用结论
(1)对于集合A,B,如果A⊆B且B⊆A则A=B.
(2)对于集合A,B,C,如果A⊆B,B⊆C,则A⊆C(注意A=∅).
(3)对于集合A,B,C,如果AB,BC,则AC.
(4)空集是任何集合的子集,是任何非空集合的真子集,即对任何一个集合A,都有∅⊆A.
(5)空集只有一个子集,即它本身;空集无真子集.
11.n个元素的集合有
(1)2n个子集; (2)2n-1个真子集;
(3)2n-1个非空子集;(4)2n-2个非空真子集.
12.并集、交集与补集
并集A∪B
交集A∩B
补集∁U
文字符号语言
集合A和B的元素合并在一起组成的集合。
A∪B={x|x∈A或x∈B}
集合A和B的公共元素组成的集合。
A∩B={x|x∈A且x∈B}
全集U中不属于A的所有元素构成的集合。
∁U A={x|x∈U且x∉A}
图形语言
常用运算
A∪∅=A;
A∪B⊇A;B⊆A∪B
A∪B=A⇔B⊆A
(A∪B)∪C=A∪(B∪C);
A∩∅=∅;
A∩B⊆A;A∩B⊆B;
A∩B=A⇔A⊆B
(A∩B)∩C=A∩(B∩C);
∁UU=∅;∁U∅=U;
∁U(∁UA)=A;
A∪∁UA=U;
A∩∁UA=∅
A⊆B⇔∁UB⊆∁UA.
13.知识拓展
(1)集合的分配律:A∩(B∪C)=(A∩B)∪(A∩C);A∪(B∩C)=(A∪B)∩(A∪C)
(2)德·摩根定律:∁U(A∩B)=(∁UA)∪(∁UB) [“交的补”等于“补的并”];
∁U(A∪B)=(∁UA)∩(∁UB) [“并的补”等于“补的交”]
德·摩根法则的理解如图:
(3)全集与补集各部分的韦恩图表示(如图)
(4)容斥定律(求集合元素的个数):设有限集A的元素个数为card(A),例如集合A={a,b,c},则card(A)=3;则在求集合元素个数时常用到以下公式及图形解释(如图)
①card(A∪B)=card(A)+card(B)-card(A∩B)
②card(A∪B∪C)=card(A)+card(B)+card(C)-card(A∩B)-card(A∩B)-card(B∩C)+card(A∩B∩C)
第三部分:必会技能常考题型及思想方法大归纳
必会题型一:集合的含义与表示
1. (2022·重庆市第二十九中学校高一期中)已知集合A={0,1,2},B={x|x=ab,a∈A,b∈A},则集合B中有( )个元素.
A.1 B.2 C.3 D.4
【答案】D
【分析】根据集合B的定义,求得集合B,即可求得结果.
【解析】根据题意可得,集合B={0,1,2,4},故其元素有4个.
故选:D.
2.(2022·海南华侨中学高一期中)已知集合A=xx=2k,k∈Z,B=xx=2m+1,m∈Z,C=xx=4n+1,n∈Z,若a∈A,b∈B,则必有( )
A.a+b∈A B.a+b∈B
C.a+b∈C D.a+b不属于集合A、B、C中的任何一个
【答案】B
【分析】设出a,b的表示形式,计算a+b后比较各集合的代表元形式可得.
【解析】由题意设a=2k,b=2m+1,其中k,m都是整数,
则a+b=2k+2m+1=2(k+m)+1,其中k+m是整数,可以是奇数也可以是偶数,
∴a+b∈B,
故选:B.
3.[多选](2022·贵州·贵阳一中高一阶段练习)在整数集Z中,被5除所得余数为k的所有整数组成一个“类”,记为[k],即[k]={5n+k|n∈Z},k=0,1,2,3,4. 下列结论正确的是( )
A.2 022∈[2]
B.-3∈[3]
C.Z=0∪1∪2∪3∪4
D.整数a,b属于同一个“类”的充要条件是a−b∈[0]
【答案】ACD
【分析】根据“类”的定义对选项进行分析,从而确定正确答案.
【解析】2022=404×5+2,所以2022∈2,A选项正确.
−3=−5+2,所以−3∈2,B选项错误.
整数是由5的倍数、5的倍数加1、5的倍数加2、5的倍数加3、5的倍数加4所构成,
所以Z=0∪1∪2∪3∪4,C选项正确.
当a,b属于同一个“类”时,设a=5n1+k,b=5n2+k,n1,n2∈Z,k=0,1,2,3,4,
所以a−b=5n1−n2∈0;
当a−b∈[0]时,a−b=5n,n∈Z,所以a=5n+b,a=5n+b=b,
即a被5除所得余数和b被5除所得余数相等,也即a,b属于同一个“类”.
综上所述,整数a,b属于同一个“类”的充要条件是a−b∈[0],D选项正确.
故选:ACD
4.(2022·海南华侨中学高一期中)设集合A=−1,0,1,集合B=x∈N|6x+1∈N
(1)用列举法写出集合B
(2)定义:A∗B=x,yx∈A∩B,y∈A∪B,求A∗B中元素的个数.
【答案】(1)B=0,1,2,5 (2)10
【分析】(1)由x∈N,6x+1∈N,解得x;
(2)先求出A∩B=0,1,A∪B=−1,0,1,2,5,根据定义求出A∗B,继而得解.
【解析】(1)由x∈N,6x+1∈N,所以x可以取0,1,2,5,所以B=0,1,2,5.
(2)由题意可知:B=0,1,2,5.
∴A∩B=0,1,A∪B=−1,0,1,2,5
∵A∗B=(x,y)x∈A∩B,y∈A∪B
∴A∗B=(0,−1),0,0,0,1,0,2,0,5,1,−1,1,0,1,1,1,2,1,5.
∴A∗B中元素的个数为10.
必会题型二:集合间的基本关系
1.(2022·上海市彭浦中学高一期中)下列表示错误的是( )
A.0∉∅ B.∅⊆1,2
C.x,y2x+y=103x−y=5=3,4 D.若A⊆B,则A∪B=B
【答案】C
【分析】由元素与集合的关系可判断A;由集合与集合的包含关系可判断B;由描述法可判断C;由集合的包含关系与并集的定义可判断D
【解析】对于A:因为空集没有任何元素,故0∉∅,故A正确;
对于B:因为空集是任何集合的子集,故∅⊆1,2,故B正确;
对于C:x,y2x+y=103x−y=5表示2x+y=10与3x−y=5的交点所构成的集合,
所以x,y2x+y=103x−y=5=3,4,故C错误;
对于D:若A⊆B,则A∪B=B,故D正确;
故选:C
2.[多选]已知集合A=0,a+b,ab,A=2,2-b,c若A=B,则a+b+c的值可能为( )
A.32 B.2 C.232 D.12
【答案】ABD
【分析】根据A=B,得到2-b=0或c=0,分类讨论得到a的值,根据元素的互异性,舍去不合要求的解,求出a+b+c的值.
【解析】因为A=B,所以2-b=0或c=0.
①当b=2时,A=0,a+2,a2,B=2,0,c,
所以a+2=2或a2=2,得a=0或4.
当a=0时,A=0,2不合题设,舍去.
当a=4时,A=0,6,2,c=6,此时a+b+c=12.
②当c=0时,A=0,a+b,ab,B=2,2-b,0,
所以a+b=2ab=2-b或a+b=2-bab=2,解得:a=0b=2或a=1b=1或a=1b=12
当a=0时,A=0,2不合题设,舍去.
当a=1b=1时,A=B=0,2,1,此时a+b+c=2.
当a=1b=12时,A=B=0,32,2,此时a+b+c=32.
故选:ABD
3.已知集合A满足1,2⊆A⊆1,2,3,4,5,2,3⊆A⊆1,2,3,5,6,则满足条件的集合A的个数为( )
A.8个 B.4个 C.2个 D.1个
【答案】C
【分析】根据给定的条件,确定集合A中元素即可求解作答.
【解析】因1,2⊆A⊆1,2,3,4,5,2,3⊆A⊆1,2,3,5,6,则有1,2,3都是集合A中元素,4,6都不在A中,5可以在A中,
因此集合A可以是{1,2,3}或{1,2,3,5},
所以满足条件的集合A的个数为2.
故选:C
4.(2022·上海·华师大二附中高一期中)已知集合A=xax2+3x−2=0有且仅有两个子集,则满足条件的实数a组成的集合是___________
【答案】−98,0
【分析】根据集合A的子集的个数得到集合A中只有一个元素,然后分a=0和a≠0两种情况求解即可.
【解析】因为集合A有且仅有两个子集,所以集合A中只有一个元素,即方程ax2+3x−2=0只有一个解,
当a=0时,3x−2=0,只有一个解,满足要求;
当a≠0时,Δ=9+8a=0,解得a=−98,所以a=−98或0.
故答案为:−98,0.
必会题型三:集合的基本运算
1.(广东省深圳科学高中2022-2023学年高一上学期期中数学试题)若全集U={1,2,3,4,5,6,7,8,9},A={1,2,3,5},B={1,2,4,6,7,8},则∁UA∪∁UB=( )
A.∅ B.{3,4,5,6,7,8,9} C.{9} D.{1,2}
【答案】B
【分析】由补集与并集的概念求解,
【解析】由题意得∁UA={4,6,7,8,9},∁UB={3,5,9},∁UA∪∁UB={3,4,5,6,7,8,9}
故选:B
2.(2022·陕西·渭南市瑞泉中学高一阶段练习)已知集合M=x−1
【答案】A
【分析】由定义域得到不等式,解不等式求出N=−1,32,从而求出交集.
【解析】3+x−2x2≥0,解得:−1≤x≤32,所以N=−1,32,
所以M∩N=−1,1∩−1,32=−1,1.
故选:A
3.[多选](辽宁省名校联盟2022-2023学年高一11月选科适应性考试数学试题)对于集合M,N,定义M−N={xx∈M且x∉N},设全集U=x∈Z−3
C.M−N={−2} D.∁U(N−M)={−2,−1,2,3}
【答案】CD
【分析】根据集合的新定义以及交并补运算,即可求解.
【解析】根据集合的互异性,即可判断A错,
M的非空真子集个数为23−2=6,即可判断B错,
根据M−N={xx∈M且x∉N},即可判断C对,
N−M={0,1},∁U(N−M)={−2,−1,2,3},即可判断D对,
故选:CD.
4.(湖南省衡阳市田家炳实验中学2022-2023学年高一上学期期中数学试题)已知集合A=x3
(2)求:∁RA∪B,A∪(∁RB).
【答案】(1)xx<2或x>10,xx≤3或x≥5;
(2)R,xx<2或310
【分析】根据集合的交、并、补运算求解即可.
【解析】(1)由题意,A∪B={x|2≤x≤10},A∩B={x|3
(2)由题意,∁RA =xx≤3或x≥5,∁RB= xx<2或x>10,
故∁RA∪B=R,A∪(∁RB)= xx<2或310.
5.(浙江省台州市三门第二高级中学2022-2023学年高一上学期第一次月考数学试题)已知集合A=xa−1
(2)若A∩B=A,求实数a的取值范围.
【答案】(1)A∪B=x−2≤x<7,∁RA∩B=x−2≤x≤1
(2)a≤−4或−1≤a≤12
【分析】(1)代入a=2,得到集合A,根据集合运算的概念求解即可;
(2)由已知可得,A⊆B,对A=∅与A≠∅分别求解.
【解析】(1)当a=2时,集合A=x1
又U=R,∴∁RA=x|x≤1或x≥7,
∴∁RA∩B=x−2≤x≤1.
(2)若A∩B=A,则A⊆B,
当a−1≥2a+3,即a≤−4时,A=∅,满足题意;
当A≠∅,即a>−4时,应满足a−1≥−22a+3≤4,解得−1≤a≤12;
综上知,实数a的取值范围是a≤−4或−1≤a≤12.
必会题型四:Venn图法解决集合运算问题
1.(2022·陕西·交大附中高一期中)已知集合A=x∈N1≤x≤6,B=xx2−x−6≤0,则如图中阴影部分表示的集合为( ).
A.0,1,2 B.1,2,3 C.−3,0,1,2 D.−2,0,1,2,3
【答案】B
【分析】由自然数集N的定义化简集合A,解二次不等式化简集合B,由韦恩图可知阴影部分表示的集合为A∩B,由此得解.
【解析】易知A=x∈N1≤x≤6=1,2,3,4,5,6,
由x2−x−6≤0得x−3x+2≤0,故−2≤x≤3,则B=x−2≤x≤3,
由韦恩图可知阴影部分表示的集合为A∩B,而A∩B=1,2,3,
所以图中阴影部分表示的集合为1,2,3.
故选:B.
2.(重庆市璧山区2022-2023学年高一上学期10调研数学试题)图中阴影部分表示的集合为( )
A.∁UA∩B B.A∩∁UB C.∁UA∩∁UB D.∁U(A∩B)
【答案】A
【分析】根据集合的交并补运算逐个选项验证即可.
【解析】根据补集和交集的概念可知A选项的∁UA∩B符合题意;
由图可知,阴影部分为集合B的子集,而∁UB不是B的子集,故排除选项B、C;
∁U(A∩B)表示的区域如图:
所以D不符题意;
故选:A.
3.[多选](江苏省苏州市第五中学2022-2023学年高一上学期10月阶段性测试数学试题)正确表示图中阴影部分的是( )
A.∁UM∩∁UN B.∁UM∪N
C.∁UM∩N D.∁UM∪N
【答案】AD
【分析】根据阴影位于M与N并集的外部即可作出判断.
【解析】根据图中阴影可知,∁UM∪N符合题意,
又∁UM∪N=∁UM∩∁UN.
故选:AD
4.某年级举行数学、物理、化学三项竞赛,共有80名学生参赛,其中参加数学竞赛有40人,参加物理竞赛有45人,参加化学竞赛有30人,同时参加物理、化学竞赛有15人,同时参加数学、物理竞赛有20人,同时参加数学、化学竞赛有10人,这个年级三个学科竞赛都参加的学生共有______名.
【答案】10
【分析】利用容斥原理即可求解.
【解析】设三个学科竞赛都参加的学生为x人,
结合已知条件可知,
只参加物理、化学两个科目竞赛的学生为15−x人,
只参加数学、物理两个科目竞赛的学生为20−x人,
只参加数学、化学两个科目竞赛的学生为10−x人,
只参加物理竞赛的学生为45−(15−x)−x−(20−x)=10+x人,
只参加化学竞赛的学生为30−(15−x)−x−(10−x)=5+x人,
只参加数学竞赛的学生为40−(20−x)−x−(10−x)=10+x人,
如下图所示:
故45−20−15−x+40−20−10−x+30+20−x=80,解得x=10,
故都参加的学生人数为10人,
故答案为:10.
必会题型五:分类讨论法解决元素与集合关系问题
1.(北京市第十五中学南口学校2022-2023学年高一上学期期中考试数学试题)已知M=1,2,a2−3a−1,N=1,3,且N⫋M,则a的值为( )
A.−1 B.4
C.−1或4 D.1或−4
【答案】C
【分析】根据集合间的关系和元素与集合的关系,可知a2−3a−1=3,解方程即可得出答案.
【解析】因为M=1,2,a2−3a−1,N=1,3,且N⫋M,
所以a2−3a−1=3,解得:a=−1或a=4,
故选:C.
2.[多选](四川省成都市树德中学2022-2023学年高一上学期10月月考数学试题)下列四个命题:其中不正确的命题为( )
A.已知集合A=yy=x2+1,集合B=xy=x2+1,则A∩B=∅
B.集合x∈N|5x+1∈N中有两个元素
C.由方程x2−2x+1=0的所有实根构成的集合中的元素之和为2
D.记A=x|x=2k+1,k∈Z,B=x|x=4n±1,n∈Z,则A=B
【答案】AC
【分析】利用集合的定义可判断对错.
【解析】A=y|y≥1,B=R,A∩B=x|x≥1,所以A选项错误;
因为集合x∈N|5x+1∈N=0,4,所以B选项正确;
由于x|x2−2x+1=0=1,集合中只有一个元素,和为1,所以C选项错误;
对于集合A,当k=2n时,x=4n+1,n∈Z,当k=2n−1时,x=4n−1,n∈Z,即A=x|x=4n±1,n∈Z=B,所以D选项正确.
故选:AC.
3.(河南省南阳市六校2022-2023学年高一上学期期中考试数学试题)已知集合A=1,2,3,B=1,m,n,若2−m∈A,n+2∈A,则m+n=______.
【答案】−1
【分析】首先利用集合与元素的关系和集合元素的特征得到m=0n=−1或m=−1n=0,即可得到答案.
【解析】因为2−m∈A,所以2−m=1或2−m=2或2−m=3,
解得m=1或m=0或m=−1,
因为n+2∈A,所以n+2=1或n+2=2或n+2=3,
解得n=−1或n=0或n=1,
又因为B={1,m,n},所以m=0n=−1或m=−1n=0,即m+n=−1.
故答案为:−1
4.(1)设集合A={a2,a+1,−1},B={2a-1,|a-2|,3a2+4},A∩B=−1,求实数a的值.
(2)设集合A=x2,2x−1,−4,B=x−5,1−x,9,若A∩B=9,求实数x的值.
【答案】(1)a=0;(2)x=−3
【分析】根据A∩B的结果,对A、B的元素分类讨论即可
【解析】(1)∵A∩B=−1,∴−1∈B,而|a-2|≥0,3a2+4>0,∴2a-1=-1,则a=0,
此时A={0,1,-1},B={-1,2,4},A∩B=−1,符合题意.
故a=0;
(2)因为A=x2,2x−1,−4,B=x−5,1−x,9,A∩B=9,
若x2=9,则x=±3,
当x=3时,x−5=1−x=−2,不满足题意;
当x=−3时,A={9,−7,−4},B={−8,4,9},A∩B=9,满足题意;
若2x−1=9,则x=5,此时A=25,9,−4,B=0,−4,9,则A∩B={9,−4},不满足题意;
综上,x=−3.
必会题型六:根据集合包含关系求参数值或范围
1. (山东省菏泽市2022-2023学年高一上学期期中数学试题)设集合A=x−1≤x≤4,集合B=xx≥a,若A⊆B,则a的取值范围为( )
A.a≥4 B.−1≤a≤4
C.a<−1 D.a≤−1
【答案】D
【分析】根据集合的包含关系即可得解.
【解析】因为集合A=x−1≤x≤4,集合B=xx≥a,A⊆B,
所以a≤−1.
故选:D.
2.(辽宁省朝阳市建平县实验中学2022-2023学年高一上学期第一次月考数学试题)集合A=xx<−1或x≥3,B=xax+1≤0若B⊆A,则实数a的取值范围是( )
A.−13,1 B.−13,1
C.−∞,1∪0,+∞ D.−13,0∪0,1
【答案】A
【分析】根据B⊆A,分B=∅和B≠∅两种情况讨论,建立不等关系即可求实数a的取值范围.
【解析】∵B⊆A,
∴①当B=∅时,即ax+1≤0无解,此时a=0,满足题意.
②当B≠∅时,即ax+1≤0有解,
当a>0时,可得x≤−1a,
要使B⊆A,则需要a>0−1a<−1,解得0
要使B⊆A,则需要a<0−1a≥3,解得−13≤a<0,
综上,实数a的取值范围是−13,1.
故选:A.
3.(辽宁省朝阳市建平县实验中学2022-2023学年高一上学期第一次月考数学试题)已知集合A=x2a+1≤x≤3a−5,B={xx<−1或x>16} .
(1)若A为非空集合,求实数a的取值范围;
(2)若A∩B=A,求实数a的取值范围.
【答案】(1)a≥6
(2)a<6或a>152
【分析】(1)由条件可知,2a+1≤3a−5,即可求解不等式;
(2)分A=∅和A≠∅两种情况,列不等式求解.
【解析】(1)若A为非空集,则2a+1≤3a−5,解得:a≥6;
(2)若A∩B=A,则A⊆B,
当A=∅时,2a+1>3a−5,解得:a<6,
当A≠∅时,2a+1≤3a−53a−5<−1 ,解得:∅
或2a+1≤3a−52a+1>16,解得:a>152
所以实数a的取值范围是a<6或a>152
4.(山东省青岛市青岛第二中学2022-2023学年高一上学期期中数学试题)已知集合.A=x|a−2≤x≤a+2,B={x|x≤−1或x≥2}.
(1)当a=3时,求A∩B,A∪∁RB;
(2)若A∪B=R,求实数a的取值范围
【答案】(1)A∩B={x|2≤x≤5},A∪∁RB= {x−1
【分析】(1)应用集合的交、并、补运算求集合即可;
(2)根据并集结果得a−2≤−1a+2≥2,即可求参数范围.
【解析】(1)a=3时,A={x|1≤x≤5},所以A∩B={x|2≤x≤5},
因为∁RB= x−1
5.(江苏省苏州市吴县中学教育集团2022-2023学年高一上学期10月学业质量阳光指标调研数学试题)设全集为U=R,集合A={x|−2
(1)求如图阴影部分表示的集合;
(2)已知集合C={x|a0},若B∩C=∅,求实数a的取值范围.
【答案】(1)x|−2
(2)依题意可得a>02a≤6,解得即可.
【解析】(1)解:因为A={x|−2
所以图中阴影部分表示∁AA∩B=x|−20},B={x|x≤−3或x≥6}且B∩C=∅,
所以a>02a≤6,解得0
(1)若a=−1,求A∪∁RB;
(2)若A∩B=∅,求a的取值范围.
【答案】(1)A∪CRB=x−2≤x≤5
(2)x−12≤a≤2或a>3
【分析】(1)根据题意,先求出集合A的补集,再利用集合的并集运算求解即可;
(2)根据集合的包含关系分A=∅和A≠∅两种情况进行讨论即可求解.
【解析】(1)若a=−1,则集合A=x−2≤x≤2,
所以∁RB=x−1≤x≤5,
所以A∪CRB=x−2≤x≤5;
(2)因为集合A=x2a≤x≤a+3,B={x|x<−1或x>5},
因为A∩B=∅,所以分以下两种情况:
若A=∅,即2a>a+3,解得a>3,满足题意,
若A≠∅,则2a≥−1a+3≤52a≤a+3
解得−12≤a≤2,
综上所述a的取值范围为x−12≤a≤2或a>3
7.已知A=xx2−2x−3≤0,B=xx−a≤1,a∈R.
(1)若A∪B=A,求出实数a的取值范围;
(2)若a∈A,求A∩B.
【答案】(1)0≤a≤2
(2)答案见解析
【分析】(1)求出集合AB,然后根据并集结果列不等式求解即可;
(2)分a−1<−1
B=xx−a≤1,a∈R=−1+a,1+a
∵A∪B=A,∴B⊆A∴−1+a≥−11+a≤3
解得0≤a≤2
(2)由(1)A=−1,3,B=−1+a,1+a,a∈−1,3,
当a−1<−1
(1)若a=1,求A∪B;
(2)求实数a的取值范围,使___________成立.
从①A⊆∁RB,②B⊆∁RA,③∁RA∩B=∅中选择一个填入横线处求解.
注:如果选择多个条件分别解答,按第一个解答计分.
【答案】(1)x0
选2,a≤0或a≥6;
选3,2≤a≤4.
【分析】(1)根据对数函数的单调性求出集合A,根据一元二次不等式的解法求出集合B,结合并集的概念和运算即可得出结果;
(1)根据(1)和补集的概念和运算求出∁RA和∁RB,利用集合间的包含关系和交并补的运算即可求出对应条件的参数.
【解析】(1)A={xlog2(x−1)<2}={x0
若选①,A⊆∁RB,则a+1≤1或a−1≥5,
解得a≤0或a≥6,所以a的取值范围为a≤0或a≥6;
若选②,B⊆∁RA,则a+1≤1或a−1≥5,
解得a≤0或a≥6,所以a的取值范围为a≤0或a≥6;
若选③,(∁RA)∩B=∅,则1≤a−1a+1≤5,
解得2≤a≤4,所以a的取值范围为2≤a≤4.
第1讲 集合 期末大总结
目 录 速 览
第一部分:必会知识结构导图
第二部分:考点梳理知识方法技巧大总结
第三部分:必会技能常考题型及思想方法大归纳
必会题型一:集合的含义与表示
必会题型二:集合间的基本关系
必会题型三:集合的基本运算
必会题型四:Venn图法解决集合运算问题
必会题型五:分类讨论法解决元素与集合关系问题
必会题型六:根据集合包含关系求参数值或范围
第一部分:知识结构导图速看
第二部分:考点梳理知识方法技巧大总结
1.集合与元素的概念
(1)集合:一般地,指定的某些对象的全体称为集合.集合常用大写字母A,B,C,D,…标记.
(2)元素:集合中的每个对象叫作这个集合的元素.元素常用小写字母a,b,c,d,…标记.
2.元素与集合的关系
(1)属于:若a在集合A中,就说a属于集合A,记作a∈A.
(2)不属于:若a不在集合A中,就说a不属于集合A,记作a∉A.
3.集合中元素的特性
(1)确定性;(2)互异性(元素互不相同);
(3)无序性:如{1,2,3}和{3,2,1}表示同一个集合.
4.集合的表示
(1)列举法:列举法是把集合中的元素一一列举出来并用大括号“{}”括起来的方法(元素之间用“,”隔开),如{1,2,3}.
(2)描述法:用确定的条件表示某些对象是否属于这个集合的方法叫描述法。它的一般形式为{x∈A|p(x)},如{(x,y)|xy=0}、{x|(x+1)(x-3)=0}、{y|y=x2}.
5.常用数集及表示符号:
自然数集N;正整数集N*或N+;整数集Z;有理数集Q;实数集R。
6.集合的分类
(1)有限集:我们把含有限个元素的集合叫有限集.
(2)无限集:含无限个元素的集合叫无限集.
(3)空集:我们把不含有任何元素的集合叫作空集,记作∅.
7.Venn图:用平面上封闭曲线的内部代表集合这种图称为Venn图(可以是圆,椭圆,矩形等封闭曲线)。
8.集合相等、子集、真子集 [包含于(⊆),包含(⊇),真包含于(),真包含()]
概念
定义
符号表示
图形表示
集合相等
如果集合A中的任何一个元素都是集合B中的元素,同时集合B中的任何一个元素都是集合A中的元素,称集合A与集合B相等
A=B
子集
如果集合A中的任何一个元素都是集合B中的元素(若a∈A则a∈B ),那么集合A称为集合B的子集
A⊆B(或B⊇A)
真子集
如果A⊆B,并且A≠B,那么集合A称为集合B的真子集
AB或(BA)
9.当集合A不包含于集合B,或集合B不包含集合A时,记作AB(或BA).
10.常用结论
(1)对于集合A,B,如果A⊆B且B⊆A则A=B.
(2)对于集合A,B,C,如果A⊆B,B⊆C,则A⊆C(注意A=∅).
(3)对于集合A,B,C,如果AB,BC,则AC.
(4)空集是任何集合的子集,是任何非空集合的真子集,即对任何一个集合A,都有∅⊆A.
(5)空集只有一个子集,即它本身;空集无真子集.
11.n个元素的集合有
(1)2n个子集; (2)2n-1个真子集;
(3)2n-1个非空子集;(4)2n-2个非空真子集.
12.并集、交集与补集
并集A∪B
交集A∩B
补集∁U
文字符号语言
集合A和B的元素合并在一起组成的集合。
A∪B={x|x∈A或x∈B}
集合A和B的公共元素组成的集合。
A∩B={x|x∈A且x∈B}
全集U中不属于A的所有元素构成的集合。
∁U A={x|x∈U且x∉A}
图形语言
常用运算
A∪∅=A;
A∪B⊇A;B⊆A∪B
A∪B=A⇔B⊆A
(A∪B)∪C=A∪(B∪C);
A∩∅=∅;
A∩B⊆A;A∩B⊆B;
A∩B=A⇔A⊆B
(A∩B)∩C=A∩(B∩C);
∁UU=∅;∁U∅=U;
∁U(∁UA)=A;
A∪∁UA=U;
A∩∁UA=∅
A⊆B⇔∁UB⊆∁UA.
13.知识拓展
(1)集合的分配律:A∩(B∪C)=(A∩B)∪(A∩C);A∪(B∩C)=(A∪B)∩(A∪C)
(2)德·摩根定律:∁U(A∩B)=(∁UA)∪(∁UB) [“交的补”等于“补的并”];
∁U(A∪B)=(∁UA)∩(∁UB) [“并的补”等于“补的交”]
德·摩根法则的理解如图:
(3)全集与补集各部分的韦恩图表示(如图)
(4)容斥定律(求集合元素的个数):设有限集A的元素个数为card(A),例如集合A={a,b,c},则card(A)=3;则在求集合元素个数时常用到以下公式及图形解释(如图)
①card(A∪B)=card(A)+card(B)-card(A∩B)
②card(A∪B∪C)=card(A)+card(B)+card(C)-card(A∩B)-card(A∩B)-card(B∩C)+card(A∩B∩C)
第三部分:必会技能常考题型及思想方法大归纳
必会题型一:集合的含义与表示
1. (2022·重庆市第二十九中学校高一期中)已知集合A={0,1,2},B={x|x=ab,a∈A,b∈A},则集合B中有( )个元素.
A.1 B.2 C.3 D.4
【答案】D
【分析】根据集合B的定义,求得集合B,即可求得结果.
【解析】根据题意可得,集合B={0,1,2,4},故其元素有4个.
故选:D.
2.(2022·海南华侨中学高一期中)已知集合A=xx=2k,k∈Z,B=xx=2m+1,m∈Z,C=xx=4n+1,n∈Z,若a∈A,b∈B,则必有( )
A.a+b∈A B.a+b∈B
C.a+b∈C D.a+b不属于集合A、B、C中的任何一个
【答案】B
【分析】设出a,b的表示形式,计算a+b后比较各集合的代表元形式可得.
【解析】由题意设a=2k,b=2m+1,其中k,m都是整数,
则a+b=2k+2m+1=2(k+m)+1,其中k+m是整数,可以是奇数也可以是偶数,
∴a+b∈B,
故选:B.
3.[多选](2022·贵州·贵阳一中高一阶段练习)在整数集Z中,被5除所得余数为k的所有整数组成一个“类”,记为[k],即[k]={5n+k|n∈Z},k=0,1,2,3,4. 下列结论正确的是( )
A.2 022∈[2]
B.-3∈[3]
C.Z=0∪1∪2∪3∪4
D.整数a,b属于同一个“类”的充要条件是a−b∈[0]
【答案】ACD
【分析】根据“类”的定义对选项进行分析,从而确定正确答案.
【解析】2022=404×5+2,所以2022∈2,A选项正确.
−3=−5+2,所以−3∈2,B选项错误.
整数是由5的倍数、5的倍数加1、5的倍数加2、5的倍数加3、5的倍数加4所构成,
所以Z=0∪1∪2∪3∪4,C选项正确.
当a,b属于同一个“类”时,设a=5n1+k,b=5n2+k,n1,n2∈Z,k=0,1,2,3,4,
所以a−b=5n1−n2∈0;
当a−b∈[0]时,a−b=5n,n∈Z,所以a=5n+b,a=5n+b=b,
即a被5除所得余数和b被5除所得余数相等,也即a,b属于同一个“类”.
综上所述,整数a,b属于同一个“类”的充要条件是a−b∈[0],D选项正确.
故选:ACD
4.(2022·海南华侨中学高一期中)设集合A=−1,0,1,集合B=x∈N|6x+1∈N
(1)用列举法写出集合B
(2)定义:A∗B=x,yx∈A∩B,y∈A∪B,求A∗B中元素的个数.
【答案】(1)B=0,1,2,5 (2)10
【分析】(1)由x∈N,6x+1∈N,解得x;
(2)先求出A∩B=0,1,A∪B=−1,0,1,2,5,根据定义求出A∗B,继而得解.
【解析】(1)由x∈N,6x+1∈N,所以x可以取0,1,2,5,所以B=0,1,2,5.
(2)由题意可知:B=0,1,2,5.
∴A∩B=0,1,A∪B=−1,0,1,2,5
∵A∗B=(x,y)x∈A∩B,y∈A∪B
∴A∗B=(0,−1),0,0,0,1,0,2,0,5,1,−1,1,0,1,1,1,2,1,5.
∴A∗B中元素的个数为10.
必会题型二:集合间的基本关系
1.(2022·上海市彭浦中学高一期中)下列表示错误的是( )
A.0∉∅ B.∅⊆1,2
C.x,y2x+y=103x−y=5=3,4 D.若A⊆B,则A∪B=B
【答案】C
【分析】由元素与集合的关系可判断A;由集合与集合的包含关系可判断B;由描述法可判断C;由集合的包含关系与并集的定义可判断D
【解析】对于A:因为空集没有任何元素,故0∉∅,故A正确;
对于B:因为空集是任何集合的子集,故∅⊆1,2,故B正确;
对于C:x,y2x+y=103x−y=5表示2x+y=10与3x−y=5的交点所构成的集合,
所以x,y2x+y=103x−y=5=3,4,故C错误;
对于D:若A⊆B,则A∪B=B,故D正确;
故选:C
2.[多选]已知集合A=0,a+b,ab,A=2,2-b,c若A=B,则a+b+c的值可能为( )
A.32 B.2 C.232 D.12
【答案】ABD
【分析】根据A=B,得到2-b=0或c=0,分类讨论得到a的值,根据元素的互异性,舍去不合要求的解,求出a+b+c的值.
【解析】因为A=B,所以2-b=0或c=0.
①当b=2时,A=0,a+2,a2,B=2,0,c,
所以a+2=2或a2=2,得a=0或4.
当a=0时,A=0,2不合题设,舍去.
当a=4时,A=0,6,2,c=6,此时a+b+c=12.
②当c=0时,A=0,a+b,ab,B=2,2-b,0,
所以a+b=2ab=2-b或a+b=2-bab=2,解得:a=0b=2或a=1b=1或a=1b=12
当a=0时,A=0,2不合题设,舍去.
当a=1b=1时,A=B=0,2,1,此时a+b+c=2.
当a=1b=12时,A=B=0,32,2,此时a+b+c=32.
故选:ABD
3.已知集合A满足1,2⊆A⊆1,2,3,4,5,2,3⊆A⊆1,2,3,5,6,则满足条件的集合A的个数为( )
A.8个 B.4个 C.2个 D.1个
【答案】C
【分析】根据给定的条件,确定集合A中元素即可求解作答.
【解析】因1,2⊆A⊆1,2,3,4,5,2,3⊆A⊆1,2,3,5,6,则有1,2,3都是集合A中元素,4,6都不在A中,5可以在A中,
因此集合A可以是{1,2,3}或{1,2,3,5},
所以满足条件的集合A的个数为2.
故选:C
4.(2022·上海·华师大二附中高一期中)已知集合A=xax2+3x−2=0有且仅有两个子集,则满足条件的实数a组成的集合是___________
【答案】−98,0
【分析】根据集合A的子集的个数得到集合A中只有一个元素,然后分a=0和a≠0两种情况求解即可.
【解析】因为集合A有且仅有两个子集,所以集合A中只有一个元素,即方程ax2+3x−2=0只有一个解,
当a=0时,3x−2=0,只有一个解,满足要求;
当a≠0时,Δ=9+8a=0,解得a=−98,所以a=−98或0.
故答案为:−98,0.
必会题型三:集合的基本运算
1.(广东省深圳科学高中2022-2023学年高一上学期期中数学试题)若全集U={1,2,3,4,5,6,7,8,9},A={1,2,3,5},B={1,2,4,6,7,8},则∁UA∪∁UB=( )
A.∅ B.{3,4,5,6,7,8,9} C.{9} D.{1,2}
【答案】B
【分析】由补集与并集的概念求解,
【解析】由题意得∁UA={4,6,7,8,9},∁UB={3,5,9},∁UA∪∁UB={3,4,5,6,7,8,9}
故选:B
2.(2022·陕西·渭南市瑞泉中学高一阶段练习)已知集合M=x−1
【答案】A
【分析】由定义域得到不等式,解不等式求出N=−1,32,从而求出交集.
【解析】3+x−2x2≥0,解得:−1≤x≤32,所以N=−1,32,
所以M∩N=−1,1∩−1,32=−1,1.
故选:A
3.[多选](辽宁省名校联盟2022-2023学年高一11月选科适应性考试数学试题)对于集合M,N,定义M−N={xx∈M且x∉N},设全集U=x∈Z−3
C.M−N={−2} D.∁U(N−M)={−2,−1,2,3}
【答案】CD
【分析】根据集合的新定义以及交并补运算,即可求解.
【解析】根据集合的互异性,即可判断A错,
M的非空真子集个数为23−2=6,即可判断B错,
根据M−N={xx∈M且x∉N},即可判断C对,
N−M={0,1},∁U(N−M)={−2,−1,2,3},即可判断D对,
故选:CD.
4.(湖南省衡阳市田家炳实验中学2022-2023学年高一上学期期中数学试题)已知集合A=x3
(2)求:∁RA∪B,A∪(∁RB).
【答案】(1)xx<2或x>10,xx≤3或x≥5;
(2)R,xx<2或3
【分析】根据集合的交、并、补运算求解即可.
【解析】(1)由题意,A∪B={x|2≤x≤10},A∩B={x|3
(2)由题意,∁RA =xx≤3或x≥5,∁RB= xx<2或x>10,
故∁RA∪B=R,A∪(∁RB)= xx<2或3
5.(浙江省台州市三门第二高级中学2022-2023学年高一上学期第一次月考数学试题)已知集合A=xa−1
(2)若A∩B=A,求实数a的取值范围.
【答案】(1)A∪B=x−2≤x<7,∁RA∩B=x−2≤x≤1
(2)a≤−4或−1≤a≤12
【分析】(1)代入a=2,得到集合A,根据集合运算的概念求解即可;
(2)由已知可得,A⊆B,对A=∅与A≠∅分别求解.
【解析】(1)当a=2时,集合A=x1
又U=R,∴∁RA=x|x≤1或x≥7,
∴∁RA∩B=x−2≤x≤1.
(2)若A∩B=A,则A⊆B,
当a−1≥2a+3,即a≤−4时,A=∅,满足题意;
当A≠∅,即a>−4时,应满足a−1≥−22a+3≤4,解得−1≤a≤12;
综上知,实数a的取值范围是a≤−4或−1≤a≤12.
必会题型四:Venn图法解决集合运算问题
1.(2022·陕西·交大附中高一期中)已知集合A=x∈N1≤x≤6,B=xx2−x−6≤0,则如图中阴影部分表示的集合为( ).
A.0,1,2 B.1,2,3 C.−3,0,1,2 D.−2,0,1,2,3
【答案】B
【分析】由自然数集N的定义化简集合A,解二次不等式化简集合B,由韦恩图可知阴影部分表示的集合为A∩B,由此得解.
【解析】易知A=x∈N1≤x≤6=1,2,3,4,5,6,
由x2−x−6≤0得x−3x+2≤0,故−2≤x≤3,则B=x−2≤x≤3,
由韦恩图可知阴影部分表示的集合为A∩B,而A∩B=1,2,3,
所以图中阴影部分表示的集合为1,2,3.
故选:B.
2.(重庆市璧山区2022-2023学年高一上学期10调研数学试题)图中阴影部分表示的集合为( )
A.∁UA∩B B.A∩∁UB C.∁UA∩∁UB D.∁U(A∩B)
【答案】A
【分析】根据集合的交并补运算逐个选项验证即可.
【解析】根据补集和交集的概念可知A选项的∁UA∩B符合题意;
由图可知,阴影部分为集合B的子集,而∁UB不是B的子集,故排除选项B、C;
∁U(A∩B)表示的区域如图:
所以D不符题意;
故选:A.
3.[多选](江苏省苏州市第五中学2022-2023学年高一上学期10月阶段性测试数学试题)正确表示图中阴影部分的是( )
A.∁UM∩∁UN B.∁UM∪N
C.∁UM∩N D.∁UM∪N
【答案】AD
【分析】根据阴影位于M与N并集的外部即可作出判断.
【解析】根据图中阴影可知,∁UM∪N符合题意,
又∁UM∪N=∁UM∩∁UN.
故选:AD
4.某年级举行数学、物理、化学三项竞赛,共有80名学生参赛,其中参加数学竞赛有40人,参加物理竞赛有45人,参加化学竞赛有30人,同时参加物理、化学竞赛有15人,同时参加数学、物理竞赛有20人,同时参加数学、化学竞赛有10人,这个年级三个学科竞赛都参加的学生共有______名.
【答案】10
【分析】利用容斥原理即可求解.
【解析】设三个学科竞赛都参加的学生为x人,
结合已知条件可知,
只参加物理、化学两个科目竞赛的学生为15−x人,
只参加数学、物理两个科目竞赛的学生为20−x人,
只参加数学、化学两个科目竞赛的学生为10−x人,
只参加物理竞赛的学生为45−(15−x)−x−(20−x)=10+x人,
只参加化学竞赛的学生为30−(15−x)−x−(10−x)=5+x人,
只参加数学竞赛的学生为40−(20−x)−x−(10−x)=10+x人,
如下图所示:
故45−20−15−x+40−20−10−x+30+20−x=80,解得x=10,
故都参加的学生人数为10人,
故答案为:10.
必会题型五:分类讨论法解决元素与集合关系问题
1.(北京市第十五中学南口学校2022-2023学年高一上学期期中考试数学试题)已知M=1,2,a2−3a−1,N=1,3,且N⫋M,则a的值为( )
A.−1 B.4
C.−1或4 D.1或−4
【答案】C
【分析】根据集合间的关系和元素与集合的关系,可知a2−3a−1=3,解方程即可得出答案.
【解析】因为M=1,2,a2−3a−1,N=1,3,且N⫋M,
所以a2−3a−1=3,解得:a=−1或a=4,
故选:C.
2.[多选](四川省成都市树德中学2022-2023学年高一上学期10月月考数学试题)下列四个命题:其中不正确的命题为( )
A.已知集合A=yy=x2+1,集合B=xy=x2+1,则A∩B=∅
B.集合x∈N|5x+1∈N中有两个元素
C.由方程x2−2x+1=0的所有实根构成的集合中的元素之和为2
D.记A=x|x=2k+1,k∈Z,B=x|x=4n±1,n∈Z,则A=B
【答案】AC
【分析】利用集合的定义可判断对错.
【解析】A=y|y≥1,B=R,A∩B=x|x≥1,所以A选项错误;
因为集合x∈N|5x+1∈N=0,4,所以B选项正确;
由于x|x2−2x+1=0=1,集合中只有一个元素,和为1,所以C选项错误;
对于集合A,当k=2n时,x=4n+1,n∈Z,当k=2n−1时,x=4n−1,n∈Z,即A=x|x=4n±1,n∈Z=B,所以D选项正确.
故选:AC.
3.(河南省南阳市六校2022-2023学年高一上学期期中考试数学试题)已知集合A=1,2,3,B=1,m,n,若2−m∈A,n+2∈A,则m+n=______.
【答案】−1
【分析】首先利用集合与元素的关系和集合元素的特征得到m=0n=−1或m=−1n=0,即可得到答案.
【解析】因为2−m∈A,所以2−m=1或2−m=2或2−m=3,
解得m=1或m=0或m=−1,
因为n+2∈A,所以n+2=1或n+2=2或n+2=3,
解得n=−1或n=0或n=1,
又因为B={1,m,n},所以m=0n=−1或m=−1n=0,即m+n=−1.
故答案为:−1
4.(1)设集合A={a2,a+1,−1},B={2a-1,|a-2|,3a2+4},A∩B=−1,求实数a的值.
(2)设集合A=x2,2x−1,−4,B=x−5,1−x,9,若A∩B=9,求实数x的值.
【答案】(1)a=0;(2)x=−3
【分析】根据A∩B的结果,对A、B的元素分类讨论即可
【解析】(1)∵A∩B=−1,∴−1∈B,而|a-2|≥0,3a2+4>0,∴2a-1=-1,则a=0,
此时A={0,1,-1},B={-1,2,4},A∩B=−1,符合题意.
故a=0;
(2)因为A=x2,2x−1,−4,B=x−5,1−x,9,A∩B=9,
若x2=9,则x=±3,
当x=3时,x−5=1−x=−2,不满足题意;
当x=−3时,A={9,−7,−4},B={−8,4,9},A∩B=9,满足题意;
若2x−1=9,则x=5,此时A=25,9,−4,B=0,−4,9,则A∩B={9,−4},不满足题意;
综上,x=−3.
必会题型六:根据集合包含关系求参数值或范围
1. (山东省菏泽市2022-2023学年高一上学期期中数学试题)设集合A=x−1≤x≤4,集合B=xx≥a,若A⊆B,则a的取值范围为( )
A.a≥4 B.−1≤a≤4
C.a<−1 D.a≤−1
【答案】D
【分析】根据集合的包含关系即可得解.
【解析】因为集合A=x−1≤x≤4,集合B=xx≥a,A⊆B,
所以a≤−1.
故选:D.
2.(辽宁省朝阳市建平县实验中学2022-2023学年高一上学期第一次月考数学试题)集合A=xx<−1或x≥3,B=xax+1≤0若B⊆A,则实数a的取值范围是( )
A.−13,1 B.−13,1
C.−∞,1∪0,+∞ D.−13,0∪0,1
【答案】A
【分析】根据B⊆A,分B=∅和B≠∅两种情况讨论,建立不等关系即可求实数a的取值范围.
【解析】∵B⊆A,
∴①当B=∅时,即ax+1≤0无解,此时a=0,满足题意.
②当B≠∅时,即ax+1≤0有解,
当a>0时,可得x≤−1a,
要使B⊆A,则需要a>0−1a<−1,解得0
要使B⊆A,则需要a<0−1a≥3,解得−13≤a<0,
综上,实数a的取值范围是−13,1.
故选:A.
3.(辽宁省朝阳市建平县实验中学2022-2023学年高一上学期第一次月考数学试题)已知集合A=x2a+1≤x≤3a−5,B={xx<−1或x>16} .
(1)若A为非空集合,求实数a的取值范围;
(2)若A∩B=A,求实数a的取值范围.
【答案】(1)a≥6
(2)a<6或a>152
【分析】(1)由条件可知,2a+1≤3a−5,即可求解不等式;
(2)分A=∅和A≠∅两种情况,列不等式求解.
【解析】(1)若A为非空集,则2a+1≤3a−5,解得:a≥6;
(2)若A∩B=A,则A⊆B,
当A=∅时,2a+1>3a−5,解得:a<6,
当A≠∅时,2a+1≤3a−53a−5<−1 ,解得:∅
或2a+1≤3a−52a+1>16,解得:a>152
所以实数a的取值范围是a<6或a>152
4.(山东省青岛市青岛第二中学2022-2023学年高一上学期期中数学试题)已知集合.A=x|a−2≤x≤a+2,B={x|x≤−1或x≥2}.
(1)当a=3时,求A∩B,A∪∁RB;
(2)若A∪B=R,求实数a的取值范围
【答案】(1)A∩B={x|2≤x≤5},A∪∁RB= {x−1
【分析】(1)应用集合的交、并、补运算求集合即可;
(2)根据并集结果得a−2≤−1a+2≥2,即可求参数范围.
【解析】(1)a=3时,A={x|1≤x≤5},所以A∩B={x|2≤x≤5},
因为∁RB= x−1
5.(江苏省苏州市吴县中学教育集团2022-2023学年高一上学期10月学业质量阳光指标调研数学试题)设全集为U=R,集合A={x|−2
(1)求如图阴影部分表示的集合;
(2)已知集合C={x|a
【答案】(1)x|−2
(2)依题意可得a>02a≤6,解得即可.
【解析】(1)解:因为A={x|−2
所以图中阴影部分表示∁AA∩B=x|−2
所以a>02a≤6,解得0
(1)若a=−1,求A∪∁RB;
(2)若A∩B=∅,求a的取值范围.
【答案】(1)A∪CRB=x−2≤x≤5
(2)x−12≤a≤2或a>3
【分析】(1)根据题意,先求出集合A的补集,再利用集合的并集运算求解即可;
(2)根据集合的包含关系分A=∅和A≠∅两种情况进行讨论即可求解.
【解析】(1)若a=−1,则集合A=x−2≤x≤2,
所以∁RB=x−1≤x≤5,
所以A∪CRB=x−2≤x≤5;
(2)因为集合A=x2a≤x≤a+3,B={x|x<−1或x>5},
因为A∩B=∅,所以分以下两种情况:
若A=∅,即2a>a+3,解得a>3,满足题意,
若A≠∅,则2a≥−1a+3≤52a≤a+3
解得−12≤a≤2,
综上所述a的取值范围为x−12≤a≤2或a>3
7.已知A=xx2−2x−3≤0,B=xx−a≤1,a∈R.
(1)若A∪B=A,求出实数a的取值范围;
(2)若a∈A,求A∩B.
【答案】(1)0≤a≤2
(2)答案见解析
【分析】(1)求出集合AB,然后根据并集结果列不等式求解即可;
(2)分a−1<−1
B=xx−a≤1,a∈R=−1+a,1+a
∵A∪B=A,∴B⊆A∴−1+a≥−11+a≤3
解得0≤a≤2
(2)由(1)A=−1,3,B=−1+a,1+a,a∈−1,3,
当a−1<−1
(1)若a=1,求A∪B;
(2)求实数a的取值范围,使___________成立.
从①A⊆∁RB,②B⊆∁RA,③∁RA∩B=∅中选择一个填入横线处求解.
注:如果选择多个条件分别解答,按第一个解答计分.
【答案】(1)x0
选2,a≤0或a≥6;
选3,2≤a≤4.
【分析】(1)根据对数函数的单调性求出集合A,根据一元二次不等式的解法求出集合B,结合并集的概念和运算即可得出结果;
(1)根据(1)和补集的概念和运算求出∁RA和∁RB,利用集合间的包含关系和交并补的运算即可求出对应条件的参数.
【解析】(1)A={xlog2(x−1)<2}={x0
若选①,A⊆∁RB,则a+1≤1或a−1≥5,
解得a≤0或a≥6,所以a的取值范围为a≤0或a≥6;
若选②,B⊆∁RA,则a+1≤1或a−1≥5,
解得a≤0或a≥6,所以a的取值范围为a≤0或a≥6;
若选③,(∁RA)∩B=∅,则1≤a−1a+1≤5,
解得2≤a≤4,所以a的取值范围为2≤a≤4.
相关资料
更多









