苏科版九年级下册第6章 图形的相似6.7用相似三角形解决问题导学案及答案

这是一份苏科版九年级下册第6章 图形的相似6.7用相似三角形解决问题导学案及答案，共4页。学案主要包含了学习目标，知识回顾，例题分析，课堂小结，强化检测，拓展延伸等内容，欢迎下载使用。

【学习目标】
能理解折叠的本质并能运用其解题
提高动手能力和空间想象能力
激发学习兴趣，培养乐于动手、勤于实践的意识，提高综合解题能力。
【知识回顾】
1、课前小测
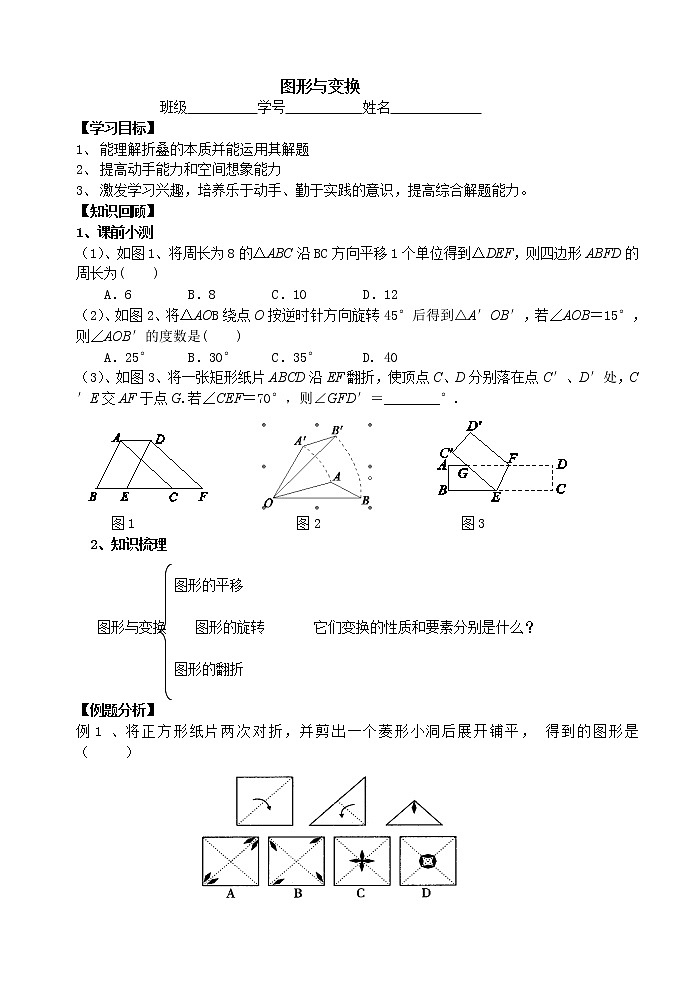
（1）、如图1、将周长为8的△ABC沿BC方向平移1个单位得到△DEF，则四边形ABFD的周长为( )
A．6 B．8 C．10 D．12
（2）、如图2、将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′，若∠AOB＝15°，则∠AOB′的度数是( )
A．25° B．30° C．35° D. 40
（3）、如图3、将一张矩形纸片ABCD沿EF翻折，使顶点C、D分别落在点C′、D′处，C′E交AF于点G.若∠CEF＝70°，则∠GFD′＝________°.
图1 图2 图3
2、知识梳理
图形的平移
图形与变换 图形的旋转 它们变换的性质和要素分别是什么？
图形的翻折
【例题分析】
例1 、将正方形纸片两次对折，并剪出一个菱形小洞后展开铺平，得到的图形是（ ）

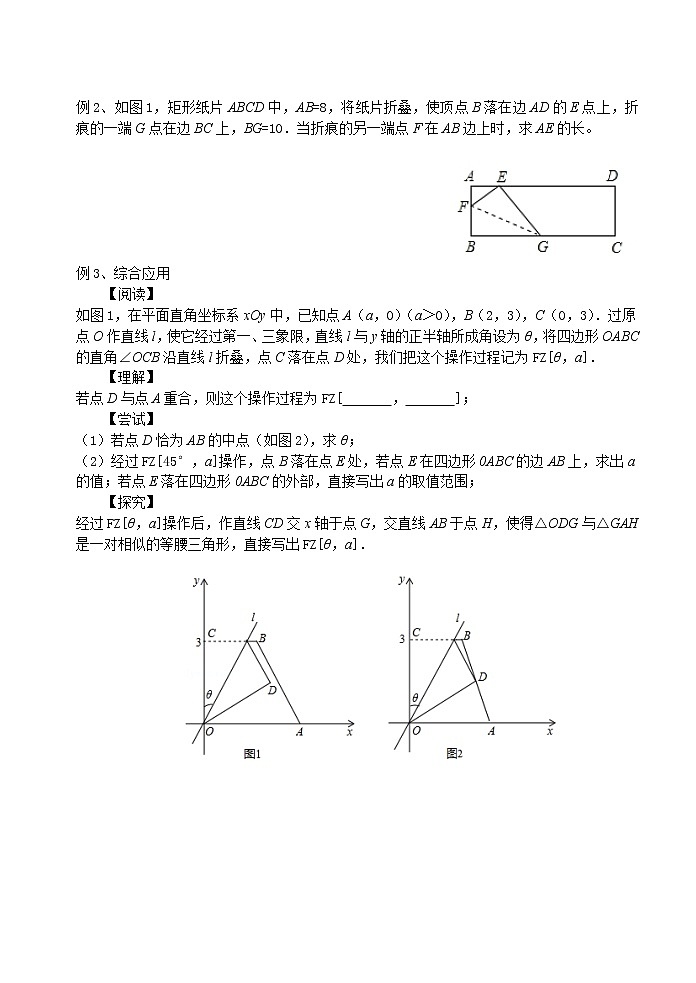
例2、如图1，矩形纸片ABCD中，AB=8，将纸片折叠，使顶点B落在边AD的E点上，折痕的一端G点在边BC上，BG=10．当折痕的另一端点F在AB边上时，求AE的长。
例3、综合应用
【阅读】
如图1，在平面直角坐标系xOy中，已知点A（a，0）（a＞0），B（2，3），C（0，3）．过原点O作直线l，使它经过第一、三象限，直线l与y轴的正半轴所成角设为θ，将四边形OABC的直角∠OCB沿直线l折叠，点C落在点D处，我们把这个操作过程记为FZ[θ，a]．
【理解】
若点D与点A重合，则这个操作过程为FZ[ ， ]；
【尝试】
（1）若点D恰为AB的中点（如图2），求θ；
（2）经过FZ[45°，a]操作，点B落在点E处，若点E在四边形0ABC的边AB上，求出a的值；若点E落在四边形0ABC的外部，直接写出a的取值范围；
【探究】
经过FZ[θ，a]操作后，作直线CD交x轴于点G，交直线AB于点H，使得△ODG与△GAH是一对相似的等腰三角形，直接写出FZ[θ，a]．
【课堂小结】
【强化检测】
A
B
C
D
B’
1
C’
D’
1、如图，把一个长方形的纸片对折两次，然后剪下一个角，为了得到一个钝角为120° 的菱形，剪口与第二次折痕所成角的度数应为（ ）

A．15°或30° B．30°或45° C．45°或60° D．30°或60°
2、如图，将矩形ABCD绕点A顺时针旋转到矩形A’B’C’D’的位置， 旋转角为 (0<<90)。若1=110，则= 。
3、如图a是长方形纸带，∠DEF=20°将纸带沿EF 折叠成图b，再沿BF 折叠成图c，则图c中的∠CFE 的度数是 ．
A
D
C
B
E
C
B
F
D
C
D
E
F
G
A
B
E
F
G
A
图a
图b
图c
【拓展延伸】
1、折叠矩形纸片ABCD，使点B落在AD上的一点E处，折痕的两端点分别在AB、BC上（含端点），且AB=6，BC=10.设AE=x,则x 的取值范围是 ．
A
B
C
D
A
B
C
E
F
B′
2、将三角形纸片（△ABC）按如图所示的方式折叠，使点B落在边AC上，记为点B′，折痕为EF。已知AB=AC=3，BC=4,若以点B′、F、C为顶点的三角形与△ABC相似，求BF的长。
3、已知一个矩形纸片OACB，将该纸片放置在平面直角坐标洗中，点A（11，0），点B（0，6），点P为BC边上的动点（点P不与点B、C重合），经过点O、P折叠该纸片，得点B′和折痕OP．设BP=t．
（Ⅰ）如图①，当∠BOP=30°时，求点P的坐标；
（Ⅱ）如图②，经过点P再次折叠纸片，使点C落在直线PB′上，得点C′和折痕PQ，若AQ=m，试用含有t的式子表示m；
（Ⅲ）在（Ⅱ）的条件下，当点C′恰好落在边OA上时，求点P的坐标（直接写出结果即可）．