2022-2023学年上学期八年级数学期末模拟测试卷（12）

这是一份2022-2023学年上学期八年级数学期末模拟测试卷（12），共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022-2023学年上学期八年级数学期末模拟测试卷（12）
一、选择题（本大题共8小题，每小题3分，共24分。在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上）
1．的平方根是（　　）
A． B．±6 C． D．﹣6
2．下列图形都是由两个全等三角形组合而成，其中是轴对称图形的是（　　）
A． B．
C． D．
3．在平面直角坐标系中，点P（﹣3，1）关于y轴对称点在（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
4．下列生活中的一些事实运用了“三角形稳定性”的是（　　）
A． B．
C． D．
5．某市城市轨道交通6号线工程的中标价格是81750000元，81750000精确到100000，用科学记数法可表示为（　　）
A．8.17×107 B．8.17×108 C．8.18×107 D．8.18×108
6．如图，在△ABC中，AB＝AC＝8cm，D是BC上的一点，DE⊥AB于点E，DF⊥AC于点F，已知DE+DF＝6cm，则△ABC的面积是（　　）

A．12cm2 B．48cm2 C．24cm2 D．64cm2
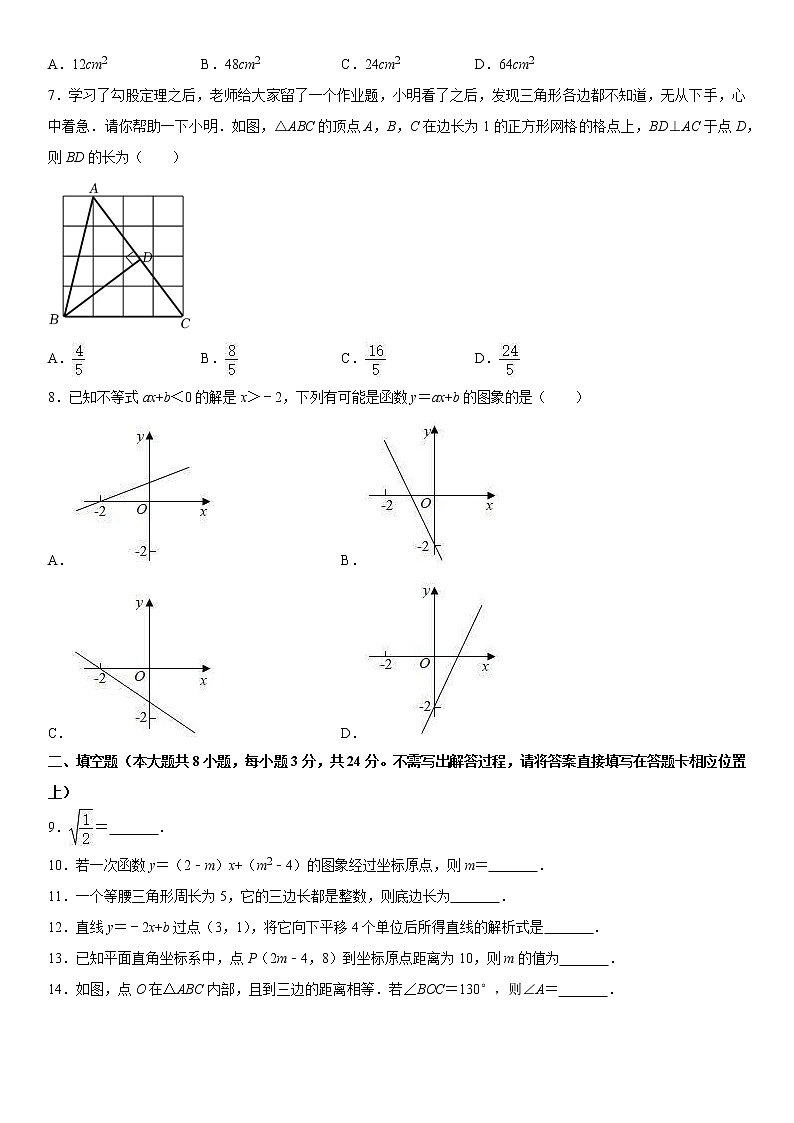
7．学习了勾股定理之后，老师给大家留了一个作业题，小明看了之后，发现三角形各边都不知道，无从下手，心中着急．请你帮助一下小明．如图，△ABC的顶点A，B，C在边长为1的正方形网格的格点上，BD⊥AC于点D，则BD的长为（　　）

A． B． C． D．
8．已知不等式ax+b＜0的解是x＞﹣2，下列有可能是函数y＝ax+b的图象的是（　　）
A． B．
C． D．
二、填空题（本大题共8小题，每小题3分，共24分。不需写出解答过程，请将答案直接填写在答题卡相应位置上）
9．＝　 　．
10．若一次函数y＝（2﹣m）x+（m2﹣4）的图象经过坐标原点，则m＝　 　．
11．一个等腰三角形周长为5，它的三边长都是整数，则底边长为　 　．
12．直线y＝﹣2x+b过点（3，1），将它向下平移4个单位后所得直线的解析式是　 　．
13．已知平面直角坐标系中，点P（2m﹣4，8）到坐标原点距离为10，则m的值为　 　．
14．如图，点O在△ABC内部，且到三边的距离相等．若∠BOC＝130°，则∠A＝　 　．

15．已知点B（3，1）和直线l：y＝﹣x+2，A是直线l上一点，连接AB，以A为直角顶点作等腰直角三角形ABC，使点C落在第一象限，当AC最短时，点C的坐标是 　 　．
16．如图，在四边形ABCD中，∠A+∠C＝180°，E、F分别在BC、CD上，且AB＝BE，AD＝DF，M为EF的中点，DM＝3，BM＝4，则五边形ABEFD的面积是　 　．

三、解答题（本大题共9小题，共72分。请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
17．（6分）计算：
（1）﹣（+1）0+（﹣2）﹣2；
（2）求（x+1）3﹣64＝0中x的值．






18．（6分）如图，△ABC在平面直角坐标系中三个顶点的坐标分别是A（3，4），B（1，2），C（5，1）．
（1）画出△ABC关于x轴对称图形△DEF．
（2）分别写出D、E、F三点的坐标．
（3）若P（a，b），请表示其向下平移两个单位后关于y轴对应点Q的坐标（用含a，b的式子表示）．





19．（6分）如图，已知△ABC中，∠ACB＝90°，AC＝BC，D为AC上一点，延长BC到E，使得CE＝CD．
求证：BD⊥AE．







20．（6分）平面直角坐标系中，直线y＝x﹣1的图象如图所示，它与直线y＝﹣2x+4的图象都经过A （2，0），且两直线与y轴分别交于B、C两点．
（1）直接画出一次函数y＝﹣2x+4的图象；
（2）直接写出B、C两点的坐标；
（3）判断△ABC的形状，并说明理由．








21．（8分）如图，AD为△ABC的角平分线，DE⊥AB于点E，DF⊥AC于点F，连接EF交AD于点O，∠BAC＝60°．
探究：判断△AEF的形状，并说明理由；
发现：DO与AD之间有怎样的数量关系，请直接写出你的结论，不必说明理由．









22．（8分）某地发生强烈地震，在抗震救灾中得知，甲、乙两个重灾区急需一种大型挖掘机，甲地需要25台，乙地需要23台；A、B两省获知情况后慷慨相助，分别捐赠该型号挖掘机26台和22台并将其全部调往灾区．如果从A省调运一台挖掘机到甲地要耗资0.4万元，到乙地要耗资0.3万元；从B省调运一台挖掘机到甲地要耗资0.5万元，到乙地要耗资0.2万元．设从A省调往甲地x台挖掘机，A、B两省将捐赠的挖掘机全部调往灾区共耗资y万元．
（1）请直接写出y与x之间的函数关系式及自变量x的取值范围；
（2）若要使总耗资不超过15万元，有哪几种调运方案？
（3）怎样设计调运方案能使总耗资最少？最少耗资是多少万元？





23．（10分）如图，△ABC中，AD是边BC上的高，CF是边AB上的中线，且DC＝BF，DE⊥CF于点E．
（1）求证：E是CF的中点．
（2）若∠B＝30°，求∠BCF的度数．







24．（10分）甲、乙两地间的直线公路长为400千米．一辆轿车和一辆货车分别沿该公路从甲、乙两地以各自的速度匀速相向而行，货车比轿车早出发1小时，途中轿车出现了故障，停下维修，货车仍继续行驶．1小时后轿车故障被排除，此时接到通知，轿车立刻掉头按原路原速返回甲地（接到通知及掉头时间不计）．最后两车同时到达甲地，已知两车距各自出发地的距离y（千米）与轿车所用的时间x（小时）的关系如图所示，请结合图象解答下列问题：
（1）货车的速度是 　 　千米/小时；轿车的速度是 　 　千米/小时；t值为 　 　．
（2）求轿车距其出发地的距离y（千米）与所用时间x（小时）之间的函数关系式并写出自变量x的取值范围；
（3）请直接写出货车出发多长时间两车相距90千米．




25．（12分）如图，△ABC中，∠ACB＝90°，AB＝10，BC＝6，若点P从点A出发，以每秒1个单位长度的速度沿折线A﹣C﹣B﹣A运动，设运动时间为t秒（t＞0）．

（1）若点P在AC上，且满足PA＝PB时，求此时t的值；
（2）若点P恰好在∠BAC的平分线上，求t的值．

答案与解析
一、选择题（本大题共8小题，每小题3分，共24分。在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上）
1．的平方根是（　　）
A． B．±6 C． D．﹣6
解：＝6，6的平方根是±．
答案：A．
2．下列图形都是由两个全等三角形组合而成，其中是轴对称图形的是（　　）
A． B．
C． D．
解：A、不是轴对称图形，故此选项错误；
B、是轴对称图形，故此选项正确；
C、不是轴对称图形，故此选项错误；
D、不是轴对称图形，故此选项错误；
答案：B．
3．在平面直角坐标系中，点P（﹣3，1）关于y轴对称点在（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
解：点P（﹣3，1）关于y轴对称点坐标为：（3，1），
则（3，1）在第一象限．
答案：A．
4．下列生活中的一些事实运用了“三角形稳定性”的是（　　）
A． B．
C． D．
解：儿童座架利用三角形的稳定性，座架形成三角形不变形，结实，故C符合题意；
A、B、D不是三角形，故选项不符合题意．
答案：C．
5．某市城市轨道交通6号线工程的中标价格是81750000元，81750000精确到100000，用科学记数法可表示为（　　）
A．8.17×107 B．8.17×108 C．8.18×107 D．8.18×108
解：81750000精确到100000，用科学记数法可表示为8.18×107．
答案：C．
6．如图，在△ABC中，AB＝AC＝8cm，D是BC上的一点，DE⊥AB于点E，DF⊥AC于点F，已知DE+DF＝6cm，则△ABC的面积是（　　）

A．12cm2 B．48cm2 C．24cm2 D．64cm2
解：如图，连接AD，

∵S△ABC＝S△ABD+S△ACD，
∴S△ABC＝×8×（DE+DF）＝24cm2，
答案：C．
7．学习了勾股定理之后，老师给大家留了一个作业题，小明看了之后，发现三角形各边都不知道，无从下手，心中着急．请你帮助一下小明．如图，△ABC的顶点A，B，C在边长为1的正方形网格的格点上，BD⊥AC于点D，则BD的长为（　　）

A． B． C． D．
解：由勾股定理得：AC＝＝5，
∵BD⊥AC，
∴△ABC的面积＝AC×BD＝×4×4，
∴BD＝，
答案：C．
8．已知不等式ax+b＜0的解是x＞﹣2，下列有可能是函数y＝ax+b的图象的是（　　）
A． B．
C． D．
解：∵不等式ax+b＜0的解是x＞﹣2，
∴直线y＝ax+b与x轴交点为（﹣2，0）且y随x增大而减小，
答案：C．
二、填空题（本大题共8小题，每小题3分，共24分。不需写出解答过程，请将答案直接填写在答题卡相应位置上）
9．＝　　．
解：＝＝＝．
答案：．
10．若一次函数y＝（2﹣m）x+（m2﹣4）的图象经过坐标原点，则m＝　﹣2　．
解：∵一次函数y＝（2﹣m）x+（m2﹣4）的图象经过坐标原点，
∴，解得m＝﹣2．
答案：﹣2．
11．一个等腰三角形周长为5，它的三边长都是整数，则底边长为　1　．
解：若底边为1，则腰为2，符合三角形的构成条件；
若底边为2，则腰为1.5，不符合条件则舍去；
若底边为3，则腰为1，不能构成三角形，舍去．
答案：1．
12．直线y＝﹣2x+b过点（3，1），将它向下平移4个单位后所得直线的解析式是　y＝﹣2x+3　．
解：将（3，1）代入y＝﹣2x+b，
得：1＝﹣6+b，
解得：b＝7，
∴y＝﹣2x+7，
将直线y＝﹣2x+7向下平移4个单位后所得直线的解析式是y＝﹣2x+7﹣4，即y＝﹣2x+3，
答案：y＝﹣2x+3．
13．已知平面直角坐标系中，点P（2m﹣4，8）到坐标原点距离为10，则m的值为　5或﹣1　．
解：由题意得：
（2m﹣4）2+82＝102，
解得：m＝5或﹣1．
答案：5或﹣1．
14．如图，点O在△ABC内部，且到三边的距离相等．若∠BOC＝130°，则∠A＝　80°　．

解：∵点O到△ABC三边的距离相等，
∴BO平分∠ABC，CO平分∠ACB，
∴∠A＝180°﹣（∠ABC+∠ACB）
＝180°﹣2（∠OBC+∠OCB）
＝180°﹣2×（180°﹣∠BOC）
＝180°﹣2×（180°﹣130°）
＝80°，
答案：80°．
15．已知点B（3，1）和直线l：y＝﹣x+2，A是直线l上一点，连接AB，以A为直角顶点作等腰直角三角形ABC，使点C落在第一象限，当AC最短时，点C的坐标是 　（1，1）　．
解：∵三角形ABC为等腰直角三角形，∠BAC＝90°，
∴AC＝AB，
∴当AB最短时，AC最短，即AB⊥直线l，

设点A坐标为（m，﹣m+2），
∵B（3，1）
∴AB2＝（3﹣m）2+（1+m﹣2）2＝2m2﹣8m+10＝2（m﹣2）2+2，
∴m＝2时，点A坐标为（2，0），AB2＝2为最小值，
∴AB＝AC＝，
∴BC＝AB＝2，
∴点C横坐标为x＝3﹣2＝1，
把x＝1代入y＝﹣x+2得y＝1，
∴点C坐标为（1，1）．
答案：（1，1）．
16．如图，在四边形ABCD中，∠A+∠C＝180°，E、F分别在BC、CD上，且AB＝BE，AD＝DF，M为EF的中点，DM＝3，BM＝4，则五边形ABEFD的面积是　12　．

解：延长BM至G，使MG＝BM＝4，连接FG、DG，如图所示：

∵M为EF中点，
∴ME＝MF，
在△BME和△GMF中，
，
∴△BME≌△GMF（SAS），
∴FG＝BE，∠MBE＝∠MGF，S△BEM＝S△GFM，
∴FG∥BE，
∴∠C＝∠GFC，
∵∠A+∠C＝180°，∠DFG+∠GFC＝180°，
∴∠A＝∠DFG，
∵AB＝BE，
∴AB＝FG，
在△DAB和△DFG中，
，
∴△DAB≌△DFG（SAS），
∴DB＝DG，S△DAB＝S△DFG，
∵MG＝BM，
∴DM⊥BM，
∴五边形ABEFD的面积＝△DBG的面积＝×BG×DM＝×8×3＝12，
答案：12．
三、解答题（本大题共9小题，共72分。请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
17．（6分）计算：
（1）﹣（+1）0+（﹣2）﹣2；
（2）求（x+1）3﹣64＝0中x的值．
解：（1）原式＝|﹣3|﹣1+
＝3﹣1+
＝2；
（2）∵（x+1）3﹣64＝0，
∴（x+1）3＝64．
∴x+1是64的立方根．
∴x+1＝4．
∴x＝3．
18．（6分）如图，△ABC在平面直角坐标系中三个顶点的坐标分别是A（3，4），B（1，2），C（5，1）．
（1）画出△ABC关于x轴对称图形△DEF．
（2）分别写出D、E、F三点的坐标．
（3）若P（a，b），请表示其向下平移两个单位后关于y轴对应点Q的坐标（用含a，b的式子表示）．

解：（1）如图，△DEF即为所求；

（2）D（3，﹣4）E（1，﹣2）F（5，﹣1）；
（3）Q（﹣a，b﹣2）．
19．（6分）如图，已知△ABC中，∠ACB＝90°，AC＝BC，D为AC上一点，延长BC到E，使得CE＝CD．
求证：BD⊥AE．

证明：

延长BD交AE于M，
∵∠ACB＝90°，
∴∠ACE＝180°﹣∠ACB＝180°﹣90°＝90°，
∴∠DCB＝∠ACE，
在△ACE和△BCD中
∵，
∴△ACE≌△BCD（SAS），
∴∠DBC＝∠CAE，
∵∠ACB＝90°，
∴∠DBC+∠BDC＝90°，
∵∠ADM＝∠BDC，
∴∠CAE+∠ADM＝90°，
∴∠AMD＝180°﹣90°＝90°，
∴BM⊥AE，
即BD⊥AE
20．（6分）平面直角坐标系中，直线y＝x﹣1的图象如图所示，它与直线y＝﹣2x+4的图象都经过A （2，0），且两直线与y轴分别交于B、C两点．
（1）直接画出一次函数y＝﹣2x+4的图象；
（2）直接写出B、C两点的坐标；
（3）判断△ABC的形状，并说明理由．

解：（1）画出函数图象如图；
（2）B（0，﹣1），C（0，4）；
（3）△ABC是直角三角形，理由如下：
∵A（2，0），B（0，1），C（0，4），
∴AB2＝22+12＝5，AC2＝22+42＝20，BC2＝（4+1）2＝25，
∵AB2+AC2＝BC2，
∴△ABC是直角三角形．

21．（8分）如图，AD为△ABC的角平分线，DE⊥AB于点E，DF⊥AC于点F，连接EF交AD于点O，∠BAC＝60°．
探究：判断△AEF的形状，并说明理由；
发现：DO与AD之间有怎样的数量关系，请直接写出你的结论，不必说明理由．

解：如图所示：

探究：△AEF是等边三角形，
∵AD为△ABC的角平分线，DE⊥AB，DF⊥AC，
∴DE＝DF，∠AED＝∠AFD＝90°，
在Rt△AED和Rt△AFD中，

∴Rt△AED≌Rt△AFD（HL），
∴AE＝AF，
∵∠BAC＝60°，
∴△AEF是等边三角形
发现：DO＝AD，

∵Rt△AED≌Rt△AFD，
∴∠EAD＝∠CAD，
又∵∠BAC＝∠EAD+∠CAD＝60°，
∴∠EAD＝30°，
∴DE＝AD，
又∵DE⊥AB，
∴∠DEA＝90°，
又∵△AEF是等边三角形，
∴∠AEF＝60°，AD⊥EF，
又∵∠AED＝∠DEO+∠AEO，
∴∠DEO＝30°，
∴OD＝DE，
∴DO＝AD．
22．（8分）某地发生强烈地震，在抗震救灾中得知，甲、乙两个重灾区急需一种大型挖掘机，甲地需要25台，乙地需要23台；A、B两省获知情况后慷慨相助，分别捐赠该型号挖掘机26台和22台并将其全部调往灾区．如果从A省调运一台挖掘机到甲地要耗资0.4万元，到乙地要耗资0.3万元；从B省调运一台挖掘机到甲地要耗资0.5万元，到乙地要耗资0.2万元．设从A省调往甲地x台挖掘机，A、B两省将捐赠的挖掘机全部调往灾区共耗资y万元．
（1）请直接写出y与x之间的函数关系式及自变量x的取值范围；
（2）若要使总耗资不超过15万元，有哪几种调运方案？
（3）怎样设计调运方案能使总耗资最少？最少耗资是多少万元？

解：（1）由题意得：y＝0.4x+0.3（26﹣x）+0.5（25﹣x）+0.2（23﹣26+x），
或：y＝0.4x+0.3（26﹣x）+0.5（25﹣x）+0.2（22﹣25+x），
即：y＝﹣0.2x+19.7（3≤x≤25）；

（2）依题意，得﹣0.2x+19.7≤15，
解之，得，
又∵23.5≤x≤25，且x为整数，
∴x＝24或25，
即，要使总耗资不超过15万元，有如下两种调运方案：
方案一：从A省往甲地调运24台，往乙地调运2台；从B省往甲地调运1台，往乙地调运21台．
方案二：从A省往甲地调运25台，往乙地调运1台；从B省往甲地调运0台，往乙地调运22台．

（3）由（1）知：y＝﹣0.2x+19.7（3≤x≤25），
∵﹣0.2＜0，
∴y随x的增大而减小，
∴当x＝25时，y最小值＝﹣0.2×25+19.7＝14.7，
答：设计如下调运方案：从A省往甲地调运25台，往乙地调运1台；
从B省往甲地调运0台，往乙地调运22台，能使总耗资最少．
最少耗资为14.7万元．
23．（10分）如图，△ABC中，AD是边BC上的高，CF是边AB上的中线，且DC＝BF，DE⊥CF于点E．
（1）求证：E是CF的中点．
（2）若∠B＝30°，求∠BCF的度数．

（1）证明：如图，连接DF，
∵AD是边BC上的高，CF是边AB上的中线，
∴DF＝BF＝AB，
∵DC＝BF，
∴CD＝DF，
∵DE⊥CF，
∴E是CF的中点；
（2）解：由（1）的结论DF＝BF得∠FDB＝∠FBD＝30°，
∵DC＝DF，
∴∠DCF＝∠DFC，
由外角的性质得∠FDB＝∠DCF+∠DFC＝2∠DCF，
∴∠FBD＝2∠DCF，
即∠BCF＝∠B＝15°．

24．（10分）甲、乙两地间的直线公路长为400千米．一辆轿车和一辆货车分别沿该公路从甲、乙两地以各自的速度匀速相向而行，货车比轿车早出发1小时，途中轿车出现了故障，停下维修，货车仍继续行驶．1小时后轿车故障被排除，此时接到通知，轿车立刻掉头按原路原速返回甲地（接到通知及掉头时间不计）．最后两车同时到达甲地，已知两车距各自出发地的距离y（千米）与轿车所用的时间x（小时）的关系如图所示，请结合图象解答下列问题：
（1）货车的速度是 　50　千米/小时；轿车的速度是 　80　千米/小时；t值为 　3　．
（2）求轿车距其出发地的距离y（千米）与所用时间x（小时）之间的函数关系式并写出自变量x的取值范围；
（3）请直接写出货车出发多长时间两车相距90千米．

解：（1）货车的速度是50千米/小时；
货车所用时间为400÷50＝8小时，
∴轿车的速度是：480÷（7﹣1）＝80千米/小时；t＝240÷80＝3．
答案：50；80；3；
（2）由题意可知：A（3，240），B（4，240），C（7，0），
设直线OA的解析式为y＝k1x（k1≠0），
∴y＝80x（0≤x＜3），
当3≤x≤4时，y＝240，
设直线BC的解析式为y＝k2x+b（k≠0），
把B（4，240），C（7，0）代入得：
，解得，
∴y＝﹣80x+560（4＜x≤7）
∴y＝；
（3）设货车出发x小时两车相距90千米，
当≤4时，50x+80（x﹣1）+90＝400，
解得x＝3；
当x≥5时 50x﹣（400﹣240）＝80（x﹣1﹣4）+90，
解得x＝5．
综上所述，当货车出发3小时或5小时后两车相距90千米．
25．（12分）如图，△ABC中，∠ACB＝90°，AB＝10，BC＝6，若点P从点A出发，以每秒1个单位长度的速度沿折线A﹣C﹣B﹣A运动，设运动时间为t秒（t＞0）．

（1）若点P在AC上，且满足PA＝PB时，求此时t的值；
（2）若点P恰好在∠BAC的平分线上，求t的值．
解：（1）如图1，PA＝PB，

在Rt△ACB中，
设AP＝t，则PC＝8﹣t，
在Rt△PCB中，依勾股定理得：（8﹣t）2+62＝t2，
解得，
即此时t的值为；
（2）分两种情况：
①点P在BC上时，如图2所示：过点P作PE⊥AB，

则PC＝t﹣8，PB＝14﹣t，
∵AP平分∠BAC
且PC⊥AC
∴PE＝PC
在△ACP与△AEP中，，
∴△ACP≌△AEP（AAS），
∴AE＝AC＝8，
∴BE＝2，
在Rt△PEB中，依勾股定理得：PE2+EB2＝PB2
即：（t﹣8）2+22＝（14﹣t）2
解得：；
②点P又回到A点时，
∵AC+BC+AB＝8+6+10＝24，
∴t＝24；
综上所述，点P在∠BAC的平分线上时，t的值为秒或24秒．