八年级数学北师大版上册 第五章 二元一次方程组复习 课件1

这是一份八年级数学北师大版上册 第五章 二元一次方程组复习 课件1，共18页。
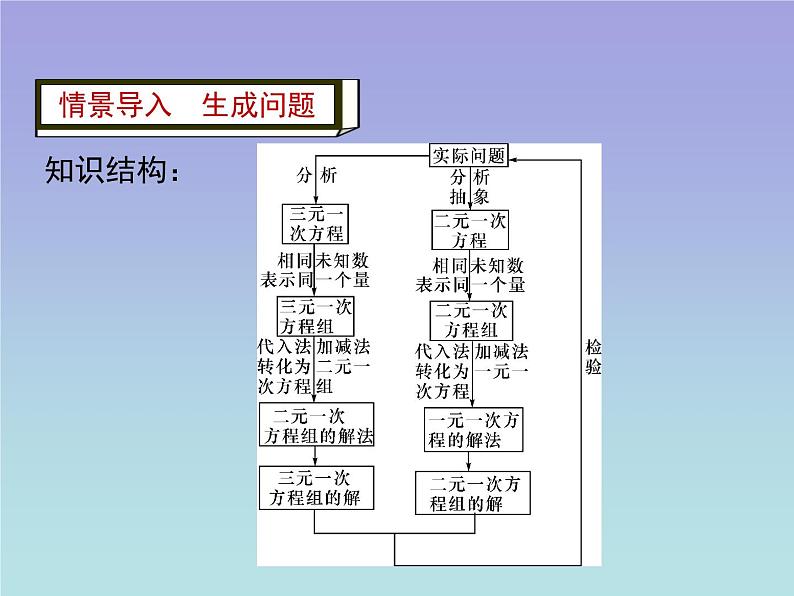
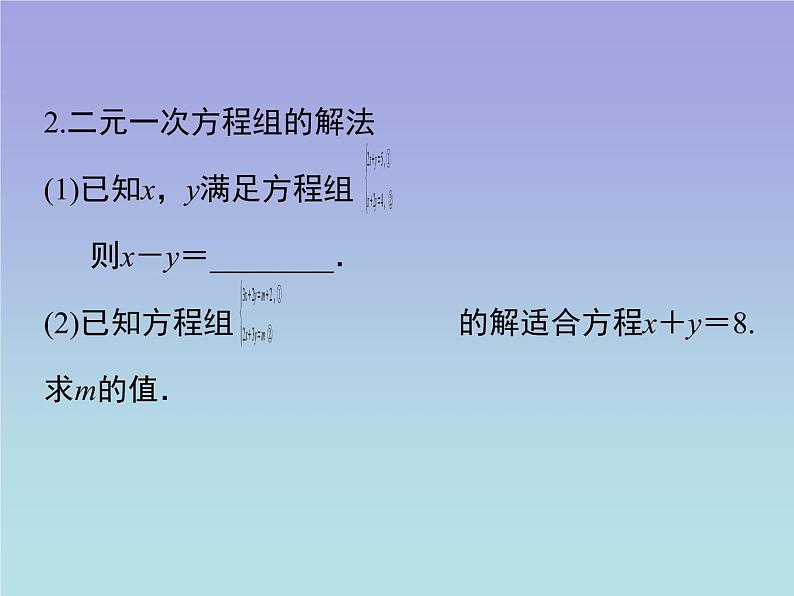
本章复习小结第五章 二元一次方程组1．会解二元一次方程组和利用二元一次方程组解决实际问题．2．通过归纳整理本章知识点，回顾解决问题中所涉及的整体代入、转化消元、数形结合的思想．加强各知识之间的内在联系，便于加深理解．学习目标【学习重点】会解二元一次方程组，能够根据具体问题中的数量关系列出方程组．【学习难点】列方程组解应用性的实际问题．情景导入　生成问题知识结构：自学互研　生成能力知识模块一　知识清单　加深理解1．二元一次方程的概念含有两个未知数，并且含有未知数的项的次数都是1，同时还必须是整式方程才叫做二元一次方程．【说明】　第(1)题并不一定要先把x，y的值求出来，再计算x－y的值．可以采用①－②直接求得；第(2)题也并不一定是用m的代数式来表示x，y，再代入x＋y＝8求得m，可以①＋②得5(x＋y)＝2m＋2，即x＋y＝ ，由x＋y＝8，得 ＝8，可求得m.【归纳结论】　解方程组时，可以根据方程组的特点灵活求解，使计算简便，切不可生搬硬套．3．列方程组解决实际问题在用方程组解决问题的过程中要注意以下几个方面：①审清题意，找等量关系是关键；②单位要统一；③符合实际意义；④检验．知识模块二　典例引路　全面复习例1：解方程组分析：本题考查用加减法解二元一次方程组，相同未知数的系数的差都是1，可反复利用加减消元法．解：由①－②，得z－y＝1③，由③×2012－②，得z＝－2.把z＝－2代入③，得－2－y＝1，y＝－3.例2：某工厂有甲、乙两条生产线先后投产，在乙生产线投产以前，甲生产线已生产了200吨成品，从乙生产线投产开始，甲、乙两条生产线每天分别生产20吨和30吨成品．(1)分别求出甲、乙两条生产线投产后，各自的总产量y(吨)与从乙开始投产后所用时间x(天)之间的函数关系式，并求出第几天结束后，甲、乙两生产线的总产量相同；(2)在直角坐标系中作出上述两个函数在第一象限内的图象，观察图象，分别指出第15天和第25天结束时，哪条生产线的总产量高．分析：此题涉及求解析式及函数与方程的关系，并利用一次函数的图象解决实际问题．解：(1)由题意可知，甲生产线生产时对应的函数关系式为y＝20x＋200.乙生产线生产时对应的函数关系式为y＝30x .令20x＋200＝30x，解得x＝20.∴当第20天结束时， 两条生产线的总产量相同；(2)由(1)可知，甲生产线所对应的函数图象一定经过两点A(0，200)，B(20，600)，乙生产线所对应的函数图象一定经过两点O(0，0)和B(20，600)，画出两个函数图象如图所示．由图象可知，第15天结束时，甲生产线的总产量高； 第25天结束时，乙生产线的总产量高．相关概念1.二元一次方程:通过化简后,只有两个未知数,并且所含未知数的项的次数都是1,系数都不是0的整式方程,叫做二元一次方程.2.二元一次方程的解:使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解.3.二元一次方程组:由两个一次方程组成,共有两个未知数的方程组,叫做二元一次方程组.深度归纳4.二元一次方程组的解:二元一次方程组中各个方程的公共解,叫做二元一次方程组的解.5.方程组的解法根据方程未知数的系数特征确定用哪一种解法.基本思想或思路——消元常用方法————代入法和加减法用代入法解二元一次方程组 (1)求表达式：从方程组中选一个系数比较简单的方程，将此方程中的一个未知数，如y，用含x的代数式表示; (2)把这个含x的代数式代入另一个方程中，消去y，得到一个关于x的一元一次方程；(3)解一元一次方程，求出x的值;(4)再把求出的x的值代入变形后的方程，求出y的值.用加减法解二元一次方程组(1)利用等式性质把一个或两个方程的两边都乘以适当的数，变换两个方程的某一个未知数的系数，使其绝对值相等；(2)把变换系数后的两个方程的两边分别相加或相减，消去一个未知数，得一元一次方程；(3)解这个一元一次方程，求得一个未知数的值 ；(4)把所求的这个未知的值代入方程组中较为简便的一个方程，求出另一个未知数，从而得到方程组的解 .列二元一次方程解决实际问题的一般步骤 审： 设： 列： 解： 答：审清题目中的等量关系． 设未知数． 根据等量关系，列出方程组． 解方程组，求出未知数． 检验所求出未知数是否符合题意，写出答案． 二元一次方程与一次函数二元一次方程组和一次函数的图象的关系方程组的解是对应的两条直线的交点坐标两条线的交点坐标是对应的方程组的解二元一次方程和一次函数的图象的关系以二元一次方程的解为坐标的点都在对应的函数图象上.一次函数图象上的点的坐标都适合对应的二元一次方程.再见