江苏地区2022学年七年级上学期数学期末真题典型考点【填空60道】-（原卷版）

江苏地区2022学年七年级上学期数学期末真题典型考点【填空60道】

1．若，则的值是________.

2．如果一个角是，那么这个角的余角是___________.

3．某商品的进价为每件100元，按标价打八折售出后每件可获利20元，则该商品的标价为每件____元．

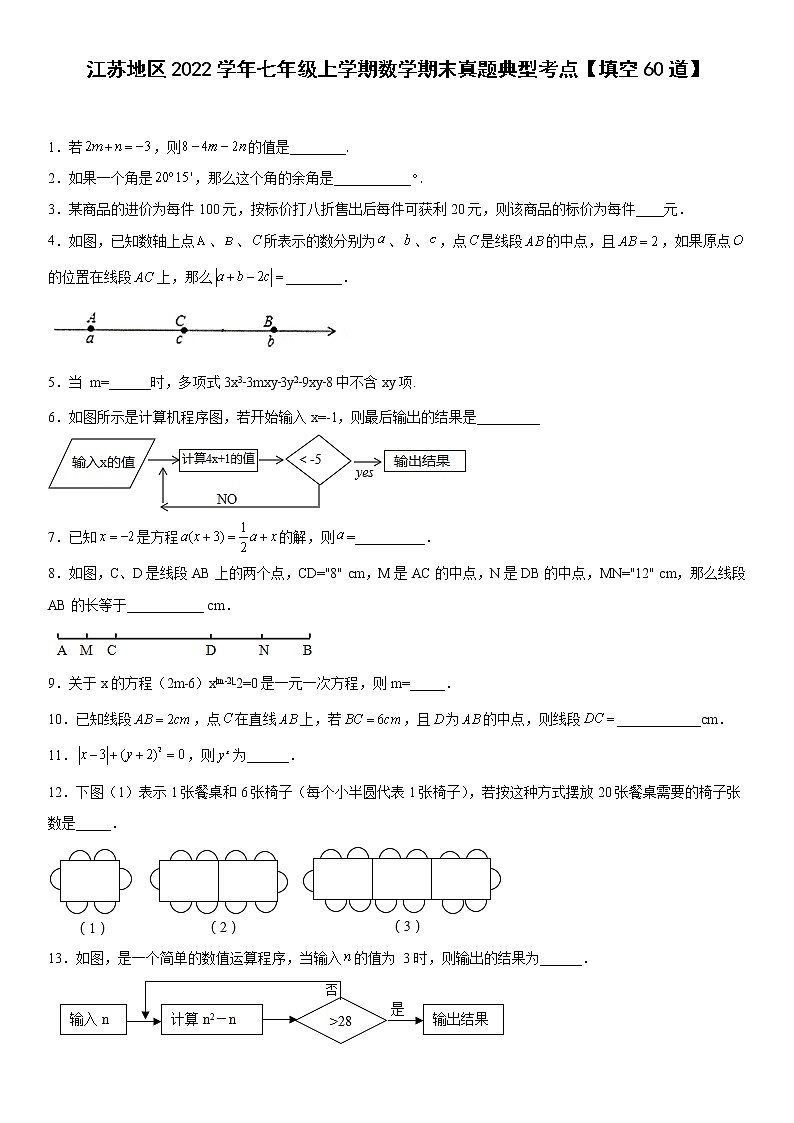
4．如图，已知数轴上点、、所表示的数分别为、、，点是线段的中点，且，如果原点的位置在线段上，那么________．

5．当 m=______时，多项式3x3﹣3mxy﹣3y2﹣9xy﹣8中不含xy项.

6．如图所示是计算机程序图，若开始输入x=-1，则最后输出的结果是_________

7．已知是方程的解，则=__________．

8．如图，C、D是线段AB上的两个点，CD="8" cm，M是AC的中点，N是DB的中点，MN="12" cm，那么线段AB的长等于___________ cm．

9．关于x的方程（2m﹣6）x|m﹣2|﹣2=0是一元一次方程，则m=_____．

10．已知线段，点在直线上，若，且为的中点，则线段____________cm．

11．，则为______．

12．下图（1）表示1张餐桌和6张椅子（每个小半圆代表1张椅子），若按这种方式摆放20张餐桌需要的椅子张数是_____．

13．如图，是一个简单的数值运算程序，当输入的值为 3时，则输出的结果为______．

14．单项式的系数是____；若与是同类项，则m+n= _______.

15．如果一个角的补角是150°，那么这个角的余角的度数是__________．

16．八点三十分时，钟表上时针与分针的夹角为______°．

17．我市溱潼会船节时举行划龙舟大赛，有16个队共352人参加．已知每个队一条船，每条船上人数相等，且每条船上有1人击鼓，1人掌舵，其余的人同时划桨．设每条船上划桨的有x人，那么可列出一元一次方程为_____________．

18．已知a＋b＝0，a≠b，则(a＋1)＋(b＋1)＝__________．

19．一个角的补角加上后，等于这个角的余角的倍，则这个角是____________．

20．近似数3.50万精确到_______位，2948000000保留两个有效数字是__________，5.028精确到百分位的近似数是___

21．如图，两块三角板的直角顶点O重叠在一起，且OB恰好平分∠COD，则∠AOD的度数是____度．

22．如图，已知线段AB＝4，延长线段AB到C，使BC＝2AB，点D是AC的中点，则DC的长等于________．

23．如图OA⊥OB，∠BOC＝40°，OD平分∠AOC，则∠BOD的度数是_____°

24．若单项式2x2ym与－xny3是同类项，则m+n的值是______．

25．如图，将一副三角板的直角顶点重合，摆在桌面上，若，则______度

26．一家商店将某种服装按成本价提高后标价，又以8折优惠卖出，结果每件仍获利15元，这种服装每件的成本为__________元．

27．如果关于的方程和方程的解相同，那么的值________．

28．一个角的余角的补角是121°15′，这个角的度数是__________．

29．如图所示是计算机某计算程序，若开始输入x＝﹣1，则最后输出的结果是_____．

30．的相反数是______，的倒数是______，的绝对值为______．

31．单项式的次数是____次．

32．若2a﹣b=2，则6﹣8a+4b=_____．

33．已知（a2﹣1）x2+ax+x﹣1＝0是关于x的一元一次方程，则a的值是 _____．

34．用铝片做听装饮料瓶，现有100张铝片，每张铝片可制瓶身16个或瓶底45个，一个瓶身和两个瓶底可配成一套.用多少张制瓶身，多少张制瓶底可以正好制成配套的饮料瓶？设用x张铝片制瓶身，则可列方程为____________.

35．一张长方形纸条折成如图的形状，若，则_______．

36．若，化简的结果是_______．

37．如图，、是内的两条射线，平分，平分，若，，则_______°（用含m、n的代数式表示）．

38．某项工作甲单独做8天完成，乙单独做12天完成，若甲先做3天，然后甲、乙合作完成此项工作，则甲一共做了__________天，

39．某正方体的平面展开图如图所示，已知该正方体相对两个面上的数互为相反数，则__________．

40．如图，将一个三角板60°角的顶点与另一个三角板的直角顶点重合，∠1＝27°，∠2＝_____．

41．如图所示的运算程序中，若开始输入的x值为96，我们发现第一次输出的结果为48，第二次输出的结果为24，…，则第2022次输出的结果为 _____．

42．一块手表上午6点45分，此时时针分针所夹锐角的大小为__________度．

43．如图，点A在数轴上表示的数是-8，点B在数轴上表示的数是16；线段的中点表示的数是__________，若点是数轴上的一个动点，当时，点表示的数是__________．

44．如图，已知∠AOB＝2∠BOC，OD平分∠AOC，且∠BOD＝20°，则∠AOC的度数为______°．

45．在纸上画一条数轴，将这张纸对折后，若该数轴上表示4的点与表示﹣1的点恰好重合，则此时与表示﹣3的点重合的点表示的数是______．

46．已知太阳的半径约为696 000 000m，696 000 000这个数用科学记数法可表示为________．

47．平面内不同的两点确定一条直线，不同的三点最多确定三条直线，则平面内不同的n个点最多可确定_____条直线（用含有n的代数式表示）．

48．已知点、在数轴上，点表示的数为-5，点表示的数为15.动点从点出发，以每秒3个单位长度的速度沿数轴正方向匀速移动，则点移动__________秒后，．

49．若a、b为实数，且，则的值是____．

50．如图，点C是线段AB的中点，点D在线段AB上，且AD＝AB，DC＝2cm，那么线段AB的长为________cm．

51．如图，将一副三角板的直角顶点重合，摆放在桌面上，当∠AOC＝__________时，AB所在直线与CD所在直线互相垂直．

52．某班学生分组参加活动，原来每组8人，后来重新编组，每组6人，这样比原来增加了两组，这个班共有多少名学生？若设共有x名学生，可列方程为________．

53．一个角比它的补角少40°，则这个角是______度．

54．已知关于的代数式和的值都与字母的取值无关．则______．

55．如图，将一副三角板摆放在直线AB上，，，设，则用x的代数式表示的度数为_________．

56．已知n是关于x的方程的解，则的值为_________．

57．有理数、、在数轴上位置如图，则的值为 ______．

58．当x=5时，px3+qx+1=2019，则当x=-5时，px3+qx+1的值是______．

59．如图，一根绳子对折以后用线段表示，在线段的三等分点处将绳子剪短，若所得三段绳长的 最大长度为，则这根绳子原长为________．

60．某班在植树节时需完成一批植树任务，若由全班学生一起完成每人需植树8棵；若由女生单独完成每人需植树12棵，则由男生单独完成每人需植树_____棵．