河南省商丘市2022-2023学年八年级上学期期中数学试题(含答案)

2022—2023学年度第一学期期中测试卷

八年级数学（RJ）

一、选择题（每小题3分，共30分）

1．下列长度四根木棒中，能与长为4，9的两根木棒围成一个三角形的是（    ）

A．4 B．5 C．9 D．14

2．围棋起源于中国，古代称之为“弈”，至今已有四千多年的历史．下列由黑白棋子摆成的图案是轴对称图形的是（    ）

A． B． C． D．

3．等腰三角形一个角的度数为50°，则顶角的度数为（    ）

A．50° B．80° C．65° D．50°或80°

4．如果n边形的内角和是它外角和的3倍，则n等于（    ）

A．6 B．7 C．8 D．9

5．如图，已知点A、D、C、F在同一条直线上，AB＝DE，BC＝EF，要使，还需要添加一个条件是（    ）

A．∠BCA＝∠F B．∠B＝∠E C． D．∠A＝∠EDF

6．如图，小章家里有一块破碎的三角形玻璃，很快他就根据所学知识在纸上画了一个与原三角形一样的三角形，那么这两个三角形完全一样的依据是（    ）

A．SSS B．SAS C．AAS D．ASA

7．如图，BO、CO分别是∠ABC和∠ACB的平分线，BO与CO交于点O，过点O作交AB于点D，交AC于点E，已知AB＝6，AC＝4，则的周长是（    ）

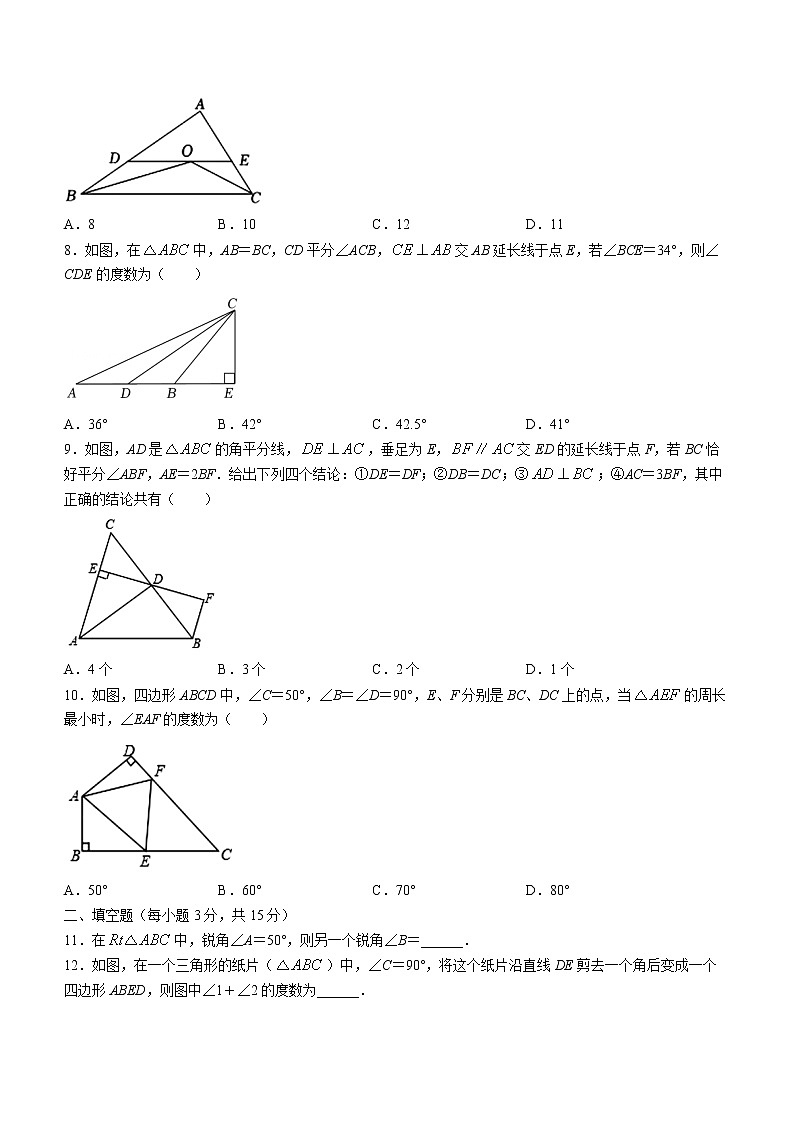
A．8 B．10 C．12 D．11

8．如图，在中，AB＝BC，CD平分∠ACB，交AB延长线于点E，若∠BCE＝34°，则∠CDE的度数为（    ）

A．36° B．42° C．42.5° D．41°

9．如图，AD是的角平分线，，垂足为E，交ED的延长线于点F，若BC恰好平分∠ABF，AE＝2BF．给出下列四个结论：①DE＝DF；②DB＝DC；③；④AC＝3BF，其中正确的结论共有（    ）

A．4个 B．3个 C．2个 D．1个

10．如图，四边形ABCD中，∠C＝50°，∠B＝∠D＝90°，E、F分别是BC、DC上的点，当的周长最小时，∠EAF的度数为（    ）

A．50° B．60° C．70° D．80°

二、填空题（每小题3分，共15分）

11．在中，锐角∠A＝50°，则另一个锐角∠B＝______．

12．如图，在一个三角形的纸片（）中，∠C＝90°，将这个纸片沿直线DE剪去一个角后变成一个四边形ABED，则图中∠1＋∠2的度数为______．

13．如图，在中，，，垂足分别为D，E，AD与CE交于点F，请你添加一个适当的条件：______，使．

14．如图，中，∠C＝90°，AC＝8cm，BC＝15cm，AB＝17cm，∠CAB与∠CBA的角平分线相交于点O，过点O作，垂足为点D，则线段OD的长为______cm．

15．已知等腰中，，且，则等腰的顶角度数为______．

三、解答题（共8题，共75分）

16．（9分）如图，AC和BD交于点O，∠A＝∠D＝90°，AC＝BD．求证：OA＝OD．

17．（9分）如图所示，AE为的角平分线，CD为的高，若∠B＝30°，∠ACB为70°．

（1）求∠CAF的度数；

（2）求∠AFC的度数．

18．（9分）（1）请画出关于y轴对称的（其中，，分别是A，B，C的对应点）；

（2）直接写出三点的坐标：______，______，______．

（3）直接写出的面积是______．

19．（9分）已知：如图，在中，AC＜AB且∠C＝2∠B．

（1）用直尺和圆规作出一条过点A的直线l，使得点C关于直线的对称点落在边AB上（不写作法，保留作图痕迹）

（2）设（1）中直线l与边BC的交点为D，请写出线段AB、AC、CD之间的数量关系并说明理由．

20．（9分）已知边数为n的多边形的一个外角是m°，内角和是x°，外角和是y°．

（1）当x＝2y时，求n的值；

（2）若x＋y＋m＝2380，求m的值．

21．（9分）如图，四边形ABCD中，AB＝BC＝2CD，，∠C＝90°，E是BC的中点，AE与BD相交于点F，连接DE．

（1）求证：；

（2）判断线段AE与BD的数量关系及位置关系，并说明理由．

22．（10分）如图，在中，∠C＝90°，∠A＝30°，BC＝12cm．动点P从点A出发，沿AB向点B运动，动点Q从点B出发，沿BC向点C运动，如果动点P以2cm/s，Q以1cm/s的速度同时出发，设运动时间为t（s），解答下列问题：

（1）t为多少时，是等边三角形？

（2）P、Q在运动过程中，的形状不断发生变化，当t为多少时，是直角三角形？请说明理由．

23．（11分）如图，中，∠ACB＝90°，AC＝BC，E点为射线CB上一动点，连接AE，作且AF＝AE．

（1）如图1，过F点作交AC于D点，求证：FD＝BC；

（2）如图2，连接BF交AC于G点，若AG＝3，CG＝1，求证：E点为BC中点；

（3）当E点在射线CB上，连接BF与直线AC交于G点，若BC＝4，BE＝3，则______（直接写出结果）

2022—2023学年度第一学期期中测试卷（二）参考答案

八年级数学（RJ）

一、选择题（每小题3分，共30分）

1．C   2．A   3．D   4．C   5．B   6．D   7．B   8．B   9．A   10．D

二、填空题（每小题3分，共15分）

11．40°    12．270°    13．AB＝BC（答案不唯一）    14．3   15．90°或30°或150°

三、解答题（共8题，共75分）

16．证明：∵∠A＝∠D＝90°，在与中，，

∴，∴∠ACB＝∠DBC，∴∠OCB＝∠OBC，∴OB＝OC，

∵AC＝BD，∴AC－OC＝BD－OB，即OA＝OD．

17．解：（1）∵∠B＝30°，∠ACB＝70°，∴∠BAC＝180°－30°－70°＝80°，

又∵AE平分∠BAC，∴；

（2）∵CD为的高，∠CAD＝80°，∴中，∠ACF＝90°－80°＝10°，

∴∠AFC＝180°－∠ACF－∠CAF＝180°－10°－40°＝130°．

18．解：（1）如图所示；

（2），，；

（3）的面积：．

19．解：（1）如图所示，直线AD即为所求；

（2）线段AB、AC、CD之间的数量关系为：AB＝AC＋CD．

理由：由题可得，AE＝AC，∠CAD＝∠EAD，AD＝AD，

∴，∴DE＝CD，∠AED＝∠C＝2∠B，

又∵∠AED＝∠B＋∠BDE，∴∠B＝∠BDE，∴BE＝DE＝CD，

又∵AB＝AE＋BE，∴AB＝AC＋CD．

20．解：（1）∵多边形的外角和为360°，∴y＝360，

∵n边形的内角和为（n－2）×180°，∴x＝（n－2）×180＝180n－360，

∵x＝2y，∴180n－360＝2×360，∴n＝6．

（2）∵x＋y＋m＝2380，∴180n－360＋360＋m＝2380，即180n＋m＝2380，

∵n边形的一个外角是m°，∴m＜180，

∵n为正整数，∴n为2380÷180的整数部分，m为2380÷180的余数，

∵2380÷180＝13…40，∴m＝40．

21．（1）证明：∵，∴∠ABE＋∠C＝180°，∵∠C＝90°，∴∠ABE＝90°＝∠C，

∵E是BC的中点，∴BC＝2BE，∵BC＝2CD，∴BE＝CD，

在和中，，∴；

（2）解：AE＝BD，，理由如下：由（1）得：，∴AE＝BD，

∵∠BAE＝∠CBD，∠ABF＋∠CBD＝90°，∴∠ABF＋∠BAE＝90°，∴∠AFB＝90°，∴．

22．解：（1）要使是等边三角形，即可得：PB＝BQ，

在中，∠C＝90°，∠A＝30°，BC＝12cm．∴AB＝24cm，

可得：PB＝（24－2t）cm，BQ＝t cm，即24－2t＝t，解得：t＝8，

（2）当t为6s或时，是直角三角形，理由如下：

∵∠C＝90°，∠A＝30°，BC＝12cm，∴AB＝2BC＝12×2＝24（cm），

∵动点P以2cm/s，Q以1cm/s的速度出发，∴BP＝AB－AP＝（24－2t）cm，BQ＝t cm，

∵是直角三角形，∴BP＝2BQ或BQ＝2BP，

当BP＝2BQ时，24－2t＝2t，解得t＝6；当BQ＝2BP时，t＝2（24－2t），解得．

所以，当t为6s或时，是直角三角形．

23．（1）证明：∵，∴∠FDA＝90°，∴∠DFA＋∠DAF＝90°，

同理，∠CAE＋∠DAF＝90°，∴∠DFA＝∠CAE，

在和中，，∴，

∴DF＝AC，∵AC＝BC，∴FD＝BC；

（2）作于D，由（1）得，FD＝AC＝BC，AD＝CE，

在和中，，∴，

∴DG＝CG＝1，∴AD＝2，∴CE＝2，∵BC＝AC＝AG＋CG＝4，∴E点为BC中点；

（3）或．

【提示】当点E在CB的延长线上时，过F作的延长线交于点D，

BC＝AC＝4，CE＝CB＋BE＝7，

由（1）（2）知：，，

∴CG＝GD，AD＝CE＝7，∴CG＝DG＝1.5，∴，

同理，当点E在线段BC上时，，故答案为：或．