湖北省十堰市张湾区2022-2023学年七年级（上）数学期末模拟测试(解析版)

十堰市张湾区2022-2023学年七年级（上）数学期末模拟测试

一、选择题（本题共10个小题，每小题3分，共 30分。下列各题，每小题只有一个选项符合题意。）

1. 在0，2，－2，－3.5这四个数中，是负整数的是（   ）

A. 0 B. 2 C. －2 D. －3.5

2. 把数3160000用科学记数法表示成3.16×10n，则正整数n为 （ ）

A 4 B. 5 C. 6 D. 7

3. 某学习小组送给医务工作者的正方体6面上都有一个汉字，如图所示是它的一种展开图，那么在原正方体中，与“最”字所在面相对的面上的汉字是（   ） 

A. 美               B. 的                                

C. 逆               D.人

4. 将一副三角尺按不同位置摆放，摆放方式中∠α 与∠β 互余的是（   ）

A.  B.

C.  D.

5. 将一副三角板按如图所示的方式放置，则∠AOB的大小为（　　）

A. 75° B. 45° C. 30° D. 15°

6. 下列各组单项式中，不是同类项的一组是（　　　）

A 和 B. 和3 

C. 和－ D. 和

7. 2条直线相交，有1个交点；3条直线相交，最多有3个交点；n条直线相交最多有多少个交点？（    ）

A.  B.  

C.  D.

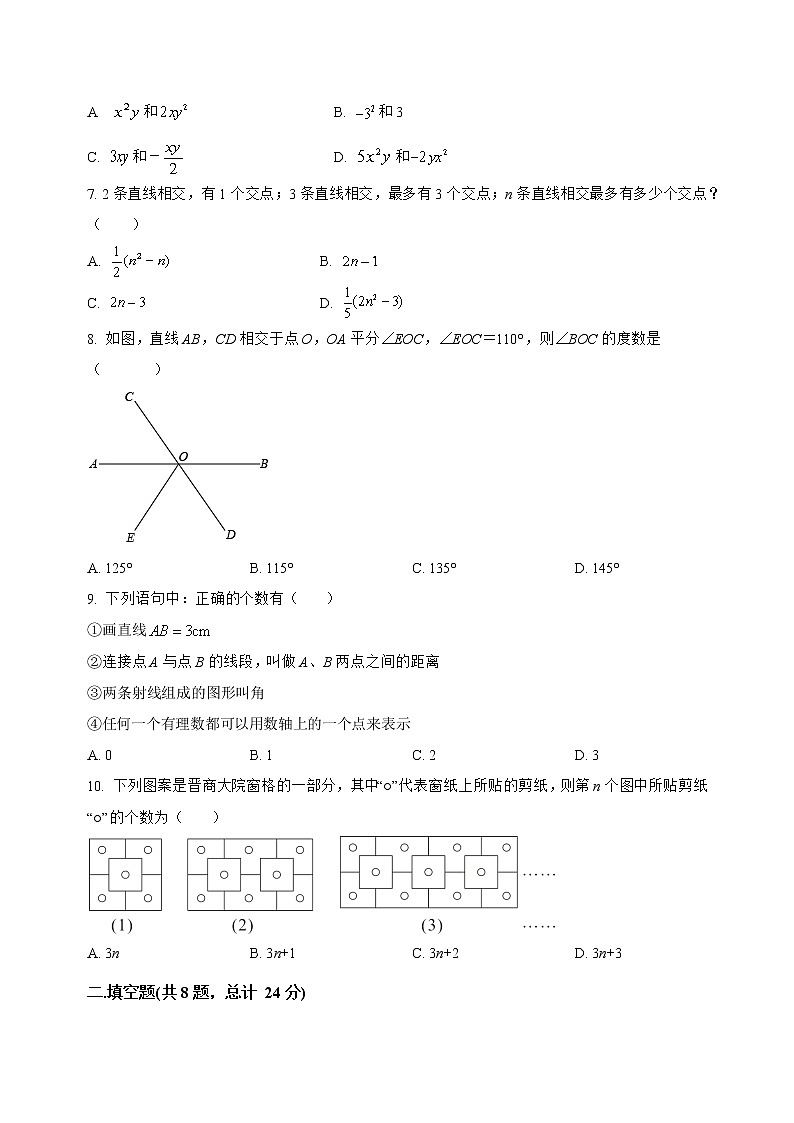
8. 如图，直线AB，CD相交于点O，OA平分∠EOC，∠EOC＝110°，则∠BOC的度数是（       ）

A. 125° B. 115° C. 135° D. 145°

9. 下列语句中：正确的个数有（    ）

①画直线

②连接点A与点B的线段，叫做A、B两点之间的距离

③两条射线组成的图形叫角

④任何一个有理数都可以用数轴上的一个点来表示

A. 0 B. 1 C. 2 D. 3

10. 下列图案是晋商大院窗格的一部分，其中“○”代表窗纸上所贴的剪纸，则第n个图中所贴剪纸“○”的个数为（　　）

A. 3n B. 3n+1 C. 3n+2 D. 3n+3

二.填空题(共8题，总计 24分)

11. 我市某天的最高气温是8℃，最低气温是－3℃，那么这天的温差是______℃．

12. 已知线段AB=8cm，点C在直线AB上，BC=3cm，则线段AC长为________.

13. 若代数式x－3y的值是2，则代数式2x-6y+1的值是_____．

14. 已知线段AB=10cm,点C是直线AB上一点, BC=4cm,若M是AB的中点, N是BC的中点，则线段MN的长度是________cm.

15. a表示一个一位数，b表示一个两位数，如果把a放在b的右边组成一个三位数，则这个三位数是_________．

16. 如图是一个长方体的展开图，写出其中一组相对的面（写一对即可）______．

17. 已知，且，则_____________

18. 如图①，为直线上一点，作射线，使，将一个直角三角尺如图摆放，直角顶点在点处，一条直角边在射线上．将图①中的三角尺绕点以每秒的速度按逆时针方向旋转（如图②所示），在旋转一周的过程中，第秒时，所在直线恰好平分，则的值为________．

三.解答题(共8题，总计66分)

19. 已知a，b互为相反数，c、d互为倒数，x的绝对值是3，求的值．

20. 解方程：

（1）2x＋3＝5x﹣18

（2）．

21. 求a、b满足什么条件时，多项式与多项式的差是单项式．

22. 如图，在“和谐”公园的绿茵广场上有A，B，C三棵树．测得B树和C树相距100m，，，请用代表20m，画出类似的图形，量出，的长（精确到），再换算出A树距B，C两树的实际距离．

23. 一艘船从甲码头到乙码头顺流而行，用了2.5 h；从乙码头返回甲码头逆流而行，用了3 h．已知水流的速度是2 km/h，求船在静水中的平均速度．

24. 如图，已知∠AOB=40°，∠BOC=3∠AOB，OD平分∠AOC，求∠COD的度数．

解：因为∠BOC=3∠AOB，∠AOB=40°，

所以∠BOC=     °．

所以∠AOC=     +     =     °+     °=     °．

因为OD平分∠AOC，

所以∠COD=      =×      °=     °．

25. 如图是一种单肩包，其背带由双层部分、单层部分和调节扣构成．背带的长度（单层部分与双层部分长度的和，其中调节扣所占长度忽略不计）可以通过调节扣调节，经测量，得到下列数据．

（1）根据数据规律，将表格补充完整：______；______；

（2）设双层部分的长度为xcm，请用x的代数式表示单层部分的长度．

（3）当背带的长度调为130cm时，此时双层部分的长度为多少cm？

（4）试求背带长度的最大值与最小值．

26. 问题情境

在综合与实践课上，老师让同学们以“两条平行线AB，CD和一块含60°角的直角三角尺EFG（∠EFG＝90°，∠EGF＝60°）”为主题开展数学活动．

操作发现

（1）如图（1），小明把三角尺的60°角的顶点G放在CD上，若∠2＝2∠1，求∠1的度数；

（2）如图（2），小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上，请你探索并说明∠AEF与∠FGC之间的数量关系；

结论应用

（3）如图（3），小亮把三角尺的直角顶点F放在CD上，30°角的顶点E落在AB上．若，则∠CFG等于______（用含的式子表示）．

十堰市张湾区2022-2023学年七年级（上）数学期末模拟测试

参考答案及解析

一.选择题

1.【答案】：C

【解析】：解：在0，2，－2，－3.5这四个数中，是负整数的是-2，

故选C．

2.【答案】：C

【解析】：把一个比较大的数表达成的形式，叫科学记数法.其中，为正整数，且为这个数的整数位减1. . 故选C.

考点：科学记数法.

3.【答案】：D

【解析】：解：由正方体的展开图可知: “美”和“逆”所在面是相对面，“的”和“行”所在面是相对面，“最”和“人”所在面是相对面，

故与“最”字所在面相对的面上的汉字是“人”.

故答案为：D.

4.【答案】：C

【解析】：解：A、∠α与∠β不互余，故本选项错误；
B、∠α与∠β不互余，故本选项错误；
C、∠α与∠β互余，故本选项正确；
D、∠α与∠β不互余，∠α和∠β互补，故本选项错误；
故选：C．

5.【答案】：D

【解析】：解：∠AOB＝45°﹣30°＝15°．

故选：D．

6.【答案】：A

【解析】：解：A.x2y和2xy2所含字母相同，但相同字母的指数不同，故不是同类项，符合题意；

B. - 32和3是两个常数，是同类项，故是同类项，不符合题意；

C.3xy和所含字母相同，相同字母的指数也相同，故是同类项，不符合题意；

C.5x2y和 - 2yx2所含字母相同，相同字母的指数也相同，故是同类项，不符合题意.

故选：A.

7.【答案】：A

【解析】：解：∵2条直线相交时，最多有1个交点；

3条直线相交时，最多有1+2=3个交点；

4条直线相交时，最多有1+2+3=6个交点；

…

∴5条直线相交时，最多有1+2+3+4=10个交点；

6条直线相交时，最多有1+2+3+4+5=15个交点；

7条直线相交时，最多有1+2+3+4+5+6=21个交点；

n条直线相交，交点最多有．

故选A．

8.【答案】：A

【解析】：解：∵OA平分∠EOC，∠EOC＝110°，

∴∠AOC=∠COE=55°

∵∠AOC+∠BOC是一个平角

∴∠BOC=180°-55°=125°

故选：A．

9.【答案】：B

【解析】：直线不可以度量，所以画直线AB=3cm是错误的；

连接点A与点B的线段的长度，叫做A、B两点之间的距离，原说法错误；

具有公共端点的两条射线组成的图形叫角，原说法错误；

任何一个有理数都可以用数轴上的点来表示，原说法正确；

故正确答案有1个，

故选：B．

10.【答案】：C

【解析】：解：第一个图案为3+2＝5个窗花；

第二个图案为2×3+2＝8个窗花；

第三个图案为3×3+2＝11个窗花；

……

由此得到：第n个图案所贴窗花数为（3n+2）个．

故选：C．

【点睛】本题主要考查了图形类规律题，明确题意，准确得到规律是解题的关键．

二. 填空题

11.【答案】： 11

【解析】：解：8﹣（﹣3）＝8+3＝11（℃）

答：这天的温差是11℃．

故答案为：11．

12.【答案】：5cm或者11cm

【解析】：①当C点在线段AB上时，C点在A、B两点之间，

此时cm，

∵线段cm，

∴cm；

②当C点在线段AB的延长线上时，

此时cm，

∵线段cm，

∴cm；

综上，线段AC的长为5cm或者11cm

13.【答案】：5

【解析】：解：由题意得：，

则，

故答案为：5．

14.【答案】：7或3.

【解析】：（1）当点C在线段AB上，MN=AB-BC=5-2=3

（2）当点C在线段AB的延长线上，MN=AB＋BC=5＋2=7，

故填7或3.

15.【答案】：

【解析】：解：根据题意得：这个三位数是．

故答案为：

16.【答案】：A和F，B和D，C和E

【解析】：根据长方体的展开图可知，相对面中间隔着一个面，

所以，A和F，B和D，C和E为相对面．

故答案为：A和F，B和D，C和E（写一对即可）．

17.【答案】： 或

【解析】：，

，

又，

或，

或，

故答案为：或．

18.【答案】： 12或30．

【解析】：解：∵∠AOC=120°，

∴∠BOC=60°

∵OQ所在直线恰好平分∠BOC，

∴∠BOQ=∠BOC=30°或∠BOQ=180°+30°=210°，

∴10t=30+90或10t=90+210，解得t=12或30．

故填：12或30．

三.解答题

19【答案】：

－22或8

【解析】：

解：根据题意，得，，，所以或．

当时，原式；

当时，原式．

故的值是－22或8．

20【答案】：

（1）x＝7；（2）x＝

【解析】：

解：（1）移项合并得：3x＝21，

解得：x＝7；

（2）去分母得：3x+9﹣13+3x＝6，

移项合并得：6x＝10，

解得：x＝．

21【答案】：

【解析】：

解：多项式与多项式的差为：

又因为多项式与多项式的差为单项式，

解得：

22【答案】：

图见解析，A树距B，C两树的实际距离分别是200m,173.2m.

【解析】：

解：如图，经测量可得：

AB≈100.0mm=10cm，AC≈86.6mm=8.66cm，

换算可知：A树距B树的实际距离为，

A树距C树的实际距离为．

23【答案】：

船在静水中的平均速度为22 km/h

【解析】：

设船在静水中的平均速度为x km/h，则顺流速度为km/h，逆流速度为km/h．

依题意，．

解得．

答：船在静水中的平均速度为22 km/h．

24【答案】：

120；∠AOB；∠BOC；40；120；160；∠AOC；160；80

【解析】：

解：因为∠BOC=3∠AOB，∠AOB=40°，

所以∠BOC=120°．

所以∠AOC=∠AOB+∠BOC=40°+120°=160°．

因为OD平分∠AOC，

所以∠COD= ∠AOC=× 160°=80°．

故答案为：120；∠AOB；∠BOC；40；120；160；∠AOC；160；80．

【点睛】本题考查了角平分线的定义和角的计算，能求出∠AOC的度数是解题关键．

25【答案】：

（1）112；32   

（2）   

（3）cm   

（4）最大值为152cm，最小值为76cm

【解析】：

【小问1详解】

根据数据，136=148-12；124 =136-12；则a=112=124-12；

8=2+6；14=8+6；20=14+6；26=20+6；则b=32=26+6

【小问2详解】

根据（1）得到规律：152-2×双层部分的长度=单层部分的长度

即单层部分的长度为：

【小问3详解】

由题意可得方程：

解得：

【小问4详解】

因为背带长为：当时，背带长的最大值为152cm，

当时，背带长的最小值为76cm．

26【答案】：

（1）∠1＝40°   

（2）∠AEF＋∠GFC＝90°；说明见解析   

（3）

【解析】：

（1）根据，可得∠1=∠EGD，再根据∠2=2∠1，∠FGE＝60°，即可得出∠EGD＝（180°−60°）＝40°，进而得到∠1＝40°；

（2）根据，可得∠AEG＋∠CGE＝180°，再根据∠FEG＋∠EGF＝90°，即可得到∠AEF＋∠FGC＝90°；

（3）依据，可得∠AEF＋∠CFE＝180°，再根据∠GFE＝90°，∠GEF＝30°，∠AEG＝α，即可得到∠GFC＝180°−90°−30°−α＝60°−α．

【小问1详解】

如图（1）．

∵，

∴∠1＝∠EGD．

又∵∠2＝2∠1，

∴∠2＝2∠EGD．

又∵∠FGE＝60°，

∴，

∴∠1＝40°；

【小问2详解】

解：∠AEF＋∠GFC＝90°，

理由：如图（2）．

∵，

∴∠AEG＋∠CGE＝180°，

即∠AEF＋∠FEG＋∠EGF＋∠FGC＝180°．

又∵∠FEG＋∠EGF＝90°，

∴∠AEF＋∠GFC＝90°；

【小问3详解】

解：如图（3）．

∵，

∴∠AEF＋∠CFE＝180°，

即∠AEG＋∠FEG＋∠EFG＋∠GFC＝180°．

又∵∠GFE＝90°，∠GEF＝30°，∠AEG＝α，

∴．

故答案为．

【点睛】本题主要考查了平行线的性质的运用，解决问题的关键是掌握：两直线平行，同旁内角互补．