人教版（中职）基础模块上册4.1 指数与指数函数教学设计

这是一份人教版（中职）基础模块上册4.1 指数与指数函数教学设计，共4页。教案主要包含了教学目标，教学重点，教学难点，教学方法，教学过程等内容，欢迎下载使用。

【教学目标】
1. 了解根式的概念和性质； 理解分数指数幂的概念；掌握有理数指数幂的运算性质．
2. 会对根式、分数指数幂进行互化．培养学生的观察、分析、归纳等逻辑思维能力．
3. 培养学生用事物之间普遍联系的观点看问题．
【教学重点】
分数指数幂的概念以及分数指数幂的运算性质．
【教学难点】
对分数指数幂概念的理解．
【教学方法】
这节课主要采用问题解决教学法．
在引入分数指数幂时，先讲方根的概念，根据方根的定义，得到根式具有的性质．在利用根式的运算性质对根式的化简过程中，引导学生注意发现并归纳其变形特点，进而由特殊情形归纳出一般规律．在对根式的性质进行练习以后，为了解决运算的合理性，引入了分数指数幂的概念，从而将指数幂推广到了有理数范围．在学生掌握了有理指数幂的运算性质后，将有理指数幂推广到实数指数幂．考虑到职校学生的实际情况，并没有给出严格的推证．
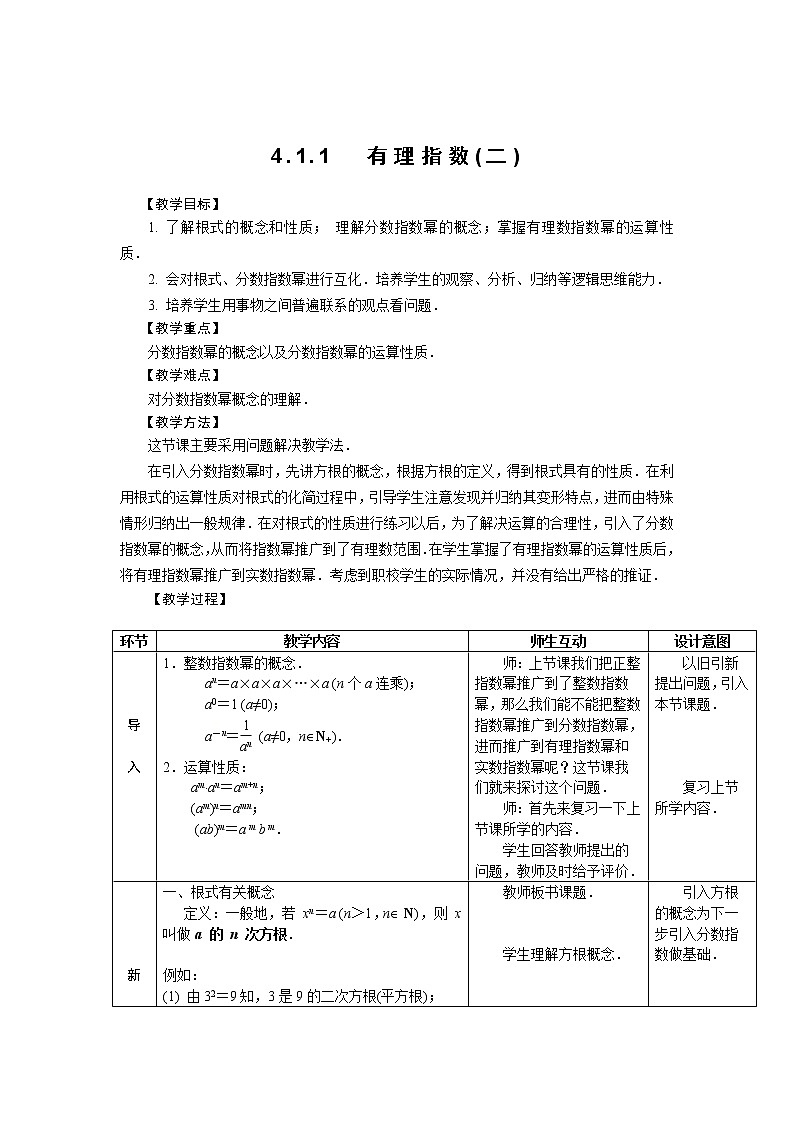
【教学过程】
环节
教学内容
师生互动
设计意图
导
入
1．整数指数幂的概念．
an＝a×a×a×…×a (n个a连乘)；
a0＝1 (a≠0)；
a－n＝ EQ \F(1,an) (a≠0，nN+)．
2．运算性质：
aman＝am+n；
(am)n＝amn；
(ab)m＝a m b m．
师：上节课我们把正整指数幂推广到了整数指数幂，那么我们能不能把整数指数幂推广到分数指数幂，进而推广到有理指数幂和实数指数幂呢？这节课我们就来探讨这个问题．
师：首先来复习一下上节课所学的内容．
学生回答教师提出的问题，教师及时给予评价．
以旧引新提出问题，引入本节课题．
复习上节所学内容．
新
课
新
课
新
课
一、根式有关概念
定义：一般地，若 xn＝a (n＞1，nN)，则 x 叫做a 的 n 次方根．
例如：
(1) 由32＝9知，3是9的二次方根(平方根)；
由(－3)2＝9知，－3也是9的二次方根(平方根)；
(2) 由(－5)3＝－125知，－5是－125的三次方根(立方根)；
(3) 由64＝1 296知，6是1 296 的4次方根．
有关结论：
(1) 当n为奇数时：正数的n次方根为正数，负数的n次方根为负数．记作：
x＝ EQ \R(n,a)．
(2) 当n为偶数时，正数的n次方根有两个(互为相反数)．记作：
x＝± EQ \R(n,a)．
(3) 负数没有偶次方根．
(4) 0的任何次方根都为0．
当 EQ \R(n,a)有意义时， EQ \R(n,a)叫做根式，n叫根指数．
正数a的正n次方根叫做a的n次算术根．
例如： EQ \R(3,2)叫做2的3次算术根； EQ \R(4,－2)不叫根式，因为它是没有意义的．
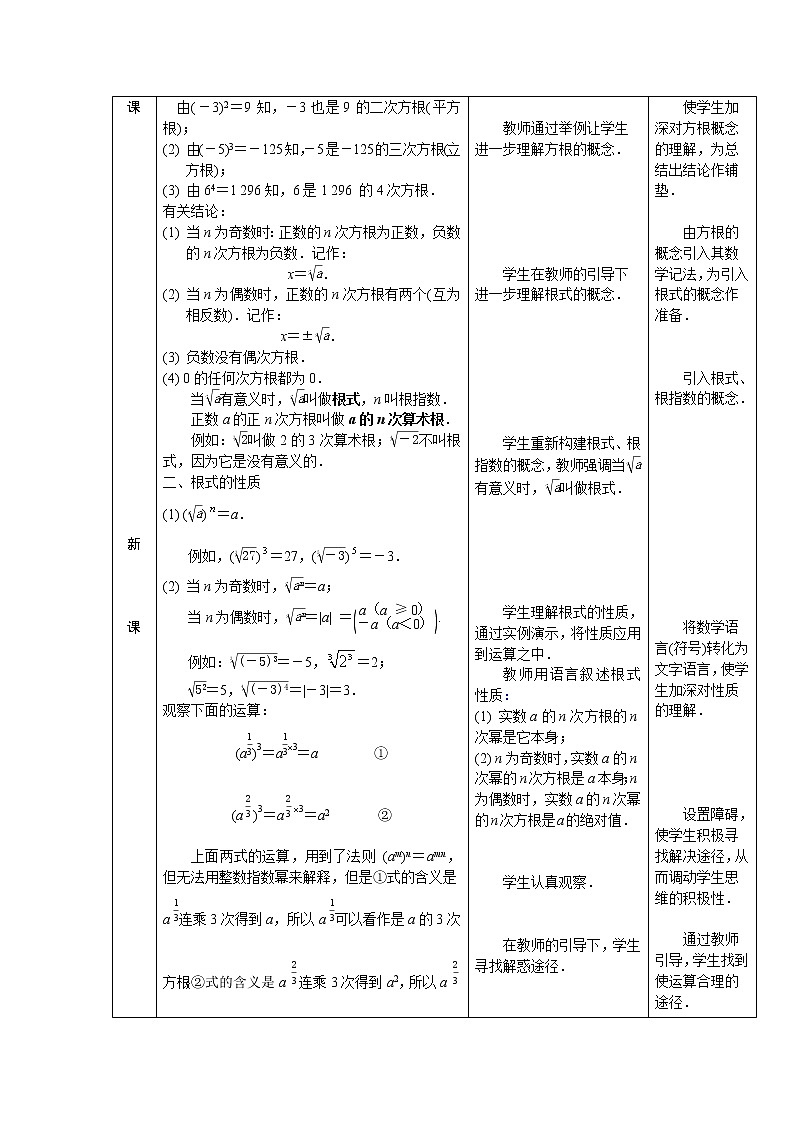
二、根式的性质
(1) ( EQ \R(n,a))＝a．
例如，( EQ \R(3,27))＝27，( EQ \R(5,－3))＝－3．
(2) 当n为奇数时， EQ \R(n,an)＝a；
当n为偶数时， EQ \R(n,an)＝|a| ＝ EQ \B\LC\{(\A\AL\COL(a（a≥0）,－a（a＜0）)) .
例如： EQ \R(3,(－5)3)＝－5，＝2；
EQ \R(,52)＝5， EQ \R(4,(－3)4)＝|－3|＝3．
观察下面的运算：
(aeq \s\up10(\f(1,3)))3＝aeq \s\up10(\f(1,3))3＝a ①
(aeq \s\up10(\f(2,3)))3＝aeq \s\up10(\f(2,3))3＝a2 ②
上面两式的运算，用到了法则 (am)n＝amn，但无法用整数指数幂来解释，但是①式的含义是aeq \s\up10(\f(1,3))连乘3次得到a，所以aeq \s\up10(\f(1,3))可以看作是a的3次方根；②式的含义是aeq \s\up10(\f(2,3))连乘3次得到a2，所以aeq \s\up10(\f(2,3))可以看作是a2的3次方根．
因此我们规定
aeq \s\up10(\f(1,3))＝ EQ \R(3,a)，aeq \s\up10(\f(2,3))＝ EQ \R(3,a2)，
以使运算合理．
三、分数指数幂
一般地，我们规定：
aeq \s\up10(\f(1,n))＝ EQ \R(n,a) (a＞0)；
aeq \s\up10(\f(m,n))＝ EQ \R(n,am)＝( EQ \R(n,a))m (a＞0，m，nN+，且 EQ \F(m,n) 为既约分数)．
aeq \s\up10(－\f(m,n))＝ EQ \F(1, aeq \s\up10(\f(m,n))) (a＞0，m，nN+，且 EQ \F(m,n) 为既约分数) ．
四、实数指数幂的运算法则
(1) aαaβ＝aα+β；
(2) (aα) β＝aα β；
(3) (a b) α＝a α b α．
以上aα，aβ中，a＞0，b＞0，且α，β为任意实数．
练习1
8eq \s\up10(\f(3,5))×8eq \s\up10(\f(2,5)) ＝8eq \s\up10(\f(3＋2,5))＝81＝8；
8eq \s\up10(\f(2,3))＝(8eq \s\up10(\f(1,3)))2＝22＝4；
3 EQ \R(3)× EQ \R(3,3) × EQ \R(6,3)＝3×3eq \s\up10(\f(1,2))×3eq \s\up10(\f(1,3))×3eq \s\up10(\f(1,6))＝31＋eq \s\up10(\f(1,2))＋eq \s\up10(\f(1,3))＋eq \s\up10(\f(1,6))＝32＝9；
(aeq \s\up9(\f(2,3))beq \s\up9(\f(1,4)))3＝(aeq \s\up10(\f(2,3)))3·(beq \s\up10(\f(1,4)))3＝a2beq \s\up10(\f(3,4))．
例1 利用函数型计算器计算(精确到0.001)：
(1) ； (2) 3.14－2； (3) 3.1eq \s\up10(\f(2,3))．
例2 利用函数型计算器计算函数值．
已知 f (x)＝2.71x，求 f (－3)，f (－2)，f(－1)，f (1)，f (2)，f (3) (精确到0.001)．
请同学们结合教材在小组内合作完成．
练习2
教材 P 98，练习A组 第3题，练习B组第3题．
教师板书课题．
学生理解方根概念．
教师通过举例让学生进一步理解方根的概念．
学生在教师的引导下进一步理解根式的概念．
学生重新构建根式、根指数的概念，教师强调当 EQ \R(n,a)有意义时， EQ \R(n,a)叫做根式．
学生理解根式的性质，通过实例演示，将性质应用到运算之中．
教师用语言叙述根式性质：
(1) 实数a的n次方根的n次幂是它本身；
(2) n为奇数时，实数a的n次幂的n次方根是a本身；n为偶数时，实数a的n次幂的n次方根是a的绝对值．
学生认真观察．
在教师的引导下，学生寻找解惑途径．
学生在教师的引导下，由特殊到一般，积极构建分数指数幂的概念．
师：负整数指数幂是怎么定义的？如何来定义负分数指数幂呢？
学生在教师的引导下，类比负整指数幂的定义，形成负分数指数幂的概念．
师：至此，我们把整数指数幂推广到了有理指数幂．有理指数幂还可以推广到实数指数幂．使学生形成实数指数幂的概念．
学生做练习．
教师讲解例1第(1)题的操作方法．
学生结合教材，完成例1第(2)、(3)题，学习用计算工具来求指数幂 ab 的值．
引入方根的概念为下一步引入分数指数做基础．
使学生加深对方根概念的理解，为总
结出结论作铺垫．
由方根的概念引入其数学记法，为引入根式的概念作准备．
引入根式、根指数的概念．
将数学语言(符号)转化为文字语言，使学生加深对性质的理解．
设置障碍，使学生积极寻找解决途径，从而调动学生思维的积极性．
通过教师引导，学生找到使运算合理的途径．
引入正分数指数幂的概念．
类比负整数指数幂的定义，引入负分数指数幂的概念．
将有理指数幂推广到实数指数幂，并给出实数指数幂的运算法则．
加深对有理指数幂的理解，并使学生进一步掌握指数幂的运算法则．
使学生掌握函数型计算器的使用．
使学生进一步巩固函数计算器的使用方法．
小
结
根式
分数指数幂
1．
正整指数幂
零指数幂
负整指数幂
整数指数幂
分数指数幂
有理指数幂
实数指数幂
2．
3．利用函数型计算器求 ab 的值．
学生在教师的引导下回顾本节课的主要内容，加深理解根式和分数指数幂的概念；理顺实数指数幂的推广过程；回顾计算器的使用方法．
简洁明了地概括本节课的重要知识，便于学生理解记忆．
理顺本节指数幂的推广思路，使学生思维清晰．
作
业
必做题：教材 P 98，练习 B 组第1题；
选做题：教材 P 98，练习 B 组第2题．
针对学生实际，对课后书面作业实施分层设置，安排基本练习题和选做题两层．