

2021-2022学年山西省运城市盐湖区九年级(上)期末数学试卷(含答案解析)
展开tan30∘的相反数是( )
A. −3B. −32C. −33D. −22
若二次函数y=ax2+bx−2的图象经过点(−2,0),则代数式2a−b的值为( )
A. 0B. 1C. −1D. 2
如图所示的物体的左视图是( )
A.
B.
C.
D.
若将抛物线y=2x2+1先向右平移1个单位长度,再向下平移3个单位长度,则所得抛物线的表达式为( )
A. y=2(x−1)2−2B. y=2(x+1)2−2
C. y=2(x−1)2+3D. y=2(x+1)2+3
某地新高考有一项“6选3”选课制,高中学生李鑫和张锋都已选了地理和生物,现在他们还需要从“物理、化学、政治、历史”四科中选一科参加考试.若这四科被选中的机会均等,则他们恰好一人选物理,另一人选化学的概率为( )
A. 18B. 14C. 38D. 12
对于二次函数y=−(x−1)2的图象,下列说法不正确的是( )
A. 开口向下B. 对称轴是直线x=1
C. 顶点坐标为(1,0)D. 当x<1时,y随x的增大而减小
如图,一艘轮船在小岛A的西北方向距小岛402海里的C处,沿正东方向航行一段时间后到达小岛A的北偏东60∘的B处,则该船行驶的路程为( )
A. 80海里B. 120海里
C. (40+402)海里D. (40+403)海里
关于x的方程ax2+(1−a)x−1=0,下列结论正确的是( )
A. 当a=0时,方程无实数根B. 当a=−1时,方程只有一个实数根
C. 当a=1时,有两个不相等的实数根D. 当a≠0时,方程有两个相等的实数根
如图,在3×3的网格中,A,B均为格点,以点A为圆心,AB的长为半径作弧,图中的点C是该弧与格线的交点,则tan∠BAC的值是( )
A. 12
B. 255
C. 53
D. 23
已知二次函数y=ax2+bx+c的图象的对称轴为直线x=1,其图象如图所示,现有下列结论:①abc>0;②2a+b=0;③4a−2b+c<0;④a+b≥m(am+b);⑤2c<3b.其中正确结论的个数是( )
A. 1
B. 2
C. 3
D. 4
课外活动小组测量学校旗杆的高度.如图,当太阳光线与地面成30∘角时,测得旗杆AB在地面上的影长BC为24米,那么旗杆AB的高度约是______ 米.(结果保留根号)
已知函数y=(m−1)xm2+3是关于x的一次函数,则m的值为______.
如图,菱形ABCD的对角线AC,BD相交于点O,E为DC的中点,若OE=2,则菱形的周长为______ .
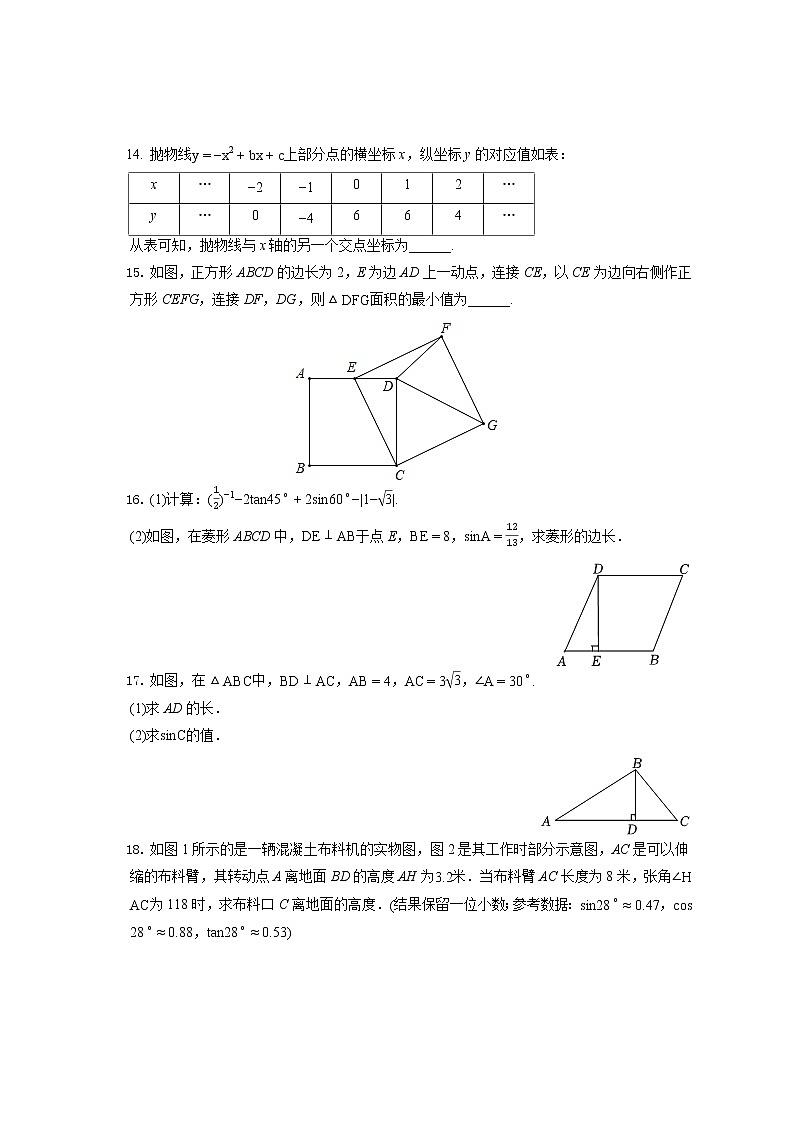
抛物线y=−x2+bx+c上部分点的横坐标x,纵坐标y的对应值如表:
从表可知,抛物线与x轴的另一个交点坐标为______.
如图,正方形ABCD的边长为2,E为边AD上一动点,连接CE,以CE为边向右侧作正方形CEFG,连接DF,DG,则△DFG面积的最小值为______.
(1)计算:(12)−1−2tan45∘+2sin60∘−|1−3|.
(2)如图,在菱形ABCD中,DE⊥AB于点E,BE=8,sinA=1213,求菱形的边长.
如图,在△ABC中,BD⊥AC,AB=4,AC=33,∠A=30∘.
(1)求AD的长.
(2)求sinC的值.
如图1所示的是一辆混凝土布料机的实物图,图2是其工作时部分示意图,AC是可以伸缩的布料臂,其转动点A离地面BD的高度AH为3.2米.当布料臂AC长度为8米,张角∠HAC为118时,求布料口C离地面的高度.(结果保留一位小数;参考数据:sin28∘≈0.47,cs28∘≈0.88,tan28∘≈0.53)
如图,一次函数y=kx+b与反比例函数y=8x(x>0)的图象交于A(m,8),B(4,n)两点,连接OA,OB.
(1)求一次函数的表达式;
(2)求△AOB的面积.
如图,在正方形ABCD中,E是BC的中点,点P在BC的延长线上,AP,DE交于点G,AP,CD交于点F.
(1)求证:AD⋅CF=CP⋅DF.
(2)若DF=2CF,AB=6,求DG的长.
某企业生产了一套健身器材,通过实体店和网上商店两种途径进行销售,销售一段时间后,该企业对这种健身器材的销售情况进行了为期30天的跟踪调查,其中实体店的日销售量y1(套)与时间x(x为整数,单位:天)的部分对应值如表:
(1)已知y1与x满足二次函数关系,求y1与x的函数关系式.
(2)网上商店的日销售量y2(套)与时间x(x为整数,单位:天)的关系如图所示,求y2与x的函数关系式并写出自变量x的取值范围.
(3)在跟踪调查的30天中,设实体店和网上商店的日销售总量为y(套),求当x为何值时,日销售总量y达到最大,并求出此时的最大值.
矩形OABC在平面直角坐标系中的位置如图所示,已知B(23,2),点A在x轴上,点C在y轴上,P是对角线OB上一动点(不与原点重合),连接PC,过点P作PD⊥PC,交x轴于点D,连接CD.
(1)当点D运动到OA的中点时,求PC2+PD2的值.
(2)在运动过程中,∠CDP的大小是否有变化?若不变,求出∠CDP的大小;若改变,请说明理由.
(3)当△ODP为等腰三角形时,直接写出点D的坐标.
已知抛物线y=−x2+bx+c交x轴于B(4,0),C(−1,0)两点,交y轴于点A,P是抛物线上一动点,设点P的横坐标为m,过点P作x轴的垂线PQ,过点A作AQ⊥PQ于点Q,连接AP(AP不平行x轴).
(1)求抛物线的表达式.
(2)如图1,若△AQP∽△AOC,求点P的坐标.
(3)如图2,若点P位于抛物线的对称轴的右侧,将△APQ沿AP对折,点Q的对应点为Q,当点Q落在x轴上时,求点P的坐标.
答案和解析
1.【答案】C
【解析】解:∵tan30∘=33,
∴tan30∘的相反数为−33.
故选:C.
利用特殊角的三角函数值得到tan30∘=33,然后根据相反数的定义求解.
本题考查了特殊角的三角函数值:熟练记住特殊角的三角函数值是解决此类问题的关键.
2.【答案】B
【解析】解:把(−2,0)代入y=ax2+bx−2得0=4a−2b−2,
∴4a−2b=2,即2a−b=1,
故选:B.
将(−2,0)代入函数解析式得4a−2b=2,进而求解.
本题考查二次图象上点的特征,解题关键是掌握二次函数与方程的关系.
3.【答案】B
【解析】解:从左面看,底层是一个圆,圆的正上方有一条线段.
故选:B.
找到从左面看所得到的图形即可,注意所有的看到的棱都应表现在左视图中.
本题考查了三视图的知识,左视图是从物体的左面看得到的视图.
4.【答案】A
【解析】解:抛物线y=2x2+1的顶点坐标为(0,1),点(0,1)向右平移1个单位长度,再向下平移3个单位长度所得对应点的坐标为(1,−2),所以新抛物线的解析式为y=2(x−1)2−2.
故选:A.
先确定出原抛物线的顶点坐标,然后根据向右平移横坐标加,向下平移纵坐标减求出新图象的顶点坐标,然后写出即可.
本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.
5.【答案】A
【解析】解:设“物理、化学、政治、历史”分别用A、B、C、D表示,
画树状图如图所示:
共有16种等可能的结果,其中李鑫和张锋恰好一人选物理,另一人选化学的结果有2种,
∴李鑫和张锋恰好一人选物理,另一人选化学的概率为216=18,
故选:A.
根据题意画出树状图,共有16种等可能的结果,其中他们恰好一人选物理,另一人选化学的结果有2种,再由概率公式求解即可.
本题考查列表法与树状图法以及概率公式,解答本题的关键是明确题意,画出相应的树状图.
6.【答案】D
【解析】解:∵二次函数y=−(x−1)2,
∴该函数图象开口向下,故选项A正确,不符合题意;
对称轴是直线x=1,故选项B正确,不符合题意;
顶点坐标为(1,0),故选项C正确,不符合题意;
当x<1时,y随x的增大而增大,故选项D错误,符合题意;
故选:D.
根据题目中的函数解析式和二次函数的性质,可以判断各个选项中的说法是否正确,从而可以解答本题.
本题考查二次函数的性质、二次函数的图象,解答本题的关键是明确题意,利用二次函数的性质解答.
7.【答案】D
【解析】解:如图,过点A作AD⊥BC于D,
由题意得,∠CAD=45∘,∠BAD=60∘,AC=402海里,
在Rt△ADC中,∠ADC=90∘,∠CAD=45∘,AC=402海里,
∴AD=CD=22×402=40(海里),
在Rt△ADB中,∠ADB=90∘,∠BAD=45∘,AD=40海里,
∴BD=3AD=403(海里),
∴BC=CD+BD=(40+403)海里,
故选:D.
通过作垂线,构造直角三角形,在两个直角三角形中,利用直角三角形的边角关系分别求出CD、BD的长,进而求出BC即可.
本题考查解直角三角形的应用,掌握直角三角形的边角关系是解决问题的前提,作垂线构造直角三角形是正确解答的关键.
8.【答案】C
【解析】解:A、当a=0时,方程为x−1=0,
解得x=1,
故当a=0时,方程有一个实数根;不符合题意;
B、当a=−1时,关于x的方程为−x2+2x−1=0,
∵△=4−4=0,
∴当a=−1时,方程有两个相等的实数根,故不符合题意;
C、当a=1时,关于x的方程x2−1=0,
故当a=1时,有两个不相等的实数根,符合题意;
D、当a≠0时,△=(1−a)2+4a=(1+a)2≥0,
∴当a≠0时,方程有相等的实数根,故不符合题意,
故选:C.
直接利用方程解的定义根的判别式分析求出即可.
此题主要考查了一元二次方程的定义,根的判别式,正确把握其定义是解题关键.
9.【答案】B
【解析】解:如图,作CH⊥AB于H.
在Rt△ACH中,∠AHC=90∘,CH=2,AC=AB=3,
∴AH=AC2−CH2=5,
∴tan∠BAC=CHAH=25=255,
故选:B.
作CH⊥AB于H.在Rt△ACH中,先利用勾股定理求出AH,再根据正切函数定义即可求出的tan∠BAC的值.
本题考查解直角三角形、勾股定理、锐角三角函数等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.
10.【答案】D
【解析】解:∵抛物线开口向下,
∴a<0,
∵抛物线对称轴为直线x=−b2a=1,
∴b=−2a>0,
∵抛物线与y轴交点在x轴上方,
∴c>0,
∴abc<0,①错误,
∴b+2a=0,②正确.
∵x=−2时,y<0,
∴4a−2b+c<0,③正确.
∵当x=1时,y取最大值,
∴a+b+c≥ax2+bx+c,
令x=m,则a+b+c≥am2+bm+c,即a+b≥m(am+b),
∴④正确.
∵x=−1时y<0,抛物线对称轴为直线x=1,
∴x=3时,y<0,
∴9a+3b+c<0,
∵−b2a=1,
∴a=−b2,
∴−92b+3b+c<0,即−32b+c<0,
∴3b>2c,⑤正确.
故选:D.
根据图象可得a,b,c符号,根据对称轴为直线x=−b2a=1可得b+2a=0,从而判断①②,根据x=−2时y<0可判断③,由x=1时y取最大值可得a+b+c≥am2+bm+c,从而判断④,由抛物线对称性可得x=3时,y<0,即9a+3b+c<0,由−b2a=1可得a=−b2,从而判断⑤.
本题考查二次函数图象与系数的关系,解题关键是掌握二次函数的性质,掌握二次函数与方程及不等式的关系.
11.【答案】83
【解析】解:由题意可得出:
tan30∘=ABBC,
则AB=BCtan30∘=24×33=83(m),
故答案为:83.
直接利用锐角三角函数关系得出tan30∘=ABBC,求出即可.
此题主要考查了解直角三角形的应用,正确选择锐角三角函数关系是解题关键.
12.【答案】−1
【解析】解:根据题意知m2=1且m−1≠0,
解得m=−1,
故答案为:−1.
根据一次函数的概念求解可得.
本题主要考查一次函数的定义,形如y=kx+b(k≠0,k、b是常数)的函数,叫做一次函数
13.【答案】16
【解析】
【分析】
本题考查了菱形的性质、直角三角形斜边上中线的性质以及三角形中位线定理的运用,本题解法多样,关键是掌握:菱形的四条边都相等;菱形的两条对角线互相垂直平分.
解法一:根据OE是△BCD的中位线,即可得到BC的长,然后根据菱形的周长公式计算即可得解.
解法二:根据根据OE是Rt△COD斜边上的中线,即可得到CD的长,然后根据菱形的周长公式计算即可得解.
【解答】
解法一:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,BO=DO,
又∵点E是CD的中点,
∴OE是△BCD的中位线,
∴BC=2OE=2×2=4,
∴菱形ABCD的周长=4×4=16.
解法二:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥BD,
又∵点E是CD的中点,
∴OE是Rt△COD斜边上的中线,
∴CD=2OE=2×2=4,
∴菱形ABCD的周长=4×4=16.
故答案为:16.
14.【答案】(3,0)
【解析】解:∵抛物线经过点(0,6),(1,6),
∴抛物线的对称轴是x=12,
∵抛物线经过点(−2,0),
∴抛物线与x轴的另一个交点坐标为(3,0).
故答案为:(3,0).
求出抛物线的对称轴为x=12,则可得出答案.
本题考查了二次函数的性质,二次函数图象上点的坐标特征,抛物线与x轴的交点.
15.【答案】32
【解析】解:设DE=x,则CE=22+x2,
∵S△DEC+S△DFG=12S正方形ECGF,
∴S△DFG=12(x2+4)−12×2x=12x2−x+2=12(x−1)2+32,
∴当x=1时,△DFG面积的最小值为32.
故答案为:32.
设DE=x,则CE=22+x2,由S△DEC+S△DFG=12S正方形ECGF可得S△DFG=12(x−1)2+32,进而求解.
本题考查与正方形有关的计算,解题关键是掌握正方形的性质,二次函数求最值的方法.
16.【答案】解:(1)原式=2−2+3−(3−1)
=3−2;
(2)∵四边形ABCD是菱形,
∴AB=BC=CD=AD,
∵DE⊥AB,sinADEAD=1213,
∴设DE=12k,AD=13k,
则AE=AD2−DE2=(13k)2−(12k)2=5k,
∴EB=13k−5k=8k=8,
∴k=1,AD=13,
∴菱形的边长为13.
【解析】(1)利用负整数指数幂及特殊角的函数值计算后即可确定正确的答案;
(2)由sinA=DEAD=1213,设DE=12k,AD=13k,则AE=5k,根据EB=13k−5k=8k=8,得到k=1,AD=13,由此即可解决问题.
考查了菱形的性质及实数的运算,解题的关键是了解菱形的四边相等,注意解题的方法.
17.【答案】解:(1)在Rt△ABD中,∠ADB=90∘,AB=4,∠A=30∘,
∴BD=12AB=2,AD=3BD=23;
(2)∵AC=33,AD=23,
∴CD=AC−AD=3.
在Rt△CBD中,∠CDB=90∘,BD=2,CD=3,
∴BC=BD2+CD2=7,
sinC=BDBC=27=277.
【解析】(1)在Rt△ABD中,根据含30∘角的直角三角形的性质得出BD=12AB=2,AD=3BD=23;
(2)先求出CD=AC−AD=3,然后在Rt△CBD中,利用勾股定理求出BC=BD2+CD2=7,最后根据三角函数的定义即可求出sinC的值.
本题考查了解直角三角形,勾股定理,锐角三角函数的定义,掌握含30∘角的直角三角形的三边关系可使计算简便.
18.【答案】解:过点C作CE⊥BD于点E,过点A作AF⊥CE于点F,
∴四边形AHEF为矩形,
∴EF=AH=3.2米,∠HAF=90∘,
∴∠CAF=∠CAH−∠HAF=118∘−90∘=28∘,
在Rt△ACF中,sin∠CAF=CFAC,
∴CF=8×sin28∘≈8×0.47=3.76(米),
∴CE=CF+EF=3.76+3.2≈7.0(米),
答:布料口C离地面的高度为7.0米.
【解析】过点C作CE⊥BD于点E,过点A作AF⊥CE于点F,求出∠CAF=28∘,利用三角函数求出CF,根据CE=CF+EF求出CE即可.
本题主要考查解直角三角形的知识,熟练利用三角函数解直角三角形是解题的关键.
19.【答案】解:(1)∵反比例函数y=8x(x>0)的图象经过A(m,8),B(4,n)两点,
∴8m=8,4n=8,
解得m=1,n=2,
∴A(1,8),B(4,2),
代入一次函数y=kx+b,可得k+b=84k+b=2,解得k=−2b=10,
∴一次函数的解析式为y=−2x+10;
(2)如图,在y=−2x+10中,令y=0,则x=5,即D(5,0),
∴OD=5,
∴△AOB的面积=△AOD的面积−△BOD的面积
=12×5×8−12×5×2
=15.
【解析】(1)依据反比例函数y=8x(x>0)的图象经过A(m,8),B(4,n)两点,即可得到m=1,n=2,把A(1,8),B(4,2),代入一次函数y=kx+b,可得一次函数的解析式为y=−2x+10;
(2)依据D(5,0),可得OD=5,再根据△AOB的面积=△AOD的面积−△BOD的面积,进行计算即可得到结论.
本题主要考查直线和双曲线交点的问题,熟练掌握待定系数法求函数解析式、反比例函数图象上点的坐标特征、割补法求三角形的面积是解题的关键.
20.【答案】(1)证明:在正方形ABCD中,有AD//BP,
△ADF∽△PCF,
∴ADCP=DFCF,即AD⋅CF=CP⋅DF.
(2)解:由(1)知ADCP=DFCF,
∵DF=2CF,AB=6,
∴CP=3,
又∵点E是BC的中点,
∴EC=12BC=3,
∴EP=AD=6,
∵AD//EP,
∴∠ADG=∠PEG,∠DAG=∠P,
∴△PGE≌△AGD,
∴DG=GE,
∵DE=32+62=35,
∴DG=352,
故DG的长为=352.
【解析】(1)根据正方形的性质,得△ADE∽△PCF,然后由相似三角形的性质可得结论;
(2)求出PC的长,从而可得PE,再利用△PGE≌△AGD及勾股定理,即可求出DG的长.
本题是考查的是相似三角形的判定与性质,掌握其性质是解决此题的关键.
21.【答案】解:(1)根据观察可设y1=ax2+bx,将,(5,25),(10,40)代入得:25a+5b=25100a+10b=40,
解得a=−15b=6,
∴y1与x的函数关系式为:y1=−15x2+6x(0≤x≤30,且x为整数);
(2)当0≤x≤10时,设y2=kx,
∵(10,40)在其图象上,
∴10k=40,
∴k=4,
∴y2与x的函数关系式为:y2=4x,
当10≤x≤30时,设y2=mx+n,
将(10,40),(30,80)代入得10m+n=4030m+n=80,
解得m=2n=20,
∴y2与x的函数关系式为:y2=2x+20,
综上所述,y2={4x(0⩽x⩽10,且x为整数)2x+20(10
∴x=10时,y最大=80;
当10
∴x=20时,y最大=100,
∵100>80,
∴当x=20时,y最大=100(百件).
【解析】(1)根据观察可设y1=ax2+bx,将(5,25),(10,40)代入即可得到结论;
(2)当0≤x≤10时,设y2=kx,求得y2与x的函数关系式为:y2=4x,当10≤x≤30时,设y2=mx+n,将(10,40),(30,80)代入得到y2与x的函数关系式为:y2=2x+20;
(3)依题意得y=y1+y2,当0≤x≤10时,得到y最大=80;当10
22.【答案】解:(1)∵点D为OA的中点,
∴OD=12OA=3,
∵PD⊥PC,
∴∠CPD=90∘,
∴PC2+PD2=CD2=OC2+OD2=22+(3)2=7;
(2)∠CDP的大小不会变化,理由如下:
过点P作PF⊥OA于F,FP的延长线交BC于E,
∴PE⊥BC,四边形OFEC是矩形,
∴EF=OC=2,
设PE=a,则PF=EF−PE=2−a,
在Rt△BEP中,tan∠CBO=PEBE=OCBC=33,
∴BE=3PE=3a,
∴CE=BC−BE=23−3a=3(2−a),
∵PD⊥PC,
∴∠CPE+∠FPD=90∘,
∵∠CPE+∠PCE=90∘,
∴∠FPD=∠ECP,
∵∠CEP=∠PFD=90∘,
∴△CEP∽△PFD,
∴CEPF=PCPD,
∴tan∠CDP=PCPD=CEPF=3(2−a)2−a=3,
∴∠CDP=60∘;
(3)∵B(23,2),四边形OABC是矩形,
∴OA=23,AB=2,
∵tan∠AOB=ABOA=33,
∴∠AOB=30∘,
当△ODP为等腰三角形时,
Ⅰ、OD=PD,
∴∠DOP=∠DPO=30∘,
∴∠ODP=120∘,
∴∠ODC=60∘
∴OD=33OC=233,
∴D(233,0);
Ⅱ、当D在x轴的正半轴上时,OP=OD,
∴∠ODP=∠OPD=75∘,
∵∠COD=∠CPD=90∘,
∴∠OCP=105∘>90∘,故不合题意舍去;
当D在x轴的负半轴上时,OP′=OD′,如图,
∵∠AOB=30∘,
∴∠D′OP′=150∘,
∵∠CP′D′=90∘,
∴∠CP′O=105∘,
∵∠COP′=60∘,
∴∠OCP′=15∘,
∴∠BCP′=75∘,
∴∠CP′B=180∘−75∘−30∘=75∘,
∴BC=BP′=23,
∴OD′=OP′=4−23,
∴D′(23−4,0);
Ⅲ、OP=PD,
∴∠POD=∠PDO=30∘,
∴∠OCP=150∘>90∘,故不合题意舍去,
点D的坐标为(23−4,0)或(233,0).
【解析】(1)由点D为OA的中点,得到OD=12OA=3,根据勾股定理即可得到PC2+PD2=CD2=OC2+OD2=22+(3)2=7即可;
(2)过点P作PF⊥OA于F,FP的延长线交BC于E,PE=a,则PF=EF−PE=2−a,根据三角函数的定义得到BE=3PE=3a,求得CE=3(2−a),根据相似三角形的性质得到CEPF=PCPD,根据三角函数的定义得到∠PDC=60∘即可;
(3)当△ODP为等腰三角形时,Ⅰ、OD=PD,解直角三角形得到OD=33OC=233,Ⅱ、OP=OD,根据等腰三角形的性质和四边形的内角和得到∠OCP=105∘>90∘,故不合题意舍去;Ⅲ、OP=PD,根据等腰三角形的性质和四边形的内角和得到∠OCP=105∘>90∘,故不合题意舍去;于是得到当△ODP为等腰三角形时,点D的坐标为(23−4,0)或(233,0).
本题是四边形的综合题,考查了矩形的性质,勾股定理,相似三角形的判定和性质,等腰三角形的性质,构造出相似三角形表示出CP和PD是解本题的关键.
23.【答案】解:(1)将B(4,0),C(−1,0)分别代入y=−x2+bx+c得,
−16+4b+c=0−1−b+c=0,
解得:b=3c=4,
∴抛物线的表达式为:y=−x2+3x+4;
(2)当x=0时,y=4,
∴A(0,4),
∴OA=4,
∵△AQP∽△AOC,
∴AQPQ=AOCO=4,即AQ=4PQ,
∵P(m,−m2+3m+4),
∴m=4|4−(−m2+3m+4)|,即4|m2−3m|=m,
当4(m2−3m)=m时,解得m=0(舍去),或m=134,此时P(134,5116);
当4(m2−3m)−m时,解得:m=0(舍去)或m=114,此时P(114,7516),
综上所述:P(134,5116)或(114,7516);
(3)P(m,−m2+3m+4)(m>32),
如图,当点Q′落在x轴上,延长QP交x轴于点H,
则PQ=4−(−m2+3m+4)=m2−3m,
∵将△APQ沿AP对折,点Q的对应点为Q′,
∴∠AQ′P=∠AQP=90∘,AQ′=AQ=m,PQ′=PQ=m2−3m,
∵∠AQ′O=∠Q′PH,
∴△AOQ′∽△Q′HP,
∴OAQ′H=AQ′Q′P,
解得:Q′H=4m−12,
∴OQ′=m−(4m−12)=12−3m,
在Rt△AOQ′中,42+(12−3m)2=m2,
解得:m=4或5,
此时点P的坐标为(4,0)或(5,−6),
综上所述:点P的坐标为(4,0)或(5,−6).
【解析】(1)将B(4,0),C(−1,0)分别代入y=−x2+bx+c即可;
(2)由△AQP∽△AOC,得AQPQ=AOCO=4,即AQ=4PQ,则m=4|4−(−m2+3m+4)|,解绝对值方程即可;
(3)当点Q′落在x轴上,延长QP交x轴于点H,得PQ=4−(−m2+3m+4)=m2−3m,则△AOQ′∽△Q′HP,得OAQ′H=AQ′Q′P,Q′H=4m−12,则OQ′=m−(4m−12)=12−3m,再利用勾股定理解决问题.
本题是二次函数综合题,主要考查了待定系数法求函数解析式,相似三角形的判定与性质,一元二次方程等知识,运用方程思想是解题的关键.
x
…
−2
−1
0
1
2
…
y
…
0
−4
6
6
4
…
时间x(天)
0
5
10
15
20
25
30
日销售量
y1(套)
0
25
40
45
40
25
0
2023-2024学年山西省运城市盐湖区九年级(上)期中数学试卷(含解析): 这是一份2023-2024学年山西省运城市盐湖区九年级(上)期中数学试卷(含解析),共35页。试卷主要包含了填空题,解答题等内容,欢迎下载使用。
2021-2022学年山西省运城市九年级(上)期末数学试卷(含答案解析): 这是一份2021-2022学年山西省运城市九年级(上)期末数学试卷(含答案解析),共23页。试卷主要包含了其中正确的个数为,5∘≈0,【答案】D,【答案】B,【答案】C等内容,欢迎下载使用。
2021-2022学年山西省运城市盐湖区七年级(上)期末数学试卷(含答案解析): 这是一份2021-2022学年山西省运城市盐湖区七年级(上)期末数学试卷(含答案解析),共14页。试卷主要包含了…第一步,…第四步,…第五步,【答案】D,【答案】C,【答案】A等内容,欢迎下载使用。












