2021-2022学年北京市大兴区九年级（上）期末数学试卷（含答案解析）

这是一份2021-2022学年北京市大兴区九年级（上）期末数学试卷（含答案解析），共21页。试卷主要包含了【答案】A，【答案】B，【答案】D，【答案】C，【答案】x1=0，x2=3等内容，欢迎下载使用。

下列图形中，既是中心对称图形也是轴对称图形的是( )
A. 圆B. 平行四边形C. 直角三角形D. 等边三角形
抛物线y=(x+1)2+2的顶点坐标是( )
A. (1,2)B. (1,−2)C. (−1,2)D. (−1,−2)
以下事件为随机事件的是( )
A. 通常加热到100℃时，水沸腾B. 篮球队员在罚球线上投篮一次，未投中
C. 任意画一个三角形，其内角和是360∘D. 半径为2的圆的周长是4π
如图，△ABC中，∠ABC=50∘，∠ACB=74∘，点O是△ABC的内心．则∠BOC等于( )
A. 124∘
B. 118∘
C. 112∘
D. 62∘
下列所给方程中，没有实数根的是( )
A. x2+2x=0B. 5x2−4x−2=0
C. 3x2−4x+1=0D. 4x2−3x+2=0
将二次函数y=x2−4x+5化为y=x−h2+k的形式，结果为( )
A. y=x−22+1B. y=x+22+1C. y=x−42+1D. y=x+42+1
如图，⊙C与∠AOB的两边分别相切，其中OA边与⊙C相切于点P ，若∠AOB=90∘，OP=4，则OC的长为( )
A. 8B. 162C. 42D. 22
小亮、小明、小刚三名同学中，小亮的年龄比小明的年龄小2岁，小刚的年龄比小明的年龄大1岁，并且小亮与小刚的年龄的乘积是130.你知道这三名同学的年龄各是多少岁吗？设小明的年龄为x岁，则可列方程为( )
A. (x+2)(x−1)=130B. (x−2)(x+1)=130
C. x(x−2)=130D. x(x+1)=130
一元二次方程x2−3x=0的根是__________.
如图，A，B，C是⊙O上的三个点，若∠AOB=70∘，则∠C=__________.
已知抛物线y=x2−x−3经过点A(2,y1)、B(3,y2)，则y1与y2的大小关系是__________.
如图，将△AOB绕点O按逆时针方向旋转45∘后得到△A′OB′，若∠AOB=15∘，则∠AOB′的度数是__________.
圆心角是270∘的扇形的半径为4cm，则这个扇形的面积是__________cm2.
请写出一个开口向上，并且对称轴为直线x=1的抛物线的表达式y=__________.
若一个扇形的半径是18cm，且它的弧长是6πcm，则此扇形的圆心角等于__________.
已知点A的坐标为(a,b)，O为坐标原点，连接OA，将线段OA绕点O顺时针旋转90∘得到线段OA1，则点A1的坐标为 −−−−.
计算：27+(3−π)0+|1−3|+3×13.
在平面直角坐标系xOy中，二次函数y=x2−2mx+5m的图象经过点(1,−2).
(1)求二次函数的表达式；
(2)求二次函数图象的对称轴．
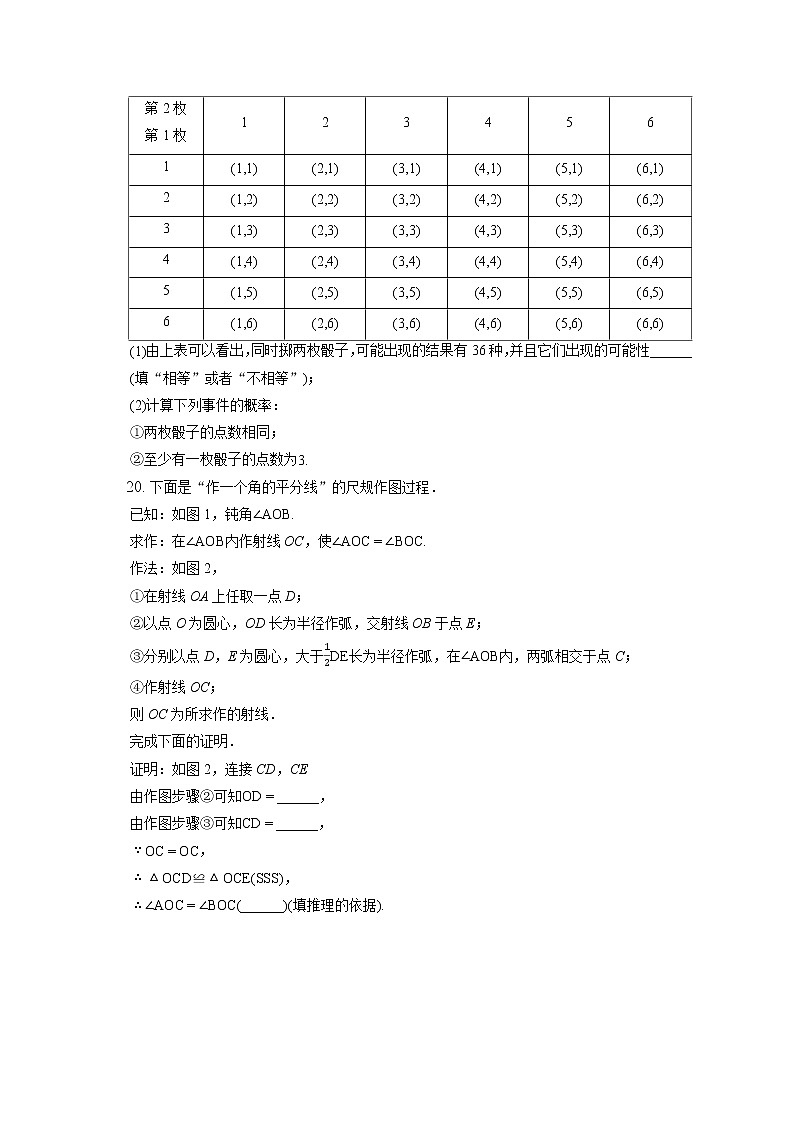
同时掷两枚质地均匀的骰子，两枚骰子分别记为第1枚和第2枚，下表列举出了所有可能出现的结果．
(1)由上表可以看出，同时掷两枚骰子，可能出现的结果有36种，并且它们出现的可能性______(填“相等”或者“不相等”)；
(2)计算下列事件的概率：
①两枚骰子的点数相同；
②至少有一枚骰子的点数为3.
下面是“作一个角的平分线”的尺规作图过程．
已知：如图1，钝角∠AOB.
求作：在∠AOB内作射线OC，使∠AOC=∠BOC.
作法：如图2，
①在射线OA上任取一点D；
②以点O为圆心，OD长为半径作弧，交射线OB于点E；
③分别以点D，E为圆心，大于12DE长为半径作弧，在∠AOB内，两弧相交于点C；
④作射线OC；
则OC为所求作的射线．
完成下面的证明．
证明：如图2，连接CD，CE
由作图步骤②可知OD=______，
由作图步骤③可知CD=______，
∵OC=OC，
∴△OCD≌△OCE(SSS)，
∴∠AOC=∠BOC(______)(填推理的依据).
如图，AB是⊙O的直径，CD是⊙O的一条弦，且CD⊥AB于点E.
(1)求证：∠BCO=∠D；
(2)若CD=42，OE=1，求⊙O的半径．
已知关于x的一元二次方程x2−3x+2a−1=0有两个不相等的实数根．
(1)求a的取值范围；
(2)若a为正整数，求方程的根．
某超市按每袋20元的价格购进某种软糖，在销售过程中发现，该种软糖每天的销售量w(袋)与销售单价x(元)满足w=−2x+80(20≤x≤40)，如果销售这种软糖每天的利润为y(元).
(1)求y与x之间的函数关系式；
(2)当软糖销售单价定为每袋多少元时，销售这种软糖每天的利润最大？最大利润是多少？
在平面直角坐标系xOy中，抛物线y=x2−4x−1与y轴交于点A，其对称轴与x轴交于点B，一次函数y=kx+b(k≠0)的图象经过点A，B.
(1)求一次函数的表达式；
(2)当x>−3时，对于x的每一个值，函数y=nx(n≠0)的值大于一次函数y=kx+b的值，直接写出n的取值范围．
已知：如图，在△ABC中，AB=AC，D是BC的中点．以BD为直径作⊙O，交边AB于点P，连接PC，交AD于点E.
(1)求证：AD是⊙O的切线；
(2)若PC是⊙O的切线，BC=8，求PC的长．
在平面直角坐标系xOy中，二次函数y=x2+bx+c的图象经过点(0,−3)，(3,0).
(1)求二次函数的表达式；
(2)将二次函数y=x2+bx+c的图象向上平移n(n>0)个单位后得到的图象记为G，当0≤x≤52时，图象G与x轴只有一个公共点，结合函数的图象，直接写出n的取值范围．
如图，在等腰△ABC中，∠BAC=90∘，点D在线段BC的延长线上，连接AD，将线段AD绕点A逆时针旋转90∘得到线段AE，连接CE，射线BA与CE相交于点F.
(1)依题意补全图形；
(2)用等式表示线段BD与CE的数量关系，并证明；
(3)若F为CE中点，AB=2，则CE的长为______.
在平面直角坐标系xOy中，点M在x轴上，以点M为圆心的圆与x轴交于A(1,0)，B(4,0)两点，对于点P和⊙M，给出如下定义：若抛物线y=ax2+bx+c(a≠0)经过A，B两点且顶点为P，则称点P为⊙M的“图象关联点”．
(1)已知E(5,2)，F(52,−4)，G(3,1)，H(52,3)，在点E，F，G，H中，⊙M的”图象关联点”是______；
(2)已知⊙M的“图象关联点”P在第一象限，若OP=53PM，判断OP与⊙M的位置关系，并证明；
(3)已知C(4,2)，D(1,2)，当⊙M的“图象关联点”P在⊙M外且在四边形ABCD内时，直接写出抛物线y=ax2+bx+c中a的取值范围．
答案和解析
1.【答案】A
【解析】解：A.圆既是中心对称图形，也是轴对称图形，故此选项符合题意；
B.平行四边形是中心对称图形，不是轴对称图形，故此选项不合题意；
C.直角三角形不是中心对称图形，也不一定是轴对称图形，故此选项不合题意；
D.等边三角形是轴对称图形，不是中心对称图形，故此选项不合题意．
故选：A.
根据轴对称图形与中心对称图形的概念求解．
本题考查中心对称图形和轴对称图形的概念，关键是掌握好中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合，中心对称图形是要寻找对称中心，图形绕对称中心旋转180∘后与原图形重合．
2.【答案】C
【解析】解：∵y=(x+1)2+2为二次函数的顶点式，
∴该抛物线的顶点坐标为(−1,2)，
故选：C.
根据抛物线的顶点式直接得出顶点坐标即可．
本题主要考查二次函数的性质，关键是要能根据顶点式直接写出顶点的坐标．
3.【答案】B
【解析】解：A.通常加热到100℃时，水沸腾，这是必然事件，故A不符合题意；
B.篮球队员在罚球线上投篮一次，未投中，这是随机事件，故B符合题意；
C.任意画一个三角形，其内角和是360∘，这是不可能事件，故C不符合题意；
D.半径为2的圆的周长是4π，这是必然事件，故D不符合题意；
故选：B.
根据必然事件，随机事件，不可能事件的特点判断即可．
本题考查了随机事件，熟练掌握必然事件，随机事件，不可能事件的特点是解题的关键．
4.【答案】B
【解析】解：∵点O是△ABC的内心，
∴OB平分∠ABC，OC平分∠ACB，
∴∠OBC=12∠ABC=12×50∘=25∘，
∠OCB=12∠ACB=12×74∘=37∘，
∴∠BOC=180∘−∠OBC−∠OCB=180∘−25∘−37∘=118∘.
故选：B.
根据三角形内心的性质得到∠OBC=12∠ABC=25∘，∠OCB=12∠ACB=37∘，然后根据三角形内角和计算∠BOC的度数．
本题考查了三角形的内切圆与内心：三角形的内心就是三角形三个内角角平分线的交点，三角形的内心与三角形顶点的连线平分这个内角．
5.【答案】D
【解析】解：A.x2+2x=0，
∵b2−4ac=4>0，
∴方程有实数根，故本选项不符合题意；
B.5x2−4x−2=0，
∵b2−4ac=16+40=56>0，
∴方程有实数根，故本选项不符合题意；
C.3x2−4x+1=0，
∵b2−4ac=16−12=4>0，
∴方程有实数根，故本选项不符合题意；
D.4x2−3x+2=0，
∵b2−4ac=9−32=−23<0，
∴方程没有实数根，故本选项符合题意；
故选：D.
求出各选项一元二次方程根的判别式的值，判断出正负即可确定一元二次方程是否有实数根．
本题主要考查了根的判别式，熟记“当Δ<0时，一元二次方程没有实数根”是解本题的关键．
6.【答案】A
【解析】解：y=x2−4x+5=x−22+1，
故选：A.
利用配方法把二次函数的一般形式配成二次函数的顶点式．
本题考查了二次函数的三种形式，二次函数的解析式有三种形式：
(1)一般式：y=ax2+bx+c(a≠0,a、b、c为常数)；
(2)顶点式：y=ax−h2+k；(a≠0,a、h、k为常数)
(3)交点式(函数图象与x轴交点的横坐标为x1,x2)：y=ax−x1x−x2.(a≠0,a、x1、x2为常数)
7.【答案】C
【解析】解：如图，连接CP，
∵OA边与⊙C相切于点P，
∴CP⊥OA，
∴∠OPC=90∘，
∵⊙C与∠AOB的两边分别相切，∠AOB=90∘，
∴OC平分∠AOB，
∴∠COP=12∠AOB=12×90∘=45∘，
∴△OCP为等腰直角三角形，
∵OP=4，
∴OC=2OP=42.
故选：C.
如图，连接CP，先利用切线的性质得到∠OPC=90∘，再利用切线长定理得到OC平分∠AOB，则△OCP为等腰直角三角形，从而得到OC=2OP.
本题考查了切线的性质：圆的切线垂直于经过切点的半径．也考查了切线长定理．
8.【答案】B
【解析】解：∵小明的年龄为x岁，
小亮的年龄比小明的年龄小2岁，小刚的年龄比小明的年龄大1岁，
∴小亮的年龄为(x−2)岁，小刚的年龄为(x+1)岁．
依题意得：(x−2)(x+1)=130.
故选：B.
小明的年龄为x岁，由三人年龄间的关系可得出：小亮的年龄为(x−2)岁，小刚的年龄为(x+1)岁，再根据小亮与小刚的年龄的乘积是130，即可得出关于x的一元二次方程，此题得解．
本题考查了由实际问题抽象出一元二次方程，找准等量关系，正确列出一元二次方程是解题的关键．
9.【答案】x1=0，x2=3
【解析】解： x2−3x=0，
∴x(x−3)=0，
∴x=0，或x−3=0，
∴x1=0，x2=3.
故答案为x1=0，x2=3.
首先利用提取公因式法分解因式，由此即可求出方程的解．
本题主要考查了用因式分解法解一元二次方程．
10.【答案】35∘
【解析】解：∵∠AOB=70∘，
∴∠C=12∠AOB=12×70∘=35∘，
故答案为：35∘.
根据圆周角定理进行计算即可．
本题考查了圆周角定理：一条弧所对圆周角等于它所对圆心角的一半，熟练掌握圆周角定理是解题的关键．
11.【答案】y1【解析】解：∵函数y=x2−x−3的对称轴为直线x=−b2a=12，
∴A(2,y1)、B(3,y2)在对称轴右侧，
∵a=1，
∴抛物线图象开口向上，
∴对称轴右侧y随x的增大而增大，
∵2<3，
∴y1故答案为：y1先求得函数y=x2−x−3的对称轴为直线x=12，再判断A(2,y1)、B(3,y2)在对称轴右侧，利用函数图象的开口方向和增减性判断出y1与y2的大小关系．
此题主要考查了二次函数图象上点的特征和函数图象的增减性，利用已知解析式得出对称轴，进而利用二次函数图象的增减性得出答案是解题关键．
12.【答案】30∘
【解析】解：∵将△AOB绕点O按逆时针方向旋转45∘后得到△A′OB′，
∴∠A′OA=45∘，∠AOB=∠A′OB′=15∘，
∴∠AOB′=∠A′OA−∠A′OB′
=45∘−15∘
=30∘，
故答案是：30∘.
根据旋转的性质：旋转前后图形全等以及对应边的夹角等于旋转角，进而得出答案即可．
此题主要考查了旋转的性质，根据旋转的性质得出∠A′OA=45∘，∠AOB=∠A′OB′=15∘是解题关键．
13.【答案】12π
【解析】解：∵扇形的圆心角为270∘，半径为4cm，
∴这个扇形的面积S=270π×42360=12π(cm2)，
故答案为：12π.
根据扇形的面积公式求出答案即可．
本题考查了扇形的面积计算，能熟记扇形的面积公式是解此题的关键，
注意：圆心角为n∘，半径为r的扇形的面积S=nπr2360.
14.【答案】(x−1)2(答案不唯一)
【解析】解：由题意可设y=a(x−h)2+k，
∵抛物线的开口向上，并且对称轴为直线x=1，
∴a>0，h=1，
可令a=1，k=0，
符合的表达式是y=(x−1)2，
故答案为：(x−1)2(答案不唯一).
此题是一道开放型的题目，答案不唯一，只要写出一个符合的即可．
本题考查了用顶点式求二次函数的解析式和二次函数的性质，能熟记二次函数中顶点式的性质是解此题的关键．
15.【答案】60∘
【解析】解：设此扇形的圆心角为n∘.
由题意得6π=nπ×18180，
解得n=60，
故答案为：60∘.
利用弧长公式求解即可．
本题考查的是弧长公式的应用，掌握弧长的公式l=nπr180(其中扇形圆心角是n∘，半径是r)是解题的关键．
16.【答案】(b,−a)
【解析】解：如图，不妨假设A在第一象限，过点A作AB⊥y轴于B，过点A1作A1B1⊥x轴于B1.
∵A(a,b)，
∴AB=a，OB=b，
∵线段OA绕点O顺时针旋转90∘得到线段OA1，
∴∠AOA1=∠BOB1=90∘，
∴∠AOB=∠A1OB1，且OA=OA1，∠ABO=∠A1B1O=90∘，
∴∠ABO=∠A1B1O∠AOB=∠A1OB1OA=OA1
∴△OAB≌△OA1B1(AAS)，
∴OB1=OB=b，A1B1=AB=a，
∴A1(b,−a).
故答案为：(b,−a).
如图，不妨假设A在第一象限，过点A作AB⊥y轴于B，过点A1作A1B1⊥x轴于B1.构造全等三角形解决问题即可．
本题考查旋转变换，全等三角形的判定和性质等知识，解题的关键是画出图形添加常用辅助线，构造全等三角形来解决问题．
17.【答案】解：27+(3−π)0+|1−3|+3×13
=33+1+3−1+3
=53.
【解析】先根据二次根式的化简，零指数幂，绝对值的非负性质以及分母有理化将各式化简，然后再进行计算即可．
本题考查了实数的运算，准确熟练地化简各式是解题的关键．
18.【答案】解：(1)∵二次函数y=x2−2mx+5m的图象经过点(1,−2)，
∴把点1,−2代入二次函数y=x2−2mx+5m，得−2=1−2m+5m，
解得：m=−1.
∴二次函数的表达式为y=x2+2x−5；
(2)在二次函数y=x2+2x−5中，
∵a=1，b=2，
∴−b2a=−22×1=−1，
∴二次函数图象的对称轴为直线x=−1.
【解析】本题考查了待定系数法求二次函数解析式，二次函数的图象与性质，二次函数图象上点的坐标特征，准确熟练地进行计算是解题的关键．
(1)把点(1,−2)代入函数关系式进行计算即可；
(2)根据对称轴公式进行计算即可．
19.【答案】解：(1)相等；
(2)①由表可知，共有36种等可能的结果，两枚骰子的点数相同(记为事件A)的结果有6种，
即(1,1)，(2,2)，(3,3)，(4,4)，(5,5)，(6,6)，
∴P(A)=636=16；
②共有36种等可能的结果，至少有一枚骰子的点数为3(记为事件B)的结果有11种，
∴P(B)=1136.
【解析】
此题考查的是用列表法求概率．列表法可以不重复不遗漏地列出所有可能的结果，适合于两步完成的事件；解题时要注意此题是放回试验还是不放回试验．用到的知识点为：概率=所求情况数与总情况数之比．
【分析】
(1)由随机事件的定义即可得出结论；
【解答】
解：由表可以看出，同时掷两枚骰子，可能出现的结果有36种，并且它们出现的可能性相等，
故答案为：相等；
(2)①由表可知，共有36种等可能的结果，两枚骰子的点数相同(记为事件A)的结果有6种，再由概率公式求解即可；
②共有36种等可能的结果，至少有一枚骰子的点数为3(记为事件B)的结果有11种，再由概率公式求解即可．
20.【答案】OE；CE；全等三角形的对应角相等．
【解析】根据作图过程即可完成证明．
本题考查了作图-复杂作图，全等三角形的判定与性质，角平分线的定义，解决本题的关键是掌握基本作图方法．
证明：如图2，连接CD，CE，
由作图步骤②可知OD=OE，
由作图步骤③可知CD=CE，
∵OC=OC，
∴△OCD≌△OCE(SSS)，
∴∠AOC=∠BOC(全等三角形的对应角相等).
故答案为：OE;CE;全等三角形的对应角相等．
21.【答案】(1)证明：∵OC=OB，
∴∠BCO=∠B，
∵AC=AC，
∴∠B=∠D，
∴∠BCO=∠D；
(2)解：∵AB是⊙O的直径，且CD⊥AB于点E，
∴CE=12CD，
∵CD=42，
∴CE=12×42=22，
在Rt△OCE中，OC2=CE2+OE2，
∵OE=1，
∴OC2=(22)2+12，
解得：OC=±3(负数舍去)，
∴OC=3，
∴⊙O的半径为3.
【解析】(1)根据等腰三角形性质求出∠BCO=∠B，根据圆周角定理得出∠B=∠D，即可得证；
(2)根据垂径定理求出CE=12CD=22，再根据勾股定理求出OC即可．
本题考查了垂径定理，勾股定理，等腰三角形的性质，圆周角定理等知识点，能求出CE=12CD和∠B=∠D是解此题的关键．
22.【答案】解：(1)∵关于x的一元二次方程x2−3x+2a−1=0有两个不相等的实数根，
∴Δ =(−3)2−4(2a−1)>0，
解得：a<138，
∴a的取值范围为a<138；
(2)∵a<138，且a为正整数，
∴a=1.
此时，方程为x2−3x+1=0，
解得：x1=3+52，x2=3−52，
∴方程的根为x1=3+52，x2=3−52.
【解析】本题主要考查了根的判别式以及解一元二次方程，解题的关键是：(1)熟记“当Δ>0时，方程有两个不相等的实数根”；(2)熟练掌握一元二次的解法-公式法．
(1)根据方程根的判别式Δ>0，即可得出关于a的一元一次不等式，解之即可得出a的取值范围；
(2)由(1)可求得a的正整数值，代入原方程，解之即可求出方程的根．
23.【答案】解：(1)由题意得：y=w(x−20)=(−2x+80)(x−20)=−2x2+120x−1600，
故函数关系式为y=−2x2+120x−1600；
(2)y=−2x2+120x−1600=−2(x−30)2+200，
∵20≤x≤40，a=−2<0，
∴当x=30时，y最大值=200.
答：当软糖销售单价定为每袋30元时，销售这种软糖每天的利润最大，最大利润为200元．
【解析】本题考查的是二次函数的应用，根据题意得出二次函数解析式是解题关键．
(1)用每袋软糖的利润乘以销售量得到每天的利润；
(2)由(1)得到的是一个二次函数，利用二次函数的性质，可以求出最大利润以及销售单价．
24.【答案】解：(1)∵抛物线y=x2−4x−1与y轴交于点A，
令x=0时，y=−1，
∴点A坐标为(0,−1).
∵抛物线的对称轴为直线x=−−42=2，
∴对称轴与x轴的交点B的坐标为(2,0).
∵一次函数y=kx+b过A(0,−1)，B(2,0)，
∴b=−10=2k+b，
解得：b=−1k=12，
∴一次函数的表达式为y=12x−1；
(2)12≤n≤56.
【解析】本题考查待定系数法解一次函数解析式及一次函数和不等式的关系，解题关键是熟练掌握一次函数的性质．
(1)由抛物线y=x2−4x−1求得A、B的坐标，然后根据待定系数法求一次函数解析式；
(2)求得x=−3时，函数y=12x−1的对应值，代入y=nx求得n的值，观察图象即可求得n的取值范围．
解：如图，
把x=−3代入y=12x−1得，y=−52，
把点(−3,−52)代入y=nx(n≠0)得，−52=−3n，
∴n=56，
由图象可知，当x>−3时，对于x的每一个值，函数y=nx(n≠0)的值大于一次函数y=kx+b的值，则n的取值范围是12≤n≤56.
故答案为：12≤n≤56.
25.【答案】(1)证明：∵AB=AC，D是BC的中点，
∴AD⊥BC，
∵BD是⊙O的直径，
∴AD是⊙O的切线；
(2)解：连接OP，
∵PC是⊙O的切线，
∴∠OPC=90∘，
∵BC=8，D是BC的中点，
∴BD=CD=12BC=4，
∵BD是⊙O的直径，
∴OD=OP=2，
∴OC=OD+CD=6，
Rt△PCO中
∴PC=OC2−OP2=62−22=42.
【解析】本题考查了切线的判定与性质，等腰三角形的性质，熟练掌握切线的判定与性质是解题的关键．
(1)要证明AD是⊙O的切线，只要证明BD⊥AD即可，根据题目的已知，利用等腰三角形的三线合一性质进行解答即可；
(2)根据已知PC是⊙O的切线，想到连接OP，可得OP⊥PC，先利用D是BC的中点，求出BD和CD的长，进而求出圆的半径，最后在Rt△OPC中进行计算即可．
26.【答案】解：(1)∵二次函数y=x2+bx+c的图象经过点(0,−3)，(3,0)，
∴c=−39+3b+c=0，解得：b=−2c=−3，
∴二次函数的表达式为y=x2−2x−3.
(2)74≤n<3或n=4.
【解析】本题考查了二次函数的解析式求解、二次函数的增减性，解题的关键是会作出对应的函数图象．
(1)先代入点(0,−3)，(3,0)求得b和c的值，然后得到二次函数的表达式；
(2)先作出对应的函数图象，然后得到n的取值范围．
解：∵y=x2−2x−3=x−12−4，且向上平移n个单位，
∴图象G的函数解析式为y=x−12+n−4，
如图1，当平移后的图象的顶点在x轴上时，
∵当0≤x≤52，图象G与x轴只有一个公共点，
∴n−4=0，
∴n=4；
如图2，当x=0时，y=n−3，当x=52时，y=n−74，
∵当0≤x≤52，图象G与x轴只有一个公共点，
∴n−3<0≤n−74，
解得：74≤n<3，
综上所述，n的取值范围为74≤n<3或n=4.
27.【答案】解：(1)依题意补全图形如下：
(2)线段BD与CE的数量关系是：BD=CE，
证明：在等腰△ABC中，∠BAC=90∘，
∴AB=AC，
∵AD绕点A逆时针旋转90∘得到AE，
∴AD=AE，∠DAE=90∘，
∴∠BAC=∠DAE=90∘，
∴∠BAC+∠CAD=∠DAE+∠CAD，
∴∠BAD=∠CAE，
∴△ABD≌△ACE(SAS)，
∴BD=CE；
(3)4.
【解析】
此题是几何变换综合题，主要考查了旋转的性质，全等三角形的判定和性质，等腰直角三角形的性质，勾股定理，判断出△ABD≌△ACE是解本题的关键．
【分析】
(1)利用旋转画出AE，连接CE，即可得出图形；
(2)先判断出∠BAD=∠CAE，进而判断出△ABD≌△ACE(SAS)，即可得出结论；
(3)先求出BC，再判断出CF=BC，即可得出答案．
【解答】
解：在等腰△ABC中，∠BAC=90∘，
∴∠ABC=∠ACB=45∘，
又∵在等腰△ABC中，BC2=AB2+AC2，AB=2，AB=AC，
∴BC2=2AB2=2×22=4，
BC=2，
由(2)知，△ABD≌△ACE，
∴∠ABD=∠ACE=45∘，
∴∠BCE=90∘，
∴∠BFC=90∘−∠ABC=45∘=∠ABC，
∴CF=BC=2，
∵点F是CE的中点，
∴CE=2CF=4，
故答案为：4.
28.【答案】解：(1)F，H；
(2)OP与⊙M的位置关系是：相切．理由如下：
∵AB为⊙M的直径，
∴M为AB的中点．
∵A(1,0)，B(4,0)，
∴AM=32.
∴OM=52.
连接PM.
∵P为⊙M的“图象关联点”，
∴点P为抛物线的顶点．
∴点P在抛物线的对称轴上．
∴PM是AB的垂直平分线．
∴PM⊥AB.
过点M作MN⊥OP于N.
S△OMP=12OM⋅PM=12OP⋅MN.
∵OP=53PM，
∴MN=OM⋅PMOP=32=AM.
∴MN是⊙M的半径，且MN⊥OP.
∴OP与⊙M相切．
(3)−89【解析】
本题考查圆的综合问题，解题关键是根据“图象关联点”的定义，得出点P的横坐标；涉及待定系数法求函数解析式，三角形的面积等知识，综合程度较高，需要学生认真理解题意．
【分析】
(1)由抛物线及圆的对称性可知，⊙M的”图象关联点”在线段AB的垂直平分线上，由此可判断；
【解答】
∵抛物线y=ax2+bx+c(a≠0)经过A(1,0)，B(4,0)两点且顶点为P，
则顶点P的横坐标为52，
在点E，F，G，H中，点F和点H的横坐标为52，
∴在点E，F，G，H中，⊙M的”图象关联点”是F，H；
故答案为：F，H.
(2)连接PM，过点M作MN⊥OP于点N，证明MN=AM即可；
(3)求出点P纵坐标为1.5或2时的函数解析式，再判断a的取值范围即可．
【解答】
由(1)知，顶点P的横坐标为52，由(2)知⊙M的半径为1.5，
已知C(4,2)，D(1,2)，
当⊙M的“图象关联点”P在⊙M外且在四边形ABCD内时，
顶点P的纵坐标范围大于1.5且小于2，
当抛物线顶点坐标为(2.5,2)时，设抛物线的解析式为：y=a(x−2.5)2+2，把点A(1,0)代入得，
a=−89；
当抛物线顶点坐标为(2.5,1.5)时，设抛物线的解析式为：y=a(x−2.5)2+1.5，把点A(1,0)代入得，a=−23；
∴a的取值范围为：−89第1枚
1
2
3
4
5
6
1
(1,1)
(2,1)
(3,1)
(4,1)
(5,1)
(6,1)
2
(1,2)
(2,2)
(3,2)
(4,2)
(5,2)
(6,2)
3
(1,3)
(2,3)
(3,3)
(4,3)
(5,3)
(6,3)
4
(1,4)
(2,4)
(3,4)
(4,4)
(5,4)
(6,4)
5
(1,5)
(2,5)
(3,5)
(4,5)
(5,5)
(6,5)
6
(1,6)
(2,6)
(3,6)
(4,6)
(5,6)
(6,6)