苏教版 (2019)必修 第二册11.3 余弦定理、正弦定理的应用评课ppt课件

11.3　余弦定理、正弦定理的应用

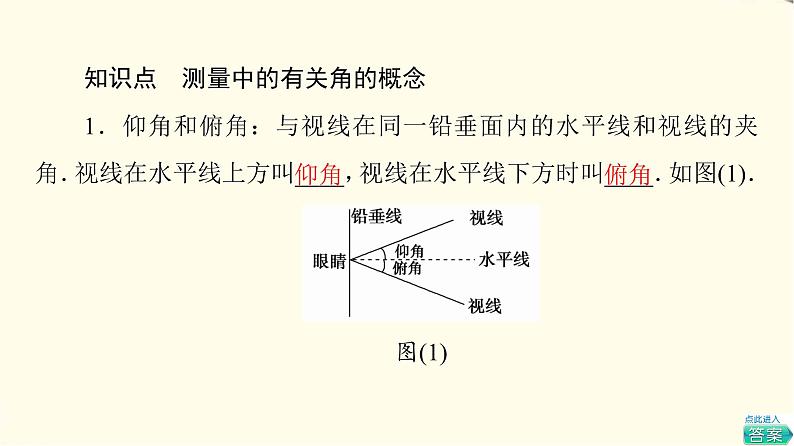
知识点　测量中的有关角的概念

1．仰角和俯角：与视线在同一铅垂面内的水平线和视线的夹角．视线在水平线上方叫仰角，视线在水平线下方时叫俯角．如图(1)．

图(1)

2．方位角：从指北方向线顺时针转到目标方向线所成的水平角，如图(2)，方向线PA，PB的位角分别为40°，240°．

图(2)　　　　　　　图(3)

3．方向角：指北或指南的方向线与目标方向线所成的小于90°的角，叫方向角，它是方位角的另一种表示形式．如图(3)，方向线OA，OB的方向角分别为北偏东60°，南偏西30°．

类型1　正、余弦定理在物理学中的应用

【例1】　如图，墙上有一个三角形灯架OAB，灯所受的重力为10 N，且OA，OB都是细杆，只受沿杆方向的力．试求杆OA，OB所受的力(结果精确到0.1)．

[解]　如图，作＝F，将F沿A到O，O到B两个方向进行分解，即作▱OCED，则＝＝F1，＝F2．由题设条件可知，||＝10，∠OCE＝50°，∠OEC＝70°，所以∠COE＝180°－50°－70°＝60°．

在△OCE中，由正弦定理，

得＝，

＝，

因此，|F1|＝≈11.3 N，

|F2|＝≈12.3 N．

即灯杆OA所受的力为11.3 N，灯杆OB所受的力为12.3 N．

在运用正弦定理、余弦定理解决力的合成与分解问题时，通常涉及平行四边形，根据题意，选择一个或几个三角形，然后通过解这些三角形，得出实际问题的解.

[跟进训练]

1．作用于同一点的三个力F1，F2，F3平衡．已知F1＝30 N，F2＝50 N，F1与F2之间的夹角是60°，求F3的大小与方向(精确到0.1°)．

[解]　F3应和F1，F2的合力F平衡，所以F3和F在同一直线上，并且大小相等，方向相反．如图，在△OF1F中，由余弦定理，得

F＝＝70(N)，

再由正弦定理，得

sin∠F1OF＝＝，

所以∠F1OF≈38.2°，

从而∠F1OF3≈141.8°．

即F3为70 N，F3和F1间的夹角为141.8°．

类型2　正、余弦定理在几何中的应用

【例2】　如图，在△ABC中，B＝，AC＝2，cos C＝．

(1)求sin∠BAC的值；

(2)设BC的中点为D，求中线AD的长．

[解]　(1)因为cos C＝，且C是三角形的内角，

所以sin C＝＝＝．

所以sin∠BAC＝sin[π－(B＋C)]＝sin(B＋C)

＝sin Bcos C＋cos Bsin C

＝×＋×＝．

(2)在△ABC中，由正弦定理得，

＝，则

BC＝×sin∠BAC＝×＝6，

所以CD＝BC＝3．

又在△ADC中，AC＝2，cos C＝，

所以由余弦定理得，

AD＝

＝＝．

三角形中几何计算问题的解题思路

(1)正确挖掘图形中的几何条件，简化运算是解题要点，善于应用正弦定理、余弦定理，只需通过解三角形，一般问题便能很快解决．

(2)此类问题突破的关键是仔细观察，发现图形中较隐蔽的几何条件．

[跟进训练]

2．如图所示，△ACD是等边三角形，△ABC是等腰直角三角形，∠ACB＝90°，BD交AC于E，AB＝2．

(1)求cos∠CBE的值；

(2)求AE．

[解]　(1)因为∠BCD＝90°＋60°＝150°，CB＝AC＝CD，所以∠CBE＝15°．

所以cos∠CBE＝cos(45°－30°)＝．

(2)在△ABE中，AB＝2，

由已知和(1)知∠ABE＝∠ABC－∠CBE＝45°－15°＝30°，

∠AEB＝∠ACB＋∠EBC＝90°＋15°＝105°，

由正弦定理，得＝，

∴AE＝＝＝－．

类型3　正、余弦定理在测量学中的应用

　测量距离问题

【例3】　某基地进行实兵对抗演习，红方为了准确分析战场形势，从相距a(km)的军事基地C和D处测得蓝方两支精锐部队分别在A处和B处，且∠ADB＝30°，∠BDC＝30°，∠DCA＝60°，∠ACB＝45°，如图所示，求蓝方这两支精锐部队间的距离．

[解]　法一：∠ADC＝∠ADB＋∠BDC＝60°．

∵∠ACD＝60°，

∴∠DAC＝60°，

∴AD＝CD＝a(km)．

在△BCD中，∠DBC＝180°－30°－105°＝45°，

由正弦定理得＝，

得BD＝CD·＝a·＝a(km)．

在△ADB中，由余弦定理得

AB2＝AD2＋BD2－2AD·BDcos∠ADB

＝a2＋－2×a×a×＝a2，

∴AB＝a(km)．

故蓝方这两支精锐部队间的距离为a(km)．

法二：在△BCD中，∠CBD＝180°－30°－105°＝45°，

由正弦定理得＝，

则BC＝＝a(km)，

在△ACD中，∠CAD＝180°－60°－60°＝60°，

所以△ACD为等边三角形．

因为∠ADB＝∠BDC，所以BD为AC的垂直平分线，

所以AB＝BC＝a(km)．

故蓝方这两支精锐部队间的距离为a(km)．

　测量高度问题

【例4】　济南泉城广场上的泉标是隶书“泉”字，其造型流畅别致，成了济南的标志和象征．小明同学想测量泉标的高度，于是他在广场的A点测得泉标顶端的仰角为60°，他又沿着泉标底部方向前进15.2 m，到达B点，又测得泉标顶端的仰角为80°．你能帮小明同学求出泉标的高度吗？ (精确至1 m)

[解]　如图所示，点C，D分别为泉标的底部和顶端．

依题意，得∠BAD＝60°，∠CBD＝80°，AB＝15.2 m，

则∠ABD＝100°，故∠ADB＝180°－(60°＋100°)＝20°．

在△ABD中，根据正弦定理，得＝，

∴BD＝＝≈38.5 m．

在Rt△BCD中，CD＝BDsin 80°≈38.5sin 80°≈38 m．

即泉城广场上泉标的高约为38 m．

1．解决测量高度问题的一般步骤

(1)画图：根据已知条件画出示意图；

(2)分析三角形：分析与问题有关的三角形；

(3)求解：运用正、余弦定理，有序地解相关的三角形，逐步求解．在解题中，要综合运用立体几何知识与平面几何知识，注意方程思想的运用．

2．测量距离问题分为三种类型：两点间不可通又不可视，两点间可视但不可达，两点都不可达．解决此问题的方法是，选择合适的辅助测量点，构造三角形，将问题转化为求某个三角形的边长问题，从而利用正、余弦定理求解．

提醒：解题时要注意题目条件和实际意义中的隐含信息，避免出现增解或漏解．

[跟进训练]

3．如图所示，A，B是水平面上的两个点，相距800 m，在A点测得山顶C的仰角为45°，∠BAD＝120°，∠ABD＝45°，其中D是点C到水平面的垂足，求山高CD．

[解]　因为CD⊥平面ABD，∠CAD＝45°，所以CD＝AD，

因此只需在△ABD中求出AD即可．

在△ABD中，∠BDA＝180°－45°－120°＝15°，

由正弦定理得＝，

所以AD＝＝＝800(＋1)(m)．

即山的高度CD为800(＋1) m．

4．如图，A，B是海面上位于东西方向相距5(3＋)海里的两个观测点，现位于A点北偏东45°，B点北偏西60°的D点有一艘轮船发出求救信号，位于B点南偏西60°且与B点相距20海里的C点的救援船立即前往营救，其航行速度为30海里每小时，该救援船到达D点至少需要几小时？

[解]　由题意知AB＝5(3＋)，∠DBA＝90°－60°＝30°，∠DAB＝45°，所以∠ADB＝105°，

所以sin 105°＝sin 45°cos 60°＋sin 60°cos 45°＝×＋×＝，

在△ABD中，由正弦定理得＝，

所以BD＝＝＝＝10，

又∠DBC＝180°－60°－60°＝60°，BC＝20，

在△DBC中，由余弦定理得

CD2＝BD2＋BC2－2×BD×BCcos 60°

＝300＋1 200－2×10×20×＝900，

所以CD＝30(海里)，则至少需要的时间t＝＝1(小时)．

即该救援船到达D点至少需要1小时．

1．若点A在点C的北偏东60°方向上，点B在点C的南偏东30°方向上，且AC＝BC，则点A在点B的(　　)

A．北偏东15°方向上   B．北偏西15°方向上

C．北偏东10°方向上   D．北偏西10°方向上

A　[由题意，可得几何位置关系如图所示．

则∠CBE＝30°，∠ABC＝45°，所以∠ABE＝15°，故点A在点B的北偏东15°方向上．故选A．]

2．如图，在限速为90 km/h的公路AB旁有一测速站P，已知点P距测速区起点A的距离为0.08 km，距测速区终点B的距离为0.05 km，且∠APB＝60°，现测得某辆汽车从A点行驶到B点所用的时间为3 s，则此车的速度介于(　　)

A．60～70 km/h   B．70～80 km/h

C．80～90 km/h   D．90～100 km/h

C　[由余弦定理得

AB＝＝0.07 km，则此车的速度为×3 600＝7×12＝84 km/h．故选C．]

3．身高相同的甲、乙两人在同一地平面上的不同方向观测20 m高的旗杆，甲观测的仰角为50°，乙观测的仰角为40°，用d1，d2分别表示甲、乙两人离旗杆的距离，那么有(　　)

A．d1>d2   B．d1<d2

C．d1>20 m   D．d2<20 m

B　[如图，设旗杆高为h，

则d1＝，d2＝．

因为tan 50°>tan 40°，

所以d1<d2．

又因为h＝20 m，tan 45°＝1，

所以d1<20 m，d2>20 m，故选C．]

4．一艘船以4 km/h的速度沿着与水流方向成120°的方向航行，已知河水流速为2 km/h，则经过 h，该船实际航程为________ km．

6　[v实＝＝2(km/h)．所以实际航程为2×＝6(km)．]

5．某市在“旧城改造”工程中，计划在如图所示的一块三角形空地上种植草皮以美化环境．已知这种草皮价格为a元/m2，则购买这种草皮需要________元．

150a　[∵S△＝×20×30×sin 150°＝×20×30×＝150(m2)，

∴购买这种草皮需要150a元．]

回顾本节知识，自我完成以下问题：

1．如图，A，B两点在河的对岸，且不可到达，如何测量其两点间的距离？

[提示]　在河岸这边选取点C，D，测得CD＝a，∠ACD＝α，∠BCD＝β，∠BDC＝γ，∠ADC＝δ，则在△ACD和△BCD中应用正弦定理可求AC，BC的长，进而在△ACB中应用余弦定理求AB．

2．如图，如何测量山顶塔AB的高？(测量者的身高忽略不记)

[提示]　测量者在山下先选择一基点P，测出此时山顶的仰角α，前进a米后，再测出此时山顶的仰角β，则借助直角三角形的边角关系可求塔顶距地面的高h，进而利用AB＝h－H求解．